Teorema de Bayes: uma visão interdisciplinar na escola básica
Luciana Gregorio de Morais
Mestranda em Matemática (Profmat/PUC-Rio), especialista em Ensino de Matemática (UFRJ), professora de Matemática naa Seeduc/RJ e de Informática Educativa da Prefeitura de Duque de Caxias/RJ
Christine Sertã Costa
Professora do Departamento de Matemática da PUC-Rio, coordenadora institucional do Profmat/PUC-Rio, professora do Colégio Pedro II
A educação é um caminho essencial para estimular o indivíduo a desenvolver suas habilidades cognitivas de forma esclarecedora e estimulante. Ela contribui para o exercício do questionamento, a formulação de hipóteses e a capacidade de análise, elementos essenciais para uma formação cidadã crítica e autônoma.
Durante o processo de aprendizagem de um conteúdo, os alunos frequentemente levantam questões como: “Mas para que serve isso?”, “Vou usar isso na minha vida?”. Essas indagações, por vezes, resultam da metodologia de ensino aplicada, na qual os saberes são trabalhados de forma fragmentada, e cada disciplina aborda seus temas isoladamente, sem espaço para que os conhecimentos dialoguem entre si.
O ensino interdisciplinar propõe-se a romper com essa prática, buscando interações entre diferentes saberes, que, embora distintos em essência, trazem conceitos que se enriquecem mutuamente quando abordados de forma conjunta. Essas interseções podem ocorrer tanto na aplicação dos conceitos aprendidos em uma disciplina e aplicados em outra, trazendo significado a ambas, quanto no estabelecimento de ferramentas que auxiliem na formulação de estratégias de soluções, especialmente numa abordagem de resolução de problemas.
Dessa forma, a interdisciplinaridade permite que o aluno perceba que o que é aprendido na escola não é apenas aplicável dentro de seus muros nem se limita a processos avaliativos. O aprendizado deve enriquecer o repertório dos estudantes, permitindo-lhe ampliar seu espectro de ferramentas de diferentes disciplinas, que se unem para compor a resolução de situações da vida real e promover um ensino construtivo e integrado. “O ideal da educação não é aprender ao máximo, maximizar os resultados, mas é antes de tudo aprender a aprender, é aprender a se desenvolver e aprender a continuar a se desenvolver depois da escola” (Piaget, 1972, p. 32).
O ensino interdisciplinar, aliado à resolução de problemas, proporciona ao alunado uma educação integrada através da interação de diversos saberes e construtiva, na medida em que, para alcançar a resolução de um problema, o aluno percorre um processo em que assimila as informações fornecidas, reflete sobre situações, formula estratégias e as aplica para resolver problemas.
Um ensino integrado percorre diversas áreas do conhecimento em busca de ferramentas de diferentes naturezas, construindo um processo de ensino-aprendizagem mais sólido e enriquecedor. Um caminho que pode levar ao ensino baseado na construção de saberes é aquele que estimula o aluno a refletir e a buscar soluções, formulando questionamentos e pesquisando possíveis respostas. O ensino interdisciplinar e a resolução de problemas, portanto, incentivam um ensino significativo, visando ao despertar da autonomia dos alunos na construção de um conhecimento amplo e construtivo.
A habilidade de relacionar e integrar diferentes saberes pode ser desenvolvida mediante um processo de ensino que, desde cedo, valorize a inserção da interdisciplinaridade e da resolução de problemas no contexto escolar. É com esse olhar que este artigo se constrói, procurando refletir sobre a interdisciplinaridade a partir da proposta de problemas a serem resolvidos, neste caso, utilizando o teorema de Bayes como conceito matemático a ser trabalhado. Esse teorema faz parte do currículo de Matemática do Ensino Médio da Educação Básica e, em geral, constitui um estudo probabilístico de difícil compreensão por parte do alunado.
A prática interdisciplinar e a resolução de problemas
A interdisciplinaridade tem sido amplamente discutida por diversos autores, como Pombo (2005), Furegato e Gattás (2006), Thiesen (2008), Frigotto (2008) e Fazenda (2015). Esses referenciais teóricos apontam o trabalho interdisciplinar como facilitador na integração entre disciplinas e no compartilhamento de saberes, estimulando, assim, uma educação mais participativa e colaborativa entre diferentes áreas do conhecimento.
Ao trabalhar conceitos em conjunto com duas ou mais disciplinas, espera-se o entrosamento e o diálogo entre elas. Esse intercâmbio de informações enriquece as disciplinas envolvidas, preservando suas essências, tornando-as ferramentas relevantes para a construção de um conhecimento mais amplo e coletivo. Fazenda (2015) destaca a importância de estar constantemente atento ao desenvolvimento do conhecimento:
O conceito de interdisciplinaridade como ensaiamos em todos nossos escritos desde 1979 e agora aprofundamos encontra-se diretamente ligado ao conceito de disciplina, onde a interpenetração ocorre sem a destruição básica às ciências conferidos (sic). Não se pode de forma alguma negar a evolução do conhecimento ignorando sua história (Fazenda, 2015, p. 12).
Embora a interdisciplinaridade seja muito discutida atualmente, corroboramos as ideias de Thiesen (2008), que destaca ser fundamental defender a inserção da interdisciplinaridade no contexto escolar, já que ainda se observa certa resistência em aplicá-la em algumas instituições de ensino:
Embora a temática da interdisciplinaridade esteja em debate tanto nas agências formadoras quanto nas escolas, sobretudo nas discussões sobre projeto político-pedagógico, os desafios para a superação do referencial dicotomizador e parcelado na reconstrução e socialização do conhecimento que orienta a prática dos educadores ainda são enormes (Thiesen, 2008, p. 550).
Essa resistência pode decorrer da preocupação e da insegurança de alguns profissionais de ensino de abordar temas de disciplinas fora de seu campo de formação. No entanto, a interdisciplinaridade também beneficia a formação continuada dos professores, que passam a ter a oportunidade de expandir seus conhecimentos e ultrapassar possíveis barreiras que os isolam em seus campos de atuação.
Um dos requisitos primordiais no ensino interdisciplinar é que o corpo docente se comprometa a desenvolver conceitos de forma interdisciplinar, trabalhe em parceria contínua, promovendo apoios e incentivos, e compartilhe experiências e saberes em busca de um ensino dialógico, integrado e significativo. Furegato e Gattás (2006) destacam que a
interdisciplinaridade pode ser entendida como qualquer forma de combinação entre duas ou mais disciplinas objetivando-se a compreensão de um objeto a partir da confluência de pontos de vista diferentes cujo objetivo final seria a elaboração de síntese relativa ao objeto comum; implica alguma reorganização do processo ensino/aprendizagem e supõe trabalho contínuo de cooperação entre os professores envolvidos (Furegato; Gattás, 2006, p. 325).
Dado que esse tema é amplamente difundido no meio pedagógico, especialmente na escola básica, e sua prática é incentivada, é importante que se tenha clareza e cuidado para não transformar a interdisciplinaridade em um modismo, assegurando sempre sua intencionalidade e planejamento. Pombo (2005) ressalta que é essencial haver real comprometimento no processo de promoção do ensino interdisciplinar e dedicação para alcançar efetivamente os objetivos pedagógicos traçados:
O que significa que, assim sendo, a interdisciplinaridade não é qualquer coisa que nós tenhamos que fazer. É qualquer coisa que se está a fazer quer nós queiramos ou não. Nós estamos colocados numa situação de transição e os nossos projectos particulares não são mais do que formas, mais ou menos conscientes, de inscrição nesse movimento (Pombo, 2005, p. 10).
Na sociedade atual, com o avanço das tecnologias e o constante fluxo de informações, a interdisciplinaridade emerge como instrumento para a capacitação simultânea de diferentes saberes, com os quais usualmente nos deparamos em diversas situações cotidianas. Ela pode ir além das barreiras que frequentemente separam as disciplinas escolares, atendendo às necessidades práticas da sociedade contemporânea. Frigotto (2008) enfatiza:
O caráter necessário do trabalho interdisciplinar na produção e na socialização do conhecimento no campo das ciências sociais e no campo educativo que se desenvolve no seu bojo, não decorre de uma arbitrariedade racional e abstrata. Decorre da própria forma do homem produzir-se enquanto ser social e enquanto sujeito e objeto do conhecimento social (Frigotto, 2008, p. 43).
Os autores citados defendem o ensino interdisciplinar com o intuito de promover a interação entre saberes e proporcionar ao aluno um conhecimento mais amplo e significativo. Esse conhecimento em construção possivelmente encontrará, ao longo do processo, um importante aliado: o ensino por meio da resolução de problemas. Com essa metodologia, o aluno pode visualizar o que aprende inserido em contextos próximos à sua realidade, atribuindo sentido ao aprendizado.
Polya (1945) dividiu o processo de resolução de um problema em quatro etapas: compreensão do problema, construção de uma estratégia de resolução para o problema, execução dessa estratégia e revisão da solução. Segundo o autor, a aprendizagem se torna mais construtiva à medida que o aluno reflete sobre um problema e busca uma solução para sua superação, desenvolvendo sua autonomia e adquirindo um conhecimento mais profundo:
Uma grande descoberta resolve um grande problema, mas há sempre uma pitada de descoberta na resolução de qualquer problema. O problema pode ser modesto, mas se ele desafiar a curiosidade e puser em jogo as faculdades inventivas, quem o resolver por seus próprios meios, experimentará a tensão e gozará o triunfo da descoberta. Experiências tais, numa idade susceptível, poderão gerar o gosto pelo trabalho mental e deixar, por toda a vida, a sua marca na mente e no caráter (Polya, 1995, p. V).
Por meio da interdisciplinaridade e da resolução de problemas, os alunos, além de relacionarem diferentes saberes em busca de um objetivo comum, desenvolverão habilidades de observação, reflexão, síntese e elaboração de estratégias para resolver situações-problema propostas pelo professor durante o processo de ensino-aprendizagem. Assim, proporciona-se ao alunado uma formação que estimula o pensamento e a busca por estratégias de solução, desenvolvendo sua autonomia e conferindo significado a todo o processo.
Nas próximas seções, apresentamos o Teorema de Bayes e propomos a resolução de um problema com o intuito de, na busca de uma estratégia para sua solução, utilizar o teorema promovendo um diálogo entre a abordagem interdisciplinar e outras ciências, fundamentando o ensino por meio da resolução de problemas.
O Teorema de Bayes
O Teorema de Bayes é um teorema amplamente difundido no campo da Matemática, com aplicação em várias outras áreas do conhecimento. Ele recebeu esse nome em homenagem a Thomas Bayes, um pastor presbiteriano e matemático inglês do século XVIII. Bayes escreveu o Ensaio para resolver um problema na doutrina das chances, mas foi Richard Price, filósofo, ministro da igreja dissidente da Inglaterra e político republicano liberal, que enviou o documento à Royal Society após o falecimento de Bayes. Nesse documento encontra-se o referido teorema, que considera dois eventos dependentes e apresenta uma expressão matemática para calcular a probabilidade de um evento ocorrer sabendo-se da ocorrência prévia do outro.
Dessa forma, considerando que:
- A e B são eventos dependentes, ou seja, a ocorrência de um evento afeta a probabilidade de ocorrência do outro evento;
- P(A) e P(B) são as probabilidades a priori de A e B;
- P(B) ≠ 0;
- P(A│B) é a probabilidade a posteriori de A condicional a B, ou seja, a probabilidade de A ocorrer, dado que B já ocorreu (a probabilidade do evento A ocorrer é calculada ao se levar em consideração a ocorrência prévia do evento B);
- P(B│A) é a probabilidade a posteriori de B condicional a A, ou seja, a probabilidade de B ocorrer, dado que A já ocorreu;
- P(B) = P(B│A) P(A) + P(B│~A) P(~A) (Teorema da Probabilidade Total, onde ~A significa não ocorrer o evento A).
A expressão matemática que descreve o Teorema de Bayes é:
P(A│B) = 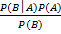
Como mencionamos neste texto, o Teorema de Bayes é usualmente apresentado nas aulas de Matemática do Ensino Médio, mas possui aplicabilidade em várias ciências. Seu estudo com enfoque interdisciplinar contribui não apenas para o conhecimento específico do tema, mas também para ampliar o espectro de conhecimento geral do aluno e o aprendizado de dinâmicas de resolução de problemas. Ele costuma ser empregado em situações em que a probabilidade de um evento ocorrer é afetada pela ocorrência prévia de outro evento.
Cabe destacar que esse teorema é uma importante ferramenta no campo probabilístico, contribuindo para diversas áreas do conhecimento ao considerar a atualização das probabilidades a serem calculadas diante da ocorrência de acontecimentos prévios. Nas ciências médicas, por exemplo, “a abordagem bayesiana tem ampla aplicação em processos diagnósticos, inclusive na construção de sistemas especialistas, sendo bem conhecida na literatura científica” (Massad, 2011, p. 10).
Considerando as ciências da informação e da computação, a BBC News Brasil (2021) relata que o uso do teorema revolucionou o estudo do Universo, e que o empresário Bill Gates credita ao trabalho de Bayes parte do sucesso da Microsoft.
Algoritmos que usam o Teorema de Bayes, hoje, podem produzir previsões mais acuradas em diferentes campos como: a criação de vacinas, tradução de idiomas estrangeiros, predição de crimes, investigações sobre doenças, quebra de senhas, análise de discursos, busca por novos planetas, busca e resgate em acidentes ocorridos em áreas remotas etc. (Reis, 2022).
Propor atividades que apliquem o teorema em situações práticas e reais confere significado ao que está sendo aprendido, amplia o conhecimento sobre outras ciências e motiva os alunos. Com o intuito de apresentar uma proposta que dialogue com as reflexões desenvolvidas até o momento, elaboramos uma atividade que utiliza o Teorema de Bayes na resolução de um problema que integra saberes de diversas ciências. A próxima seção detalha essa construção.
Aplicação do Teorema de Bayes em uma abordagem interdisciplinar com a Astronomia, a História e a Geografia
A Matemática, a Astronomia, a História e a Geografia são ciências que há muito tempo contribuem para o desenvolvimento da humanidade. A Base Nacional Comum Curricular (BNCC) (Brasil, 2018) inclui Matemática, História e Geografia diretamente no currículo escolar da Educação Básica, por meio das áreas do conhecimento Matemática e Ciências Humanas. A Astronomia, por sua vez, está presente no documento por meio de alguns conteúdos abordados na disciplina de Ciências, na área de Ciências da Natureza. Um dos estudos dessa área envolve o estudo das constelações, e é nesse tópico que nossa proposta interdisciplinar se insere.
Texto explicativo com abordagem interdisciplinar
As constelações são agrupamentos aparentes de estrelas. Oficialmente, a União Astronômica Internacional (UAI) reconhece 88 constelações no céu. Dentre elas, existem treze chamadas de constelações do zodíaco. Por meio da Astronomia, é possível determinar o aspecto do céu em uma data e local específicos. Algumas das constelações visíveis no céu em 15 de novembro de 1889, data da Proclamação da República, foram escolhidas para compor a Bandeira Nacional, o que referenda a importância desse estudo.
A bandeira brasileira atual foi concebida logo após a Proclamação da República, e as 27 estrelas representadas nela formam nove constelações, algumas completas e outras parciais: Cão Menor (1), Cão Maior (2), Quilha (3), Hidra Fêmea (5), Cruzeiro do Sul (6), Oitante (7), Triângulo Austral (8), além de duas constelações: Escorpião (9) e Virgem (4).
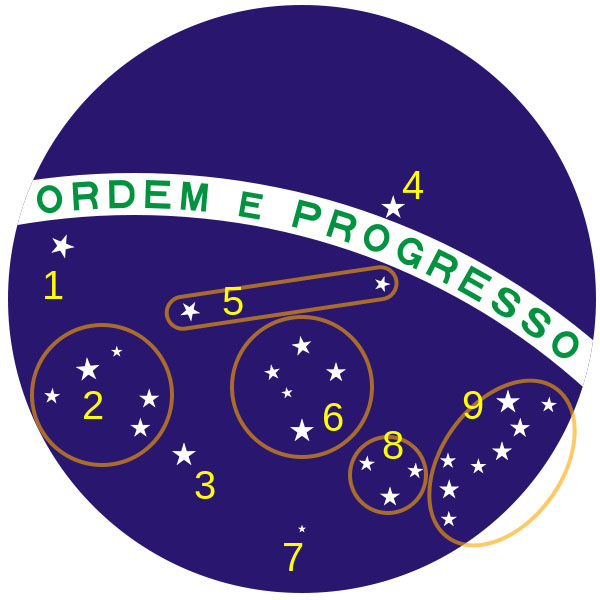
Figura 1: Constelações representadas na bandeira do Brasil
Fonte: Galeria do Meteorito.
Problema proposto
Para uma apresentação de seminário, ficou decidido que cada aluno de uma turma falaria sobre uma constelação. Para garantir que as apresentações fossem sobre constelações distintas, foi organizado um sorteio para definir a constelação de cada aluno. A professora escreveu o nome de cada constelação reconhecida pela UAI em papéis separados e os colocou em uma urna. A dinâmica do sorteio seria realizada da seguinte forma: cada aluno, respeitando a ordem de chamada na turma, deveria retirar um papel da urna sem ler o nome da constelação sorteada. O papel seria entregue à professora, que anotaria a constelação de cada aluno e só revelaria as atribuições ao final do processo.
O primeiro aluno retirou o seu papel e entregou-o à professora.
1° questionamento: Qual a probabilidade de a constelação retirada pelo primeiro aluno ser uma constelação do zodíaco?
Solução sugerida: Existem oficialmente 88 constelações no universo, 13 delas chamadas constelações zodiacais. Assim, a chance de que o papel retirado pelo primeiro aluno contenha o nome de uma constelação zodiacal é de 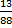 .
.
2° questionamento: Qual a probabilidade de a constelação retirada pelo 1º aluno ser do zodíaco, sabendo que a professora comunicou à turma que a constelação retirada está presente na bandeira do Brasil?
Solução usando o Teorema de Bayes:
Considere os eventos:
A: constelação retirada ser do zodíaco
~A: constelação retirada não ser do zodíaco
B: constelação retirada está na bandeira do Brasil
Assim:
P(A) é a probabilidade de a constelação retirada ser do zodíaco
P(~A) é a probabilidade de a constelação retirada não ser do zodíaco
P(B) é a probabilidade de a constelação retirada estar na bandeira do Brasil
P(A│B) é a probabilidade de a constelação retirada ser do zodíaco, sabendo que ela está na bandeira do Brasil
P(B│A) é a probabilidade de a constelação retirada estar na bandeira do Brasil, sabendo que é uma constelação do zodíaco
P(B│~A) é a probabilidade de a constelação retirada estar na bandeira do Brasil, sabendo que ela não é uma constelação do zodíaco
Nessas condições tem-se:
P(A│B) =
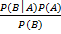 =
=
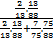 =
=
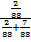 =
=
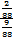 =
=

Outra solução: Com a informação de que a constelação está presente na bandeira do Brasil, o espaço amostral reduz-se para nove constelações. Logo, a probabilidade de que a constelação seja zodiacal é  .
.
3° questionamento: Continuando o processo de sorteio, qual a probabilidade de o 2º aluno retirar uma constelação zodiacal que consta na bandeira do Brasil, sabendo que o 1º aluno já retirou uma constelação zodiacal da bandeira?
Solução usando o Teorema de Bayes:
Considere os eventos:
A: retirar uma constelação zodiacal que consta na bandeira do Brasil
~A: não retirar uma constelação zodiacal que consta na bandeira do Brasil
B: retirar uma constelação zodiacal da bandeira do Brasil
Assim:
P(A) é a probabilidade de retirar uma constelação zodiacal que consta na bandeira do Brasil
P(~A) é a probabilidade de não retirar uma constelação zodiacal que consta na bandeira do Brasil
P(B) é a probabilidade de retirar uma constelação zodiacal da bandeira do Brasil
P(A│B) é a probabilidade de o 2º aluno retirar uma constelação zodiacal que consta na bandeira do Brasil, sabendo que o 1º aluno retirou uma constelação zodiacal da bandeira
P(B│A) é a probabilidade de o 1º aluno ter retirado uma constelação zodiacal da bandeira do Brasil, sabendo que o 2º aluno retirou uma constelação zodiacal que consta na bandeira do Brasil
P(B│~A) é a probabilidade de o 1º aluno ter retirado uma constelação zodiacal da bandeira do Brasil, sabendo que o 2º aluno não retirou uma constelação zodiacal que consta na bandeira do Brasil
Nessas condições, tem-se:
P(A│B) = 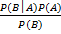 =
=
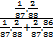 =
=
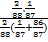 =
=
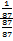 =
=
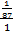 =
=
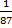
Outra solução: Após o 1º aluno retirar uma constelação, o espaço amostral reduz-se para 87 constelações. Sabendo que uma das duas constelações zodiacais da bandeira brasileira foi retirada, resta apenas uma delas para ser sorteada pelo 2º aluno. Logo, a probabilidade de o 2º aluno retirar uma constelação zodiacal que consta na bandeira do Brasil é 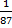 .
.
Esse exemplo demonstra como novas informações alteram o espaço amostral e, consequentemente, as probabilidades. Esse é basicamente o princípio do Teorema de Bayes: ao calcular a probabilidade a posteriori, vemos que, ao reduzir o espaço amostral e calcular a probabilidade aplicando o método clássico, chegamos ao mesmo resultado obtido pela aplicação do teorema de Bayes. Assim, podemos perceber que, muitas vezes, utilizamos intuitivamente a lógica do teorema, o que o torna sua aplicação muito útil em cálculos mais complexos. Dessa forma, o teorema foi apresentado de forma contextualizada, integrando conhecimentos de diferentes áreas e praticando a interdisciplinaridade entre saberes.
Considerações finais
A prática interdisciplinar no ambiente escolar, dentro do processo de ensino-aprendizagem, pode contribuir para uma educação mais sólida e significativa, na qual os alunos utilizem e desenvolvam diversos saberes simultaneamente. Muitos estudantes podem demonstrar maior envolvimento em uma dinâmica de ensino que ofereça uma educação mais integrada e conectada a situações cotidianas, abordando temas relevantes para suas realidades ou comuns à sociedade em geral. Esse tipo de abordagem pode contribuir para o esclarecimento de questionamentos recorrentes dos alunos sobre a utilidade e a importância dos conteúdos ensinados, ampliando sua compreensão sobre a aplicabilidade desses conhecimentos em diferentes contextos e áreas do saber. A interdisciplinaridade entre saberes torna-se, portanto, uma facilitadora para um ensino que ofereça ao aluno um conhecimento duradouro e uma formação sólida para a vida.
Ao aplicar o Teorema de Bayes em outras áreas científicas, percebe-se que o ensino das ciências não precisa ser fragmentado. As ciências, afinal, buscam o bem da sociedade e, nesse sentido, a apresentação de interações entre diferentes áreas do conhecimento torna-se uma poderosa aliada para o enriquecimento de diversos saberes e na busca pela solução de questões e de resolução de situações, alcançando, assim, um conhecimento construtivo e integrado.
Referências
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília: MEC, 2018.
CASTRO, Leonardo; RIBEIRO, Rafaela; ALVES, Renata. A Astronomia e a história da bandeira do Brasil. Invivo Museu da Vida, 2023. Disponível em: https://www.invivo.fiocruz.br/cienciaetecnologia/a-astronomia-e-a-historia-da-bandeira-do-brasil/. Acesso em: 5 dez. 2023.
FAZENDA, Ivani. Interdisciplinaridade. Revista do Grupo de Estudos e Pesquisa em Interdisciplinaridade, p. 9-17, 2015.
FRIGOTTO, Gaudêncio. A interdisciplinaridade como necessidade e como problema nas Ciências Sociais. Revista do Centro de Educação e Letras da Unioeste - Foz do Iguaçu, v. 10, nº 1, p. 41-62, jan./jun. 2008.
FUREGATO, Antonia Regina; GATTÁS, Maria Lucia. Interdisciplinaridade: uma contextualização. Acta Paulista de Enfermagem, v. 19, p. 323-327, 2006.
GALERIA DO METEORITO. Qual é o significado das estrelas da bandeira do Brasil? s/d. Disponível em: https://www.galeriadometeorito.com/2018/07/qual-significado-das-estrelas-bandeira-brasil.html. Acesso em: 5 dez. 2023.
MASSAD, Eduardo. Surge um novo conceito de doença e de saúde. Tratamento das incertezas em medicina. A lógica fuzzy pode contribuir muito com áreas em que é necessário lidar com a subjetividade e o desconhecimento. Revista Ser Médico, São Paulo, nº 55, p. 10, abr./jun. 2011.
O QUE É O TEOREMA DE BAYES, regra essencial da informática criada para “provar milagres”. BBC News Brasil, São Paulo, 2021. Disponível em: https://www.bbc.com/portuguese/internacional-59701523. Acesso em: 26 out. 2023.
PENA, Sérgio Danilo. Thomas Bayes: o ‘cara’! Ciência Hoje, v. 38, nº 228, 2006.
PIAGET, Jean. O tempo e o desenvolvimento intelectual da criança. In: PIAGET, Jean. Problemas de Psicologia Genética. Rio de Janeiro: Forense, 1972.
POLYA, G. How to solve it: a new aspect of mathematical method. Princeton: Princeton University Press, 1945.
POLYA, G. A arte de resolver problemas: um novo aspecto do método matemático. Trad. e adapt. Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 1995.
POMBO, Olga. Interdisciplinaridade e integração dos saberes. Liinc em Revista, v. 1, nº 1, p. 3-15, mar. 2005.
REIS, Nazareno César. Fé, probabilidade e IA: o Teorema de Bayes. PhiloTechJus, 2022.
THIESEN, Juares. A interdisciplinaridade como um movimento articulador no processo ensino-aprendizagem. Revista Brasileira de Educação, v. 13, nº 39, p. 545-554, set./dez. 2008.
UNIÃO ASTRONÔMICA INTERNACIONAL (UAI). As constelações. 3 set. 2018. Disponível em: https://www.iau.org/public/themes/constellations/brazilian-portuguese/. Acesso em: 27 out. 2023.
Publicado em 17 de dezembro de 2024
Como citar este artigo (ABNT)
MORAIS, Luciana Gregorio de; COSTA, Christine Sertã. Teorema de Bayes: uma visão interdisciplinar na escola básica. Revista Educação Pública, Rio de Janeiro, v. 24, nº 46, 17 de dezembro de 2024. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/24/46/teorema-de-bayes-uma-visao-interdisciplinar-na-escola-basica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
2 Comentários sobre este artigo
Deixe seu comentárioMuito interessante. Onde menos se imagina, há Matemática!
Excelente material! Parabéns aos autores.
Este artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

