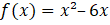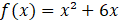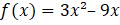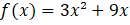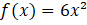Funções quadráticas e o jogo Angry Birds Friends
Augusto de Almeida Barros Soares
Licenciando em Matemática (Uneal - câmpus III - Palmeira dos Índios)
Jamily Leite Máximo
Licencianda em Matemática (Uneal - câmpus III - Palmeira dos Índios)
Moizeis Veiga Ferreira
Licenciando em Matemática (Uneal - câmpus III - Palmeira dos Índios)
Rayane de França da Silva
Licencianda em Matemática (Uneal - câmpus III - Palmeira dos Índios)
Tácio Barros da Silva
Licenciando em Matemática (Uneal - câmpus III - Palmeira dos Índios)
João Ferreira da Silva Neto
Docente do curso de Licenciatura em Matemática (Uneal - câmpus III - Palmeira dos Índios), doutor em Educação (UFRGS)
Este trabalho se insere na problemática mais ampla do uso de jogos no ensino e na aprendizagem de Matemática, tratando da descrição de uma sequência didática para o estudo de funções quadráticas, com a utilização da gamificação. Alves, Carneiro e Carneiro (2022) discutem a possibilidade de se utilizar as tecnologias digitais para o desenvolvimento do ensino da Matemática em sala de aula. Nesse contexto, a abordagem gamificada tem surgido como uma estratégia promissora para tornar o aprendizado de Matemática mais atrativo e prático.
Andrade (2017) apresenta reflexões sobre as dificuldades que os alunos enfrentam na compreensão de funções quadráticas, destacando a abordagem estática com que esse conceito é tradicionalmente ensinado. Diante disso, acreditamos que é de extrema relevância refletir e elaborar atividades que possam contribuir para a aprendizagem dos conceitos matemáticos, incluindo o conceito de função quadrática.
Nessa perspectiva, desenvolvemos a sequência didática Funções Quadráticas e o Jogo Angry Birds Friends, planejada para turmas do terceiro ano do Ensino Médio em uma escola pública estadual de Alagoas. Essa proposta foi concebida e aplicada como parte das atividades da disciplina Laboratório de Ensino Matemático II, do Curso de Licenciatura em Matemática da Universidade Estadual de Alagoas (Uneal).
Além disso, como bolsistas do Programa Residência Pedagógica (PRP/Capes), aproveitamos o módulo de regência para explorar o ensino de funções quadráticas por meio de uma abordagem gamificada, utilizando o jogo Angry Birds Friends. A trajetória dos personagens do jogo, aliada ao uso do software GeoGebra, possibilitou um estudo dinâmico e interativo do tema. O uso do jogo se mostrou um fator motivador para os alunos, pois a combinação entre gamificação e ensino de Matemática despertou maior interesse na aprendizagem dos conceitos abordados
As metodologias ativas, como a gamificação, e o uso de tecnologias digitais "contribuem para a dinamização da sala de aula, permitindo a integração de novos saberes, muitos deles presentes em nosso cotidiano" (Vasconcelos; Andrade; Negrão, 2020, p. 446). Como destacam esses autores, as tecnologias digitais da informação e comunicação (TDIC) desempenham papel fundamental na ressignificação do ensino e da aprendizagem de conceitos matemáticos.
O jogo Angry Birds Friends se baseia em princípios físicos de movimento, desafiando os jogadores a lançar pássaros com estilingues para derrubar estruturas e derrotar porcos verdes. Freitas e Neto (2018) ressaltam que, além de sua popularidade e sua simplicidade, o jogo possibilita experiências semelhantes a situações do cotidiano, especialmente no que diz respeito à trajetória de objetos lançados. Diante disso, Angry Birds Friends foi escolhido para a elaboração da sequência didática devido à sua acessibilidade — sendo um jogo multiplataforma — e à presença de trajetórias parabólicas, que representam graficamente as funções quadráticas.
Antes de descrever a situação didática desenvolvida, é pertinente discutir a relevância de atividades significativas para os alunos. A seguir, apresentamos o relato da experiência, analisando como essa abordagem gamificada impactou o processo de aprendizagem.
Jogos e aprendizagem matemática
Lima e Negrão (2022) ressaltam que o uso de jogos facilita os processos de ensino e aprendizagem. Para esses autores, objetos eletrônicos podem ser utilizados como estratégias para desenvolver o conhecimento matemático dos alunos, visto que, especialmente na Matemática, os alunos enfrentam dificuldades de interpretação e de raciocínio lógico, oriundas do processo de alfabetização.
Esses autores acrescentam que o uso dos jogos eletrônicos, ao mesmo tempo que incorporam as experiências cotidianas dos alunos, ampliam o potencial de estabelecer a correlação dessas experiências com os conteúdos matemáticos. Com isso, esses recursos se apresentam como ferramentas valiosas no desenvolvimento de atividades escolares, pois estimulam o raciocínio ao despertar maior atenção dos alunos.
Baumgartel (2016) afirma que os jogos podem ser utilizados para o desenvolvimento de habilidades e aprendizagem no processo de ensino, uma vez que possuem regras a serem seguidas, o que permite a introdução de conceitos para a realização de procedimentos em sala de aula. Nessa linha de pensamento, Silva (2022) vê o jogo como uma oportunidade para que o aluno troque experiências e fortaleça sua capacidade de decisão.
Assim, os jogos podem ser aproveitados pela escola como uma metodologia de ensino, principalmente para amenizar as dificuldades de contextualização dos conteúdos matemáticos. Nesse sentido, o estudo de Moita et al. (2013) afirma que a escola vem utilizando recursos tecnológicos, como jogos analógicos e eletrônicos, com o objetivo de aproximar os conteúdos estudados na escola do cotidiano do aluno.
O uso de jogos no ensino está diretamente relacionado ao conceito de gamificação. No entanto, como ressalta Alves (2015), gamificar não significa simplesmente transformar uma atividade em um jogo, mas sim identificar e incorporar os elementos mais eficazes dos jogos para enriquecer outras experiências, sem necessariamente convertê-las integralmente em jogos.
Nesse sentido, a adoção de jogos em programas educacionais e de treinamento busca potencializar o engajamento dos participantes e facilitar o processo de aprendizagem. Como enfatiza Alves (2015, p. 30), é essencial “encontrar elementos dos games que podem melhorar uma experiência sem desprezar o mundo real. Encontrar o conceito central de uma experiência e torná-la mais divertida e engajadora” (Alves, 2015, p. 30).
Metodologia
O processo metodológico para a elaboração e aplicação da sequência didática descrita foi desenvolvido no âmbito do componente curricular Laboratório de Ensino de Matemática II e esteve constantemente articulado às atividades do Programa Residência Pedagógica (PRP/Capes/Uneal). A proposta teve como foco o estudo das funções quadráticas, adotando uma abordagem gamificada por meio do jogo Angry Birds Friends, a fim de tornar a aprendizagem mais interativa e significativa para os alunos.
Escolhemos esse jogo devido à sua capacidade de ilustrar situações que delineiam as trajetórias de projéteis lançados, proporcionando uma representação visual das parábolas estudadas nas funções quadráticas. Além disso, selecionamos a versão do jogo levando em consideração, conforme ressaltam Freitas e Neto (2018), sua popularidade, sua simplicidade e sua capacidade de simular situações cotidianas.
Para esclarecer a sequência didática desenvolvida e analisada, optamos por descrevê-la em cinco momentos distintos. Como ponto de partida, a apresentação do jogo foi realizada, detalhando o funcionamento do jogo. Propusemos que um aluno voluntário participasse jogando uma partida no computador, projetada na tela de uma TV na sala de aula. Essa abordagem possibilitou que todos na sala observassem a trajetória parabólica executada pelos personagens do jogo.
No segundo momento, um problema inicial envolvendo uma partida do jogo Angry Birds Friends foi proposto aos alunos. Para resolvê-lo, os alunos precisavam analisar a trajetória realizada pelo personagem em relação a um plano cartesiano exibido ao fundo da figura. Esse problema foi proposto com o objetivo de contribuir para o entendimento dos conceitos de vértice e raízes da função quadrática. A Figura 1 apresenta o problema inicial proposto.

Figura 1: Problema inicial utilizando um recorte do jogo Angry Birds Friends
Após o jogo, iniciamos uma contextualização histórica do estudo da função quadrática, acompanhada por uma discussão sobre situações cotidianas e objetos nos quais a presença de parábolas poderia ser identificada. Exemplificamos essa relação com o formato de certas pontes, instrumentos musicais e antenas parabólicas. Além disso, discutimos situações que envolvem o lançamento de objetos diversos, incentivando a reflexão sobre outras instâncias em que as trajetórias parabólicas podem ser observadas em nosso ambiente.
No terceiro momento, os alunos exploraram os termos da fórmula geral da função quadrática e as implicações advindas de suas variações, analisando tanto as trajetórias parabólicas dos personagens do jogo quanto os gráficos gerados no aplicativo GeoGebra. O uso desse software permitiu uma representação visual mais clara dos conceitos abordados, facilitando a compreensão das propriedades das funções quadráticas. Amancio e Sanzovo (2020) destacam que os softwares de Geometria Dinâmica, como o GeoGebra, desempenham papel fundamental na aprendizagem, tornando as aulas mais interativas e atrativas, além de proporcionar maior dinamismo ao ensino da Matemática.
Para ilustrar as implicações da variação do coeficiente "a", optamos por integrar imagens do jogo, sobrepostas por um plano cartesiano no GeoGebra, conforme apresentado na Figura 2.

Figura 2: Apresentação do coeficiente “a” da função utilizando um recorte do jogo Angry Birds Friends
Utilizando as situações do jogo, foi possível modelar parábolas mais longas ou mais estreitas para explicar o que ocorre graficamente em relação ao valor absoluto de "a". Além disso, para exemplificar a parábola com concavidade voltada para cima, recorremos a uma imagem espelhada e invertida de uma partida do Angry Birds Friends, contrastando com a parábola de concavidade voltada para baixo, comumente encontrada nesse jogo. Ao utilizar o jogo para abordar o estudo desse coeficiente, o objetivo foi ampliar as possibilidades de assimilação das parábolas que exibem esse coeficiente como negativo, uma vez que essas são as únicas trajetórias apresentadas no contexto do jogo.
Em relação ao coeficiente "b", deslocamos as capturas de tela do jogo para ambos os lados, em relação à origem do plano cartesiano do GeoGebra, caracterizando o deslocamento horizontal, conforme apresentado na Figura 3. O deslocamento vertical, ao variar o coeficiente "c", seguiu de forma análoga nas capturas de tela, como mostrado na Figura 4.

Figura 3: Apresentação do coeficiente “b” da função utilizando um recorte do jogo Angry Birds Friends

Figura 4: Apresentação do coeficiente “c” da função utilizando um recorte do jogo Angry Birds Friends
Como complemento à explicação sobre as funções quadráticas, utilizamos o software GeoGebra para construir uma parábola a partir da fórmula geral e procedemos à variação de cada coeficiente. Essa abordagem gráfica teve como objetivo contemplar as implicações das variações dos coeficientes, transcendendo o contexto do jogo. Ao variarmos diretamente os coeficientes, os alunos puderam observar de forma dinâmica como cada parâmetro afeta a forma e a orientação da parábola.
No quarto momento, utilizando não só recortes de partidas do jogo Angry Birds Friends, mas também representações gráficas de parábolas construídas no GeoGebra, discutimos a maior altura que o personagem do jogo alcançava a cada lançamento. Essa discussão visou a definição dos conceitos de máximo e de mínimo das funções, incluindo a explicitação do vértice da parábola. Integrando as construções previamente mencionadas e utilizando o jogo como recurso, exploramos as fórmulas para calcular as raízes das funções quadráticas e o vértice da parábola, ponto de mínimo ou de máximo. Esses conceitos foram abordados no material da sequência didática, abrangendo a formalidade matemática inerente ao estudo das funções quadráticas.
Ao término da sequência didática, sugerimos aos alunos a resolução de três exercícios para fixar o conteúdo estudado, conforme ilustrado no Quadro 1.
Quadro 1: Exercícios abordados no decorrer do material de aula
Exercícios |
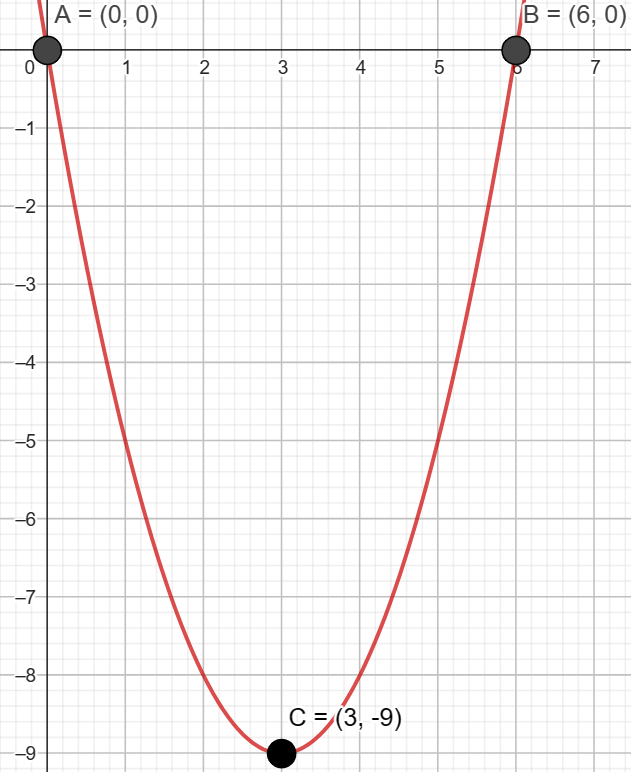
Exercício 1: Esboce o gráfico da seguinte função:
|
Exercício 2: Considere a função definida por
a) Determine os zeros de
b) Calcule as coordenadas do vértice de seu gráfico. c) Esboce seu gráfico. |
Exercício 3 (Saepe): Observe ao lado o gráfico da função quadrática definida de
(A) (B) (C) (D) (E)
|
Em última instância, com a correção dos exemplos apresentados, incluindo o problema inicial, foi distribuída uma lista de exercícios. Essa lista foi composta por dez questões de múltipla escolha que abordavam os conceitos estudados, com foco nas aplicações e na representação gráfica da função quadrática.
As questões da lista envolviam a análise dos vértices das parábolas, explorando como localizar suas coordenadas e entender as implicações das alterações dos coeficientes no comportamento dos gráficos. Além disso, a tarefa incluiu questões em que os alunos precisavam substituir valores específicos de x na função para encontrar o valor de y e identificar os pontos de máximo e de mínimo, proporcionando uma visão abrangente das propriedades características das parábolas. Essa etapa foi planejada com o intuito de validar a eficácia da abordagem utilizada, oferecendo aos alunos a oportunidade de aplicar os conhecimentos adquiridos e consolidar sua compreensão por meio da prática.
Resultados e discussão
A utilização do Angry Birds Friends como recurso gamificado proporcionou uma introdução envolvente e atrativa para os alunos, alinhando-se às ideias de Alves (2015). A familiaridade prévia com o jogo gerou entusiasmo entre os estudantes, favorecendo sua participação ativa.
No entanto, ao propor a resolução do problema inicial, observou-se que os alunos não direcionaram sua atenção para a função matemática que representava a parábola descrita no enunciado. Em vez disso, concentraram-se em uma abordagem mais intuitiva, limitando-se à análise visual da imagem, sem considerar a relação matemática subjacente ao movimento representado.
No contexto das aplicações das parábolas no cotidiano, durante a discussão em sala de aula, os alunos identificaram diversos exemplos, como a trajetória de uma bolinha de papel lançada ao ar e o formato da aba de um boné. Essas associações espontâneas demonstram a capacidade dos estudantes de relacionar os conceitos matemáticos com situações do dia a dia, favorecendo uma compreensão mais concreta e significativa do tema.
Como a sequência didática proposta visava revisar funções quadráticas, um conceito matemático estudado em séries anteriores, os alunos relacionaram o estudo da fórmula geral da função quadrática ao estudo da função do primeiro grau, especialmente no que se refere à atribuição de valores ao domínio e à obtenção dos valores correspondentes na imagem. Além disso, alguns alunos relataram que já haviam estudado funções quadráticas nas aulas de Física, especificamente no contexto do movimento uniformemente variado.
Embora tenha sido destacado em sala de aula a análise do formato da parábola a partir do coeficiente "a" negativo, observamos que não foi possível constatar uma reflexão correspondente por parte dos alunos. Esse descompasso entre a explicação fornecida e a compreensão dos alunos apresenta um caráter complexo, considerando as diversas variáveis intrínsecas ao processo, como a falta de atenção e o envolvimento dos alunos.
De maneira semelhante, a abordagem gamificada para o estudo dos coeficientes "b" e "c", presente no material de aula, não proporcionou uma visualização efetiva das implicações gráficas ao variá-los, devido à limitação na construção de diferentes tipos de parábolas com o uso exclusivo do jogo. Em contrapartida, ao partir para a representação genérica da função no GeoGebra, a ideia se formou de maneira mais sólida e com uma visualização mais clara.
Essas implicações do uso do GeoGebra convergem com as constatações de Ferreira e Jacobini (2010), que afirmam que o uso de softwares gera muitos benefícios para a aprendizagem dos alunos, pois permite que visualizem problemas reais com diversos níveis de complexidade, além de contribuir para uma maior interação entre eles.
Durante o estudo dos métodos para obter as raízes da função e o vértice da parábola, destacamos pequenas associações com o jogo ao longo da explicação. Ilustramos os zeros ou raízes da função quadrática como o ponto antes de lançar o personagem e o ponto de impacto no alvo, enquanto o ponto de vértice foi exemplificado pela altura máxima alcançada na trajetória do personagem.
Quando retomamos o problema inicial e solicitamos a resolução por meio da função descrita no enunciado, observamos um progresso notável por parte dos alunos na compreensão das implicações gráficas dos coeficientes da função quadrática. Apesar desse avanço, apenas alguns alunos conseguiram chegar ao resultado final. Diante das dificuldades evidenciadas, interviemos, solucionamos o problema, realizamos correções e fornecemos explicações mais detalhadas.
Ao analisar as respostas dos alunos à lista de exercícios, observamos um bom desempenho na resolução das questões que envolviam a análise gráfica. No entanto, ao abordar os conceitos teóricos, identificamos lacunas significativas, especialmente nos procedimentos para determinar as raízes da função e o ponto de vértice. Esse padrão indica a necessidade de uma abordagem mais detalhada na explicação desses conceitos teóricos, com o objetivo de fortalecer a compreensão dos alunos nesses aspectos específicos do entendimento dos conceitos.
Considerações finais
A abordagem gamificada por meio do jogo Angry Birds Friends como recurso didático demonstrou-se, de modo geral, uma estratégia eficaz para despertar o interesse dos alunos. O entusiasmo inicial e a familiaridade dos estudantes com o jogo proporcionaram um ponto de partida atrativo para a exploração dos conceitos matemáticos, favorecendo a compreensão das trajetórias parabólicas associadas ao lançamento de projéteis.
No entanto, observamos algumas limitações do jogo no que diz respeito a exemplificar, em sua totalidade, as representações das parábolas. Ainda assim, conforme discutido ao longo do trabalho, foi possível desenvolver estratégias de edição de imagem para permitir o uso do jogo como uma ponte para a assimilação do conteúdo.
De maneira geral, os resultados da sequência didática confirmam que o uso do jogo como ferramenta gamificada tornou o aprendizado mais envolvente, em consonância com os autores citados neste estudo. Por outro lado, identificamos lacunas na consolidação do entendimento teórico das funções quadráticas, possivelmente influenciadas por múltiplos fatores que podem ser aprofundados em pesquisas futuras no campo da educação matemática.
Referências
ALVES, D. M.; CARNEIRO, R. S.; CARNEIRO, R. S. Gamificação no ensino de Matemática: uma proposta para o uso de jogos digitais nas aulas como motivadores da aprendizagem. Revista Docência e Cibercultura, v. 6, nº 3, p. 146-164, 2022. DOI: 10.12957/redoc.2022.65527. Disponível em: https://www.e-publicacoes.uerj.br/re-doc/article/view/65527. Acesso em: 2 nov. 2023.
ALVES, F. Gamification: como criar experiências de aprendizagem engajadoras. 2ª ed. São Paulo: DVS, 2015.
AMANCIO, D. T.; SANZOVO, D. T. Ensino de Matemática por meio das tecnologias digitais. Revista Educação Pública, v. 20, nº 47, 8 dez. 2020. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/20/47/ensino-de-matematica-por-meio-das-tecnologias-digitais. Acesso em: 2 nov. 2023.
ANDRADE, W. M. Um estudo sobre a aprendizagem das funções quadráticas com a mediação do software GeoGebra. 2017. 170f. Dissertação (Mestrado em Educação) – Universidade Federal do Ceará, Fortaleza, 2017.
BAUMGARTEL, P. O uso de jogos como metodologia de ensino da Matemática. In: ENCONTRO BRASILEIRO DE ESTUDANTES DE PÓS-GRADUAÇÃO DE MATEMÁTICA, 20., 2016, Curitiba. Anais eletrônicos […]. Curitiba, 2016. Disponível em: http://www.ebrapem2016.ufpr.br/wp-content/uploads/2016/04/gd2_priscila_baumgartel.pdf. Acesso em: 17 out. 2023.
FERREIRA, D. H. L.; JACOBINI, O. R. Tecnologia e ambiente de trabalho: uma combinação pedagógica para o ensino de conteúdos matemáticos. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 10. Anais... Salvador, jul. 2010.
FREITAS, S. A.; NETO, A. S. A. A utilização do jogo Angry Birds Space na aprendizagem de conceitos de lançamento de projéteis e de gravidade no Ensino Fundamental: uma proposta de unidade de ensino potencialmente significativa. Revista Brasileira de Ensino de Ciências e Matemática, v. 1, nº 2, p. 214-225, 17 dez. 2018.
LIMA, A. C. O.; NEGRÃO, F. C. O uso de jogos eletrônicos no processo de ensino-aprendizagem de Matemática. Revista Docência e Cibercultura, Rio de Janeiro, v. 6, nº 1, p. 1-16, jan./dez. 2022. DOI: 10.12957/redoc.2022.57587. Disponível em: https://www.e-publicacoes.uerj.br/re-doc/article/view/57587. Acesso em: 13 out. 2023.
MOITA, F. G. S. C. et al. Angry Birds como contexto digital educativo para ensino e aprendizagem de conceitos matemáticos: relato de um projeto. SBC – Proceedings of SBGames, 2013. Disponível em: http://www.sbgames.org/sbgames2013/proceedings/cultura/Culture-17_full.pdf. Acesso em: 13 out. 2023.
NETO, J. F. S. Ensino de Matemática: concepção docente e fazer didático-pedagógico. 2021. 170f. Tese (Doutorado em Educação) – Universidade Federal do Rio Grande do Sul, Porto Alegre, 2021.
SILVA, J. A. B. O uso de jogos no ensino da Matemática. 2022. Monografia (Licenciatura em Pedagogia) – Universidade Federal Rural de Pernambuco, Recife, 2022.
VASCONCELOS, I. C.; ANDRADE, A. N.; NEGRÃO, F. C. Tecendo conhecimentos de multiplicação com o uso da plataforma Khan Academy com alunos do 5º ano do Ensino Fundamental. Reamec - Rede Amazônica de Educação em Ciências e Matemática, v. 8, nº 3, p. 435-448, 2020.
Publicado em 02 de abril de 2025
Como citar este artigo (ABNT)
SOARES, Augusto de Almeida Barros; MÁXIMO, Jamily Leite; FERREIRA, Moizeis Veiga; SILVA, Rayane de França da; SILVA, Tácio Barros da; SILVA NETO, João Ferreira da. Funções quadráticas e o jogo Angry Birds Friends. Revista Educação Pública, Rio de Janeiro, v. 25, nº 12, 2 de abril de 2025. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/25/12/funcoes-quadraticas-e-o-jogo-angry-birds-friends
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

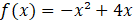 .
. 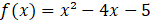 .
. 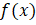 , se houver.
, se houver. 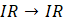 . A lei de formação dessa função é:
. A lei de formação dessa função é: