Construção de conceitos geométricos usando o software GeoGebra: uma proposta para abordagem de semelhança de triângulos
Isabella Trog
Licencianda em Matemática (Unicentro)
Izabel Passos Bonete
Doutora em Ciências Florestais (Unicentro), docente no Departamento de Matemática da Unicentro
As tecnologias digitais e a internet vêm promovendo uma importante transformação no sistema de ensino e na vida das pessoas. A internet possibilita o contato virtual por meio de informações em tempo real com o mundo todo, e os jovens estão imersos nesta realidade há algum tempo. Por esse motivo, somente as metodologias tradicionais usadas pelos professores não têm sido suficientes para motivar e despertar o interesse dos alunos para os estudos.
No ensino da Matemática, as tecnologias digitais podem ser um importante aliado da prática pedagógica do professor e nos diversos momentos de aprendizagem dos estudantes. Não são ferramentas que substituem a presença do professor, mas, nos dias de hoje, são muito importantes para auxiliar o professor no desenvolvimento de uma prática pedagógica diferenciada e motivadora. Devem ser utilizadas como recurso didático que agregue novos conhecimentos aos conteúdos formais, bem como motive seus alunos a se tornarem participativos no processo de ensino-aprendizagem. Entretanto, faz-se necessário que o professor esteja preparado teórico-metodologicamente para trabalhar num ambiente informatizado.
Faz-se necessário que administradores e professores deixem para trás a ideia de que o computador é simplesmente mais um instrumento para ser usado de forma pontual na prática docente e passem a percebê-lo como ferramenta que pode promover desenvolvimento cognitivo e social dos educandos (Maia; Barreto, 2012 apudTorres; Torres, 2016, p. 141).
Atualmente, é possível utilizar recursos como computadores, tablets, smartphones e lousas digitais para facilitar o aprendizado e tornar as aulas mais dinâmicas e interativas. Uma vantagem da tecnologia na área da Educação é a possibilidade de diferenciação do ensino, pois há várias plataformas e diversos softwares de aprendizagem que podem ser usados para focar em uma área específica de conhecimento, podendo identificar as necessidades e dificuldades de cada aluno e trabalhar em cima disso de maneira mais dinâmica. Segundo Torres e Torres (2016), os educadores devem estar atentos ao uso de recursos tecnológicos como meios educacionais, uma vez que devem ser utilizados correta e eficazmente para que se possa ter um ensino-aprendizagem significativo.
A aprendizagem da Matemática se torna, muitas vezes, um grande obstáculo para os alunos do Ensino Básico, visto que muitos possuem dificuldades em compreender a relevância do conteúdo para sua vida fora da escola e muitas vezes têm dificuldades conceituais de aprendizagem, principalmente relacionadas aos conceitos geométricos. Diante dessas circunstâncias, o presente trabalho pretende investigar e discutir o uso do software GeoGebra em uma turma do 9º ano do Ensino Fundamental para a aprendizagem de conceitos da Geometria, especialmente o conteúdo de semelhança de triângulos.
Uso da tecnologia na Educação Matemática
Os professores têm sido desafiados cada vez mais na missão de ensinar seus alunos diante do mundo tecnológico que vivemos. Borba e Penteado (2016) destacam que isso evidencia a necessidade de que os docentes estejam sempre em busca de metodologias que favoreçam a aprendizagem e se mantenham atualizados e capacitados a respeito das novas tendências de ensino, em especial as que utilizam a tecnologia em sala de aula, uma vez que ela está se tornando indispensável para a vida humana.
A tecnologia tem assumido importante papel na área da Educação, oferecendo novas possibilidades e recursos para professores e alunos, uma vez que permite que os estudantes tenham acesso a uma quantidade ilimitada de informações e conteúdo.
O ambiente digital surge como uma nova perspectiva no contexto escolar, abrindo espaço para uma maior interação humana mediada pelos gêneros eletrônicos, através da interdisciplinaridade. A linguagem universal e compartilhada no mundo inteiro transforma o aprendizado do aluno, inserindo-o como sujeito social no contexto educacional e na tecnologia simultaneamente (Dias; Cavalcante, 2016, p. 163).
Diante disso, é possível buscar informações sobre temas específicos e enriquecer o conhecimento em diversas áreas. Tendo foco no ensino da Matemática, a tecnologia pode ser uma grande ferramenta para tornar o aprendizado mais interativo e dinâmico, considerando que um dos principais meios para realizar a aplicação da tecnologia na Educação é por meio de jogos e softwares educativos específicos que permitem a visualização e manipulação de dados, gráficos e equações matemáticas. Oliveira e Cunha (2021) salientam que o uso de um software educativo em sala de aula leva os alunos a aprender o conteúdo de forma dinâmica e pensativa, e não de forma pronta e acabada, tendo assim a oportunidade de aprender de forma participativa e lúdica.
Os softwares educativos são ferramentas de grande utilidade no processo de ensino-aprendizagem, pois podem proporcionar aos estudantes maior compreensão dos conceitos matemáticos e possibilitar a prática dos conceitos já trabalhados em sala de aula, além de propor uma aula mais dinâmica e lúdica. Desse modo, é possível transformar a prática pedagógica tradicional numa prática diferenciada que permite o incentivo da criatividade e o desenvolvimento de habilidades cognitivas dos estudantes.
Uma aula que faz uso desses recursos eficientemente torna-se mais interessante, oferecendo oportunidades para que os alunos inventem e reinventem o conteúdo com seus próprios olhos a partir desse contato com a tecnologia. Segundo Dias e Cavalcante (2016, p. 164),
os professores precisam de habilidades no campo da tecnologia de informação, é necessário repensar a sua prática docente deixando abrir espaço para um novo saber. O papel do professor nesse novo contexto educacional é dar subsídios para que o aluno adquira uma postura autônoma e crítica com total responsabilidade e assim aprenda de forma correta a manejar a tecnologia de informação.
Por essa razão, usar a tecnologia e inseri-la no contexto educacional não é apenas fazer uso de equipamentos ou dispositivos eletrônicos nas aulas. É necessário que o professor, que é o mediador do conhecimento, seja habilidoso para poder apresentar e fazer uso das tecnologias como meio de novas possibilidades de aprendizagem. Para tanto, faz-se necessário o planejamento adequado e a análise de qual ferramenta tecnológica educativa o professor pretende utilizar em suas aulas de Matemática.
Alves (2017) afirma que a escolha de determinado software como ferramenta educacional é de grande importância para o desenvolvimento do trabalho a ser realizado. Vale ressaltar que somente a utilização das tecnologias educativas não significa melhoria no processo de ensino-aprendizagem; é importante lembrar que a tecnologia nunca deve substituir o papel do professor, mas sim complementar e enriquecer o trabalho pedagógico.
Na Educação Matemática, uma área em que os alunos possuem certa defasagem é a Geometria, pois possuem dificuldades de aprendizagem relacionadas aos conceitos geométricos. Dessa forma, os softwares de Geometria dinâmica permitem tornar as aulas mais atrativas, pois a partir deles é possível mostrar as propriedades e construções geométricas que normalmente seriam difíceis de ser mostradas com qualidade somente empregando quadro e giz. O GeoGebra é um dos vários softwares de Geometria dinâmica que o professor e o aluno podem utilizar para dinamizar o ensino, sendo de fácil acesso e fácil compreensão para utilizar.
O software GeoGebra
O GeoGebra é um software livre que dispõe de funções ligadas a Geometria, Álgebra e Cálculo, em uma interface de fácil acesso e uso. Ele foi desenvolvido para auxiliar estudantes e professores de Matemática em atividades de ensino-aprendizagem, possibilitando que seus usuários explorem conceitos e aplicações matemáticas de forma interativa e visual.
O software GeoGebra foi produzido em 2001 por Markus Hohenwanter, pesquisador austríaco da Universidade de Salzburg, na Áustria. O nome GeoGebra surgiu com a junção dos termos Geometria e Álgebra. Mais tarde, o software passou a ser aprimorado e melhorado por um grupo de programadores da Universidade de Florida Atlantic, nos Estados Unidos, sob a coordenação de seu criador e de Judith Hohenwanter.
Por se tratar de um software com a função de auxiliar na aprendizagem, ele possui uma interface de fácil compreensão e boa visualização. A Figura 1 apresenta a interface do software GeoGebra, onde se destacam cinco partes: a barra de menus, a barra de ferramentas, a janela de Álgebra, a janela de visualização e o campo de entrada.
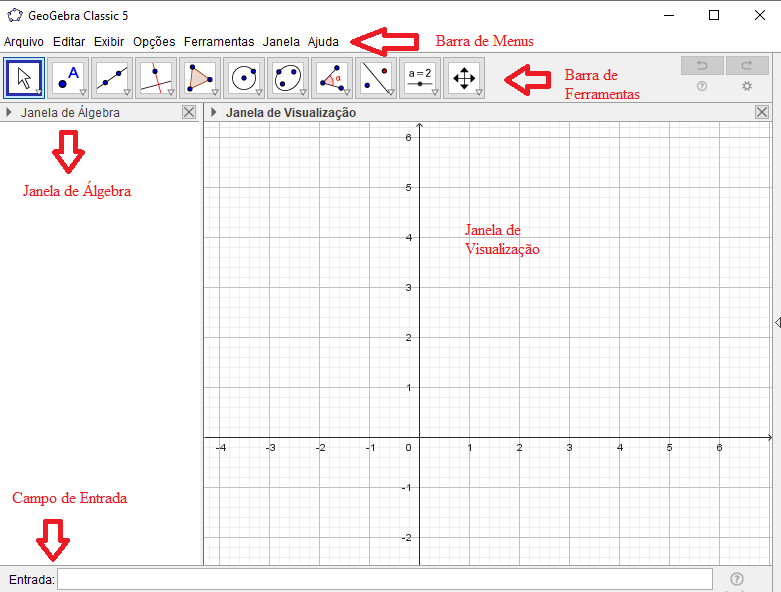
Figura 1: Interface do GeoGebra
A barra de menus é formada por uma barra com certas funções, por meio das quais o estudante pode abrir arquivos, criar arquivos novos, salvar, fechar e configurar ferramentas, entre outros recursos. Essa barra possui as ferramentas que podem ser utilizadas na produção dos objetos de estudo. Cada ícone dessa barra esconde outros ícones que podem ser acessados clicando com o mouse em seu canto inferior direito. A janela de Álgebra apresenta equações das figuras produzidas, coordenadas e valores das medições. A janela de visualização é o espaço destinado à exibição do conteúdo criado pelo usuário, e o campo de entrada é o espaço para o usuário escrever coordenadas de pontos, funções e comandos.
O Quadro 1 apresenta o detalhamento de cada ferramenta, de sua função e de sua representação, que possibilitam uma infinidade de construções de objetos geométricos.
Quadro 1: Ferramentas do GeoGebra
Ferramentas |
Função |
Representação |
Mover |
Move os objetos construídos |
|
Ponto |
Cria um novo ponto |
|
Reta |
A partir de dois pontos marcados traça-se a reta definida por eles |
|
Reta perpendicular |
A partir de uma reta e em um ponto constrói-se uma reta perpendicular à reta considerada, passando pelo referido ponto |
|
Polígono |
Cria um polígono, marcando-se ao menos três pontos e clicando, com o botão esquerdo do mouse, no primeiro ponto novamente |
|
Círculo dados seu centro e um de seus pontos |
Cria um círculo a partir de dois pontos, sendo o centro no primeiro deles e passando pelo outro |
|
Elipse |
Cria uma elipse |
|
Ângulo |
Cria um ângulo |
|
Reflexão em relação a uma reta |
Estabelece a reflexão em relação a uma reta |
|
Controle deslizante |
Permite ajustar o parâmetro em um intervalo de valores predefinidos quando o usuário move o marcador |
|
Mover janela de visualização |
Move janela de visualização |
|
O uso do software GeoGebra como ferramenta para o ensino de Geometria
A Geometria é uma disciplina fundamental no currículo de Matemática. A Base Nacional Comum Curricular (BNCC) (Brasil, 2018) destaca que seu estudo envolve um amplo conjunto de conceitos e procedimentos necessários para resolver problemas do mundo físico e de diferentes áreas do conhecimento, além de ser considerada uma ciência que tem função essencial na formação dos indivíduos, pois é possível encontrá-la em tudo à nossa volta. Segundo Ferreira (1999, p. 983), a Geometria é a
ciência que investiga as formas e as dimensões dos seres matemáticos ou ainda um ramo da Matemática que estuda as formas plana e espacial com as suas propriedades, ou ainda ramo da Matemática que estuda a extensão e as propriedades das figuras (Geometria Plana) e dos sólidos (Geometria no espaço).
No entanto, não deixa de ser uma disciplina escolar, muitas vezes desafiadora para os alunos, independente do ano escolar em que estejam, pois acaba sendo um tanto quanto abstrata e visual. Os alunos possuem certa dificuldade em visualizá-la e fazer a conexão com seu conceito, porém a tecnologia moderna trouxe avanços significativos no ensino dessa disciplina por meio da apresentação de diversas ferramentas tecnológicas com potencial para utilização em sala de aula. Scortegagna (2015) destaca o software GeoGebra por possibilitar novas abordagens de conteúdos antes restritos à sala de aula.
O software em questão emergiu como ferramenta poderosa para tornar o aprendizado da Geometria mais acessível, interativo e envolvente, tornando-o um instrumento mediador no processo de ensino-aprendizagem da Geometria dinâmica, visto que a utilização de ferramentas tecnológicas e pedagógicas atuais no ensino de Matemática contribui efetivamente para criar um ambiente favorável à aprendizagem, melhorando a capacidade de construção do conhecimento matemático por parte do aluno, promovendo assim a autonomia no processo de ensino-aprendizagem.
O GeoGebra possibilita a representação de pontos, vetores, segmentos, retas, circunferências, bem como transportar distâncias, encontrar paralelas e perpendiculares e construir gráficos. Conjecturas são feitas a partir da criação de objetos geométricos e, desse modo, pode-se introduzir os conceitos matemáticos a partir de uma nova visão (Bellemain, 2001).
As dificuldades encontradas pelos alunos em relação à Geometria estão relacionadas à não articulação de métodos didáticos e o conteúdo a ser explorado. Dessa forma, o software GeoGebra torna-se uma metodologia alternativa na Matemática, sendo um recurso facilitador do ensino-aprendizagem da Geometria, buscando construir e fundamentar seus conceitos mediante atividades planejadas.
O GeoGebra é uma ferramenta versátil e essencial para o ensino de Geometria, pois promove uma compreensão mais profunda dos conceitos geométricos, oferecendo recursos para personalizar a aprendizagem de acordo com as necessidades individuais dos alunos. Além de ser um software atuante no ensino, é uma ferramenta que está disponível como aplicativo para desktop e em versões online e para smartphones, tornando-o acessível em uma variedade de dispositivos e sistemas operacionais. Desse modo, o GeoGebra pode ser considerado uma ferramenta versátil e valiosa para a Educação e a exploração da Matemática.
Semelhança de triângulos
Nos anos finais do Ensino Fundamental, o ensino de Geometria deve focar em conteúdos considerados relevantes e que gerem conhecimento para o futuro dos educandos. Um desses conteúdos que permite aos estudantes a compreensão de como figuras podem ser transformadas em diferentes tamanhos, cuja habilidade é fundamental para a compreensão de conceitos mais avançados, como escalas e proporções, utilizadas em atividades de ampliação/redução de figuras geométricas planas é essencial nesse nível de ensino.
Facchini (2021) destaca que, de acordo com a BNCC, nos anos finais do Ensino Fundamental devem ser destacadas, além do enriquecimento e desenvolvimento do aprendizado dos conteúdos dos anos iniciais do Ensino Fundamental, a abordagem e a realização de atividades que avaliam e produzem transformações e ampliações ou reduções de figuras geométricas planas. Esse conhecimento permite aos educandos a identificação dos elementos variantes e invariantes das figuras geométricas planas e possibilitam, assim, o desenvolvimento dos conceitos de congruência e semelhança, que capacitam o aluno a reconhecer as condições necessárias e suficientes para obter triângulos congruentes e semelhantes.
Pela definição de Pesco e Arnaut (2009), dois triângulos são semelhantes se os três ângulos são ordenadamente congruentes e se os lados homólogos são proporcionais, conforme a Figura 2. Dois lados homólogos (homo = mesmo, logos = lugar) são tais que cada um deles está em um dos triângulos e ambos são opostos a ângulos congruentes.
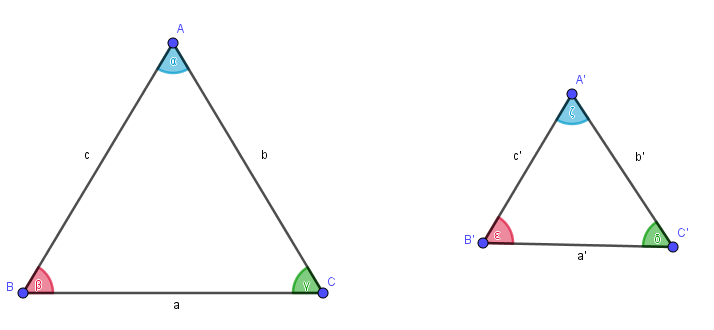
Figura 2: Triângulos semelhantes
A semelhança dos triângulos ABC e A’B’C’ é indicada por:
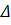 ABC ~
ABC ~
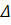 A'B'C'. Entre esses triângulos, pode ser encontrada uma razão de proporcionalidade, ou seja, dividindo a medida de um lado da primeira figura pela medida de um lado correspondente da segunda figura, e o resultado for, por exemplo, um número K, todas as divisões entre medidas de lados da primeira figura por medidas dos lados correspondentes da segunda figura terão K como resultado. Esse número K é denominado razão de proporcionalidade entre os triângulos ABC e A’B’C’.
A'B'C'. Entre esses triângulos, pode ser encontrada uma razão de proporcionalidade, ou seja, dividindo a medida de um lado da primeira figura pela medida de um lado correspondente da segunda figura, e o resultado for, por exemplo, um número K, todas as divisões entre medidas de lados da primeira figura por medidas dos lados correspondentes da segunda figura terão K como resultado. Esse número K é denominado razão de proporcionalidade entre os triângulos ABC e A’B’C’.
Assim, dois triângulos são semelhantes se três ângulos correspondentes são congruentes e três lados correspondentes têm a mesma razão de proporcionalidade, ou seja:
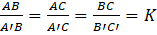
Entretanto, é possível notar a semelhança dos triângulos observando se eles se enquadram em um dos três casos de semelhança de triângulos:
1º Caso: Lado Lado Lado (LLL) - Se dois triângulos possuem três lados proporcionais, então esses dois triângulos são semelhantes. Para esse caso, não se faz necessário verificar se os ângulos e as razões entre os lados correspondentes têm o mesmo resultado;
2º Caso: Lado Ângulo Lado (LAL) - Dois triângulos que possuem dois lados proporcionais e o ângulo entre eles congruente são semelhantes;
3º Caso: Ângulo Ângulo (AA) - Dois triângulos são semelhantes se possuírem dois ângulos correspondentes congruentes.
Procedimentos metodológicos
A presente investigação, caracterizada como relato de experiência, foi desenvolvida por meio de pesquisa bibliográfica e pesquisa de campo. A pesquisa bibliográfica embasou teoricamente o trabalho e proporcionou subsídios para a pesquisa de campo. A pesquisa de campo caracterizou-se como uma investigação e discussão sobre a aplicação de uma proposta de trabalho diferenciada, baseada no uso do software GeoGebra na abordagem da Geometria, especificamente do tema semelhança de triângulos com alunos do 9° ano do Ensino Fundamental de um colégio do município de Irati/PR.
A experiência foi realizada no mês de novembro de 2023, com duração de 2 horas-aula na disciplina de Matemática. Participaram da experiência 26 alunos com idades entre 14 e 15 anos.
As atividades ocorreram em dois momentos: na sala de aula e no Laboratório de Informática do colégio, o qual comportou a turma de alunos, destinando um computador para cada aluno. Primeiramente, em sala de aula, foi realizado um diálogo entre professor e alunos em que foram detectadas as deficiências dos estudantes com relação ao tema proposto e, por meio de uma aula expositiva, abordaram-se os conceitos que os alunos tiveram dificuldades para expor. Ainda em sala de aula, foi abordado o conceito de triângulos semelhantes e realizada uma atividade impressa. Na sequência, os alunos foram familiarizados com aplicativos de Geometria dinâmica por meio de uma breve apresentação do GeoGebra e das ferramentas essenciais para o desenvolvimento da proposta. Para tanto, foi acessado o GeoGebra Online no Educatron da sala de aula.
No Laboratório de Informática, a atividade proposta foi realizada no GeoGebra Online e cada aluno teve a oportunidade de concretizar a sua própria atividade, sendo orientado para a construção da atividade pela professora pesquisadora por meio da projeção do GeoGebra na tela de projeção, utilizando um datashow.
Resultados e discussões
A proposta de construção de conceitos geométricos usando o software GeoGebra na abordagem de semelhança de triângulos foi realizada com estudantes do 9º ano do Ensino Fundamental no período vespertino de um colégio público do município de Irati/PR, localizado na área urbana da cidade e que oferece o Ensino Fundamental II e o Ensino Médio.
A turma em que foi realizada a prática é constituída por 30 alunos, mas no dia da aplicação estavam presentes 26 alunos na faixa etária de 14 a 15 anos. No geral, de acordo com os docentes da escola, a turma é considerada agitada, mas durante a aplicação da prática pedagógica proposta os educandos prestaram atenção e foram participativos. Barbosa e Souza (2015) mencionam que o comportamento agitado e as conversas frequentes em sala de aula caracterizam o modo de ser e pensar dos jovens na atualidade e não têm a intenção de desrespeitar colegas e professores.
A atividade ocorreu no Laboratório de Informática do colégio e na própria sala de aula, sendo realizada em 2 horas-aula de Matemática. O objetivo da proposta era que todas as aulas fossem no Laboratório de Informática; no entanto, por haver somente dois laboratórios para uso de mais de 12 turmas, não foi possível agendar horário para duas aulas no dia em que foi realizado o trabalho. Dessa maneira, a primeira aula ocorreu em sala de aula, sendo utilizada para a apresentação da proposta aos estudantes e para a explicação do trabalho a ser realizado; como os alunos já haviam visto o conteúdo tema do trabalho, a atividade serviu como revisão para os estudantes.
A partir disso, os alunos foram questionados se lembravam e sabiam de alguns conceitos da Geometria, como ângulos e triângulos, e se tinham alguns saberes ou informações sobre o conteúdo de semelhança de triângulos. Nenhum aluno soube conceituar ângulo; entretanto, alguns apresentaram o conceito de triângulo por meio de respostas como: “triângulo é uma figura formada por três ângulos” e “triângulo é uma figura formada por três lados”, mas a grande maioria dos alunos não lembrava algo acerca do conteúdo. Segundo Pivatto (2014), um tema comum nos atuais debates sobre o ensino de Matemática diz respeito à necessidade de conceber os estudantes não somente como ponto de passagem, mas como ponto de partida do processo de ensino, pois eles trazem para a sala de aula um conjunto de explicações sobre determinado assunto, conhecido como conhecimentos prévios, que muitas vezes são pouco elaborados e precisam ser identificados e levados em consideração pelos professores de Matemática, pois diferem dos saberes científicos apresentados pela escola.
Identificados os conhecimentos prévios dos alunos, deu-se início à discussão de semelhança de triângulos, destacando a construção dos conceitos de ângulos e triângulos. Num primeiro momento, foram desenhados no quadro da sala dois triângulos de tamanhos diferentes e nomeados seus vértices e lados. Nesse momento, abordaram-se os conceitos de ângulos e triângulos por meio de uma aula expositiva. Compreendidos os conceitos, solicitou-se aos alunos que verificassem possível semelhança em relação aos triângulos apresentados no quadro, identificando as medidas dos ângulos e lados. Posteriormente, foi abordado o conceito de triângulos semelhantes, e para isso foi entregue uma atividade impressa (Figura 3).
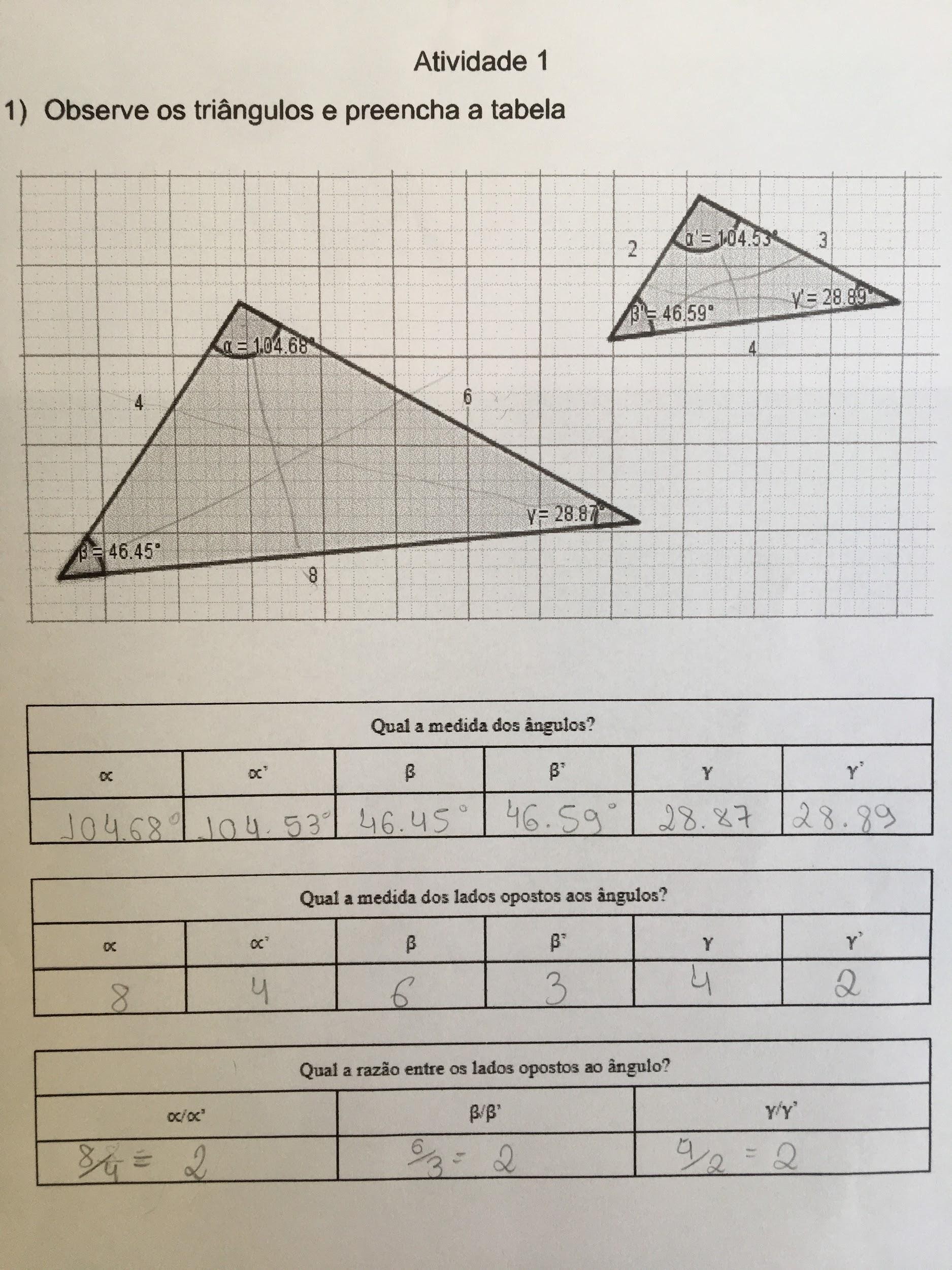
Figura 3: Atividade feita por um aluno
A partir dessa atividade foi possível para os alunos perceber as propriedades entre triângulos semelhantes, conduzindo-os à compreensão das definições e propriedades de semelhança de triângulos.
Os alunos puderam perceber as congruências entre os ângulos correspondentes e a proporcionalidade entre os lados dos triângulos. Foi questionado aos alunos se os triângulos da atividade eram semelhantes. Eles responderam que sim, segundo eles porque “possuíam ângulos iguais”, e quando realizaram a razão entre os lados homólogos obtiveram o mesmo resultado em todos os três lados do triângulo. Nessa atividade a grande maioria dos alunos resolveu facilmente, somente dois alunos precisaram ter auxílio na resolução.
Um segundo momento se deu com a retomada dos casos de semelhança de triângulos. Novamente foi questionado aos alunos se eles recordavam quais eram os três casos de semelhança de triângulos. Nesse momento, um dos estudantes respondeu ao ver as anotações em seu caderno. Ele fez uma leitura das definições anotadas e foi realizada uma retomada de cada caso, realizando exemplos para os alunos relembrarem o conteúdo.
Com isso, os alunos obtiveram uma revisão do conteúdo já trabalhado, podendo relembrar aquilo que já haviam visto em algum momento de seus estudos. Como o próximo passo do trabalho era a construção dos casos de semelhança no software GeoGebra; foi passada brevemente em sala de aula a apresentação do software.
Questionados se já o conheciam e se já haviam utilizado o GeoGebra, nenhum dos alunos manifestou ter conhecimento da plataforma nem sabia como trabalhar com o software. Assim, no fim da primeira aula, foi feita uma breve apresentação do GeoGebra e suas ferramentas. Para isso foi acessado o GeoGebra Online no Educatron da sala de aula, o qual consiste em uma TV de tela plana acoplada a um computador e a uma webcam com conexão à internet via wi-fi. Tendo a visão das ferramentas, foram destacadas aquelas que seriam utilizadas para o propósito da aula e foi ensinado aos alunos como salvar os arquivos que seriam criados.
A segunda aula com a turma foi realizada no Laboratório de Informática do colégio. O laboratório utilizado era constituído por 27 computadores e um notebook para uso do professor, conectado a um datashow. O laboratório comportou os 26 alunos, sendo possível a utilização de um computador por aluno. A atividade foi realizada no GeoGebra Online, visto que os computadores do colégio não possuíam o software instalado; foi sugerido que os estudantes fizessem cadastro/login na ferramenta para que no final da aula fosse possível salvá-la.
Para a atividade ser mais dinâmica e para que os estudantes se habituassem com a plataforma, a construção foi realizada juntamente com os estudantes por meio da projeção do GeoGebra no laboratório, utilizando o datashow. Dessa forma, foi possível que os alunos seguissem os passos recomendados, possibilitando que observassem as ferramentas utilizadas e percebessem o que deveriam criar em cada passo. Cabral e Almeida (2020) também utilizaram o GeoGebra na abordagem de semelhança de triângulos e, para que os alunos realizassem a construção da atividade, eles também deveriam seguir as orientações do professor e, em caso de dúvidas, discutiam-se os conceitos envolvidos até que os alunos compreendessem a construção no software.
Nessa perspectiva, para o desenvolvimento da prática proposta (a construção de um dos casos de semelhança de triângulos no GeoGebra) foi realizada juntamente com os estudantes passo a passo. Ao longo da construção, os alunos tiveram a oportunidade de visualizar alguns conceitos de Geometria, como ponto, semirreta, interseção, ângulo, circunferência e polígono, entre outros. Dessa forma, foi possível relembrar esses conceitos e visualizá-los de uma forma mais dinâmica, além do conteúdo objetivo. Para Oliveira e Cunha (2021), o software educacional disponibiliza aos professores o trabalho com campos conceituais específicos da Matemática, facilitando a aprendizagem de conceitos da área.
Em relação à prática, a cada etapa da construção os alunos eram orientados sobre os passos que deveriam fazer, visto que era a primeira vez que tinham contato com o software, e alguns apresentaram um pouco de dificuldade para utilizá-lo, sendo atendidos e reorientados para que acompanhassem os demais, ora por meio da rediscussão dos conceitos abordados, ora pela retomada dos passos para a construção proposta. No entanto, como esclarecem Cabral e Almeida (2020), esses contratempos não devem constituir obstáculos para o desenvolvimento de atividades nesse sentido, pois tais ações podem propiciar uma abordagem enriquecedora, com potencialidade de transformação e reorientação da própria prática docente.
No decorrer da aula, constatou-se que alguns alunos compreenderam bem o uso do GeoGebra, pois, além de fazer e acompanhar a atividade que estava sendo proposta, também buscavam explorar o software e suas ferramentas, criando figuras utilizando a ferramenta “ponto”. Dessa maneira, foi possível perceber que o software GeoGebra chamou a atenção dos alunos, proporcionando uma aula diferente e mais prática. Morais, Silva e Nascimento (2021) também constataram que a utilização do software GeoGebra possibilitou que os alunos explorassem a construção, o que facilitou a compreensão pela visualização e permitiu a manipulação das construções, experiência esta que não seria possível apenas com o uso de lápis e papel.
A grande maioria dos alunos acompanhou bem os passos e poucos tiveram que ter um maior auxílio para entender como funcionava a ferramenta. Para Ferreira et al. (2023), a integração dessa ferramenta em sala de aula demonstra ser uma forma eficiente de abordagem e muito satisfatória no processo de aprendizado matemático.
No final da construção, foi questionado aos alunos qual dos três casos vistos na aula anterior tratava a construção realizada no GeoGebra. Os alunos não tiveram dúvidas ao responder que se tratava do 1º caso, ou seja, o caso Lado Lado Lado. Pelo resultado obtido com o uso da ferramenta, foi possível notar que os alunos tiveram facilidade em visualizar a construção com o software GeoGebra, o que era um dos objetivos da proposta.
A Figura 4 exemplifica a construção realizada pelos alunos no software.
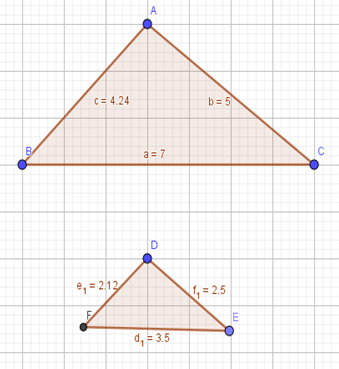
Figura 4: Exemplificação do caso LLL no software
Foi utilizada 1 h/a somente para construção de um dos casos de semelhança, visto que era o primeiro contato dos estudantes com a plataforma e que foi preciso repassar alguns passos para alguns alunos que apresentaram mais dificuldade. Posteriormente, buscou-se agendar mais alguns horários no Laboratório de Informática com o intuito de construir os outros casos; no entanto, não havia horários disponíveis e os alunos estavam em provas finais de semestre. Logo, a aplicação teve seu enfoque somente em um dos casos de semelhança de triângulos.
Com isso, constatou-se que os alunos demonstraram mais interesse pelo conteúdo ao utilizar uma ferramenta diferente daquela com que estão habituados. Para Borba e Penteado (2016), o uso da tecnologia no ensino contribui para um ambiente de aprendizagem mais agradável, pois facilita a aprendizagem e permite ao aluno outras formas para compreender o assunto proposto.
Essa experiência possibilitou também o uso de uma metodologia diversificada, empregando a tecnologia a favor do ensino. Morais, Silva e Nascimento (2021) também constataram que o ensino do conteúdo semelhança de triângulos envolvendo o software GeoGebra permite uma atividade diferenciada da habitual sala de aula e quadro, proporcionando uma aula mais divertida e prazerosa, além de permitir que o aluno crie uma conjectura inicial sobre semelhança de triângulos.
O GeoGebra veio como uma nova ferramenta interativa para os alunos, tornando o aprendizado da Geometria mais acessível e envolvente, sendo um instrumento de auxílio para um conteúdo que os alunos já haviam visto, contribuindo efetivamente para um ambiente de aprendizagem favorável e instigante.
Considerações finais
Para que a Matemática possa ser mais bem entendida pelo estudante, faz-se necessária a busca do professor por novas formas de ensinar e aprender. O presente trabalho teve por finalidade investigar e discutir a utilização do software GeoGebra para despertar maior interesse dos estudantes e contribuir em sua capacidade de relacionar o abstrato ao concreto. Procurou-se propor atividades que buscassem explorar a produção do pensamento geométrico através da visualização e manipulação das figuras com o intuito de criar no aluno uma atitude de observação e investigação das propriedades das figuras.
Logo, o presente trabalho permitiu aos estudantes apreciar um ensino diversificado e mais dinâmico, proporcionando maior incentivo e motivação. O conhecimento adquirido pelos alunos, as atividades realizadas e a construção dos conceitos matemáticos foram o diferencial na prática realizada, sendo fundamentais para atingir os objetivos propostos.
Referências
ALVES, W. F. M. Uso do GeoGebra no ensino de Geometria Plana no Ensino Básico. 2017. 76f. Dissertação (Mestrado Profissional em Matemática) - Unidade Acadêmica Especial de Ciências Exatas e Tecnológicas, Universidade Federal de Goiás, Jataí, 2017.
BARBOSA, E. T.; SOUZA, V. L. T. Sentidos do respeito para alunos: uma análise na perspectiva da Psicologia Histórico-Cultural. Psic. Ciência e Profissão, v. 35(2), p. 255-270, 2015.
BELLEMAIN, F. Geometria dinâmica: diferentes implementações, papel da manipulação direta e usos na aprendizagem. In: INTERNATIONAL CONFERENCE ON GRAPHICS ENGINEERING FOR ARTS AND DESIGN. São Paulo: USP, 2001. p. 1.314-1.329.
BRASIL Ministério da Educação. Base Nacional Comum Curricular. Brasília: MEC, 2018.
BORBA, M. C.; PENTEADO, M. G. Informática e Educação Matemática. 5ª ed. Belo Horizonte: Autêntica, 2016.
CABRAL, A. F.; ALMEIDA, T. C. S. de. Semelhança de triângulos e GeoGebra: uma alternativa de ensino por meio de representações. Revista Sergipana de Matemática e Educação Matemática, nº 1, p. 358–375, 2020.
DIAS, G. A.; CAVALCANTI, R. de. A. As tecnologias da informação e suas implicações para a educação escolar: uma conexão em sala de aula. Revista de Pesquisa Interdisciplinar, v. 1, ed. especial, p. 160-167, 2016. Disponível em: https://cfp.revistas.ufcg.edu.br/cfp/index.php/pesquisainterdisciplinar/article/view/80/59. Acesso em: 14 mar. 2023.
FACCHINI, C. Uma proposta de atividades de semelhança de triângulos para o Ensino Fundamental. 2021. 78f. Dissertação (Mestrado Profissional em Matemática) - Programa de Pós-Graduação Profmat, Universidade Estadual Paulista, São José do Rio Preto, 2021.
FERREIRA, A. Novo Dicionário Aurélio da Língua Portuguesa. 2ª ed. Rio de Janeiro: Nova Fronteira, 1999.
FERREIRA, G. J.; ARAÚJO, M. L.; LOPES, R. T.; VIANA, F. N. de M.; BRITO, J. C. S. A utilização do software GeoGebra para o ensino da Geometria Plana no Ensino Fundamental: algumas demonstrações do teorema de Pitágoras. In: CONGRESSO NACIONAL DE EDUCAÇÃO, 9., 2023, João Pessoa. Anais… Campina Grande: Realize, 2023. Disponível em: https://www.editorarealize.com.br/artigo/visualizar/99218. Acesso em: 05 fev. 2024.
MORAIS, Á. R. S.; SILVA, L. B.; NASCIMENTO, D. L. O ensino de Matemática durante a pandemia: proposta de atividade sobre semelhança de triângulos com uso do software GeoGebra - Geometria. Revista Educação Pública, Rio de Janeiro, v. 21, nº 26, 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/26/o-ensino-de-matematica-durante-a-pandemia-proposta-de-atividade-sobre-semelhanca-de-triangulos-com-uso-do-isoftwarei-geogebra-geometria. Acesso em: 27 jan. 2024.
OLIVEIRA, E. R. de; CUNHA, D. da S. O uso da tecnologia no ensino da Matemática: contribuições do software GeoGebra no ensino da função do 1º grau. Revista Educação Pública, Rio de Janeiro, v. 21, nº 36, 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/36/o-uso-da-tecnologia-no-ensino-da-matematica-contribuicoes-do-isoftwarei-geogebra-no-ensino-da-funcao-do-1-grau. Acesso em: 06 fev. 2024.
PESCO, D. U.; ARNAUT, R. G. T. Geometria Básica. 4ª ed. Rio de Janeiro: Fundação Cecierj, 2009. v. 1.
PIVATTO, W. B. Os conhecimentos prévios dos estudantes como ponto referencial para o planejamento de aulas de Matemática: análise de uma atividade para o estudo de Geometria Esférica. Revemat, Florianópolis, v. 9, nº 1, p. 43-57, 2014.
SCORTEGAGNA, L. Informática na Educação. Juiz de Fora: UFJF, 2015.
TORRES, D. L. L.; TORRES, V. L. J. Análise da inserção das tecnologias digitais como contribuição no processo de ensino-aprendizagem do ambiente escolar visando novas práticas pedagógicas. Revista de Pesquisa Interdisciplinar, v. 1, ed. especial, p. 138-144, 2016. Disponível em: https://cfp.revistas.ufcg.edu.br/cfp/index.php/pesquisainterdisciplinar/article/view/77/56. Acesso em: 26 fev. 2023.
Publicado em 09 de abril de 2025
Como citar este artigo (ABNT)
TROG, Isabella; BONETE, Izabel Passos. Construção de conceitos geométricos usando o software GeoGebra: uma proposta para abordagem de semelhança de triângulos. Revista Educação Pública, Rio de Janeiro, v. 25, nº 13, 9 de abril de 2025. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/25/13/construcao-de-conceitos-geometricos-usando-o-software-geogebra-uma-proposta-para-abordagem-de-semelhanca-de-triangulos
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.