Um estudo de caso nos anos finais do Ensino Fundamental: a aplicação de jogo no ensino de números inteiros

A Matemática desempenha papel fundamental na história da humanidade, adaptando-se ao longo dos anos e permanecendo relevante na sociedade contemporânea (Saviani, 2023). No entanto, muitos alunos enfrentam desafios e dificuldades para compreender certos conceitos, especialmente aqueles relacionados a números inteiros e suas operações, que são fundamentais na Matemática básica.

Os números inteiros, resultado da expansão dos números naturais, surgiram para resolver situações cotidianas que os números naturais não podiam abranger (Souza, 2019). Enquanto os números naturais eram adequados para contagem de objetos e representação de quantidades positivas, mostraram-se insuficientes para lidar com conceitos como dívidas, temperaturas abaixo de zero ou posições em relação a um ponto de referência. A necessidade de números negativos, opostos aos naturais, emergiu para solucionar esses e outros desafios.

Essa extensão do sistema numérico permitiu uma representação mais abrangente e precisa das quantidades e dos fenômenos encontrados no cotidiano, contribuindo para avanços substanciais em diversos campos do conhecimento matemático e suas aplicações práticas (Silva, 2020). Para compreender a importância dos números inteiros, é fundamental definir o conceito subjacente a eles. Os números inteiros incluem tanto os positivos quanto os negativos, juntamente com o zero, formando um conjunto infinito na reta numérica. Essa característica de oposto e a presença de um elemento neutro são fundamentais para o desenvolvimento de várias operações matemáticas e para a resolução de problemas práticos em diversas áreas, como Física, Economia e Engenharia, entre outros (Zanardini, 2017).

Os números inteiros desempenham papel relevante em uma variedade de contextos matemáticos e práticos (Rodrigues, 2009), como temperaturas, altitudes, saldo bancário, pontuações e coordenadas geográficas, desde cálculos simples até problemas complexos de álgebra e teoria dos números. Portanto, compreender profundamente os números inteiros não apenas fortalece as habilidades matemáticas dos alunos como também os capacita a enfrentar desafios do mundo real que exigem pensamento crítico e resolução de problemas.

Desse modo, o estudo dos números inteiros é de suma importância para o desenvolvimento do raciocínio matemático dos alunos nos anos finais do Ensino Fundamental (Seabra, 2023). Esse conjunto numérico é a base para inúmeras operações e situações-problema, influenciando diretamente o aprimoramento do raciocínio lógico e a capacidade de resolver problemas.

Nesse contexto, este trabalho propõe uma análise aprofundada sobre a aprendizagem e o domínio dos números inteiros por parte dos alunos. Muitos deles encontram dificuldades em estudar tal conteúdo devido à abstração e à dependência de métodos tradicionais de ensino, resultando em uma lacuna no avanço dessas competências.

Assim, este estudo tem como pergunta problema: como identificar as lacunas de aprendizagem dos alunos dos anos finais do EF no município de Cascavel com ensino dos números inteiros? Observa-se que os desafios enfrentados e as estratégias pedagógicas para promover o entendimento pleno desse conteúdo é importante na formação matemática dos estudantes.

O objetivo deste estudo é analisar as lacunas de aprendizagem com alunos do sétimo ano do Ensino Fundamental (EF) no ensino dos números inteiros, utilizando o Intege Bank como estratégia de ensino em uma escola de Cascavel/CE.

O estudo visa avaliar o entendimento dos alunos em relação aos conceitos essenciais dos números inteiros, identificando suas dificuldades e lacunas de aprendizado. Também busca-se ver como atividades práticas e recreativas impactam na compreensão dos números inteiros pelos alunos, procurando identificar abordagens pedagógicas mais eficazes (Souza; Ribeiro; Silva, 2024). Este trabalho pretende contribuir para um melhor entendimento do processo de ensino-aprendizagem, fornecendo feedbacks valiosos para educadores e pesquisadores interessados em aprimorar o ensino de Matemática nessa fase escolar.

A estrutura deste trabalho está organizada da seguinte maneira: os fundamentos teóricos relacionados aos números inteiros, ensino de Matemática nos anos finais do EF com os jogos no ensino de Matemática; em seguida, o percurso metodológico utilizado, incluindo detalhes sobre a abordagem adotada, o método de estudo de caso e os procedimentos de coleta e análise de dados. Posteriormente, serão apresentados e discutidos os resultados obtidos, com ênfase nas principais descobertas e padrões identificados durante o processo investigativo.

Finalmente, na seção de considerações finais, serão oferecidas reflexões sobre os resultados, suas implicações para a prática educacional e sugestões para pesquisas futuras. Este trabalho é estruturado na proporção de uma compreensão completa e aprofundada do tema abordado, contribuindo para o avanço do conhecimento no campo da Educação Matemática nos anos finais do Ensino Fundamental.

Fundamentação teórica

Contextualização histórica dos números inteiros

A incorporação do conceito de números inteiros ao corpo teórico da Matemática foi um processo longo e gradual. Nesta subseção, será realizada uma análise breve das primeiras aparições dos números inteiros e como diversas civilizações começaram a reconhecer a importância desse conjunto. Hoje em dia, sua presença é onipresente em nosso cotidiano, refletindo sua ampla disseminação e utilidade.

Durante muito tempo, a humanidade enfrentou desafios para conceber os números negativos (-1, -2, -3, -4 etc.), os quais utilizamos diariamente para expressar, por exemplo, temperaturas abaixo de zero ou saldos devedores em contas bancárias (Ifrah, 1998). A aceitação e a compreensão dos números negativos representam um avanço importante no desenvolvimento do pensamento matemático, facilitado pela descoberta do conceito de zero e pelos progressos na álgebra moderna (Ifrah, 1998).

Esse autor destaca que a mudança na compreensão dos números negativos sublinha o desenvolvimento do pensamento matemático ao longo da história. O que antes parecia confuso e inaceitável agora é amplamente utilizado para representar uma variedade de situações. A aceitação dos números negativos como parte integrante da Matemática contemporânea reflete o avanço do conhecimento e uma mudança fundamental na percepção da disciplina.

Encontrar uma definição abrangente e exclusiva para os números inteiros pode ser desafiador, pois muitos recursos tendem a focar diretamente em sua aplicação em vez de definir seu significado intrínseco. Segundo a visão de Millies e Coelho (2006), os números inteiros representam uma extensão dos números naturais, enriquecidos com atributos distintos, incluindo a garantia de que cada elemento nesse conjunto numérico possui um antecessor.

De acordo com Medeiros e Medeiros (1992), a origem exata dos números negativos ainda é envolta em mistério. Contudo, registros indicam que uma das primeiras menções foi encontrada em um antigo texto chinês denominado Nove capítulos sobre a arte matemática, datado de aproximadamente 200 a.C. Os autores também mencionam que há incertezas quanto à aceitação real dos números negativos pela comunidade chinesa naquela época.

Assim, o conjunto dos números inteiros pode ser compreendido como uma extensão dos números naturais, porém com suas próprias complexidades e incertezas. Enquanto os números naturais são utilizados para contar objetos de forma natural, os inteiros ampliam esse conceito ao incluir números negativos. No entanto, mesmo essa definição aparentemente simples revela-se intricada quando examinada detalhadamente. A natureza abstrata dos inteiros suscita questões sobre sua representação e aplicação em diversos contextos matemáticos e práticos. Portanto, embora se possa entender os inteiros como uma extensão dos números naturais, sua definição completa e suas implicações podem ser menos evidentes do que inicialmente presumido.

Segundo Campos (2001), os números negativos emergiram da necessidade inicial de representar restos e diferenças, mas sua aceitação definitiva ocorreu quando passaram a ser utilizados de maneira mais sistemática no cálculo e na resolução de problemas algébricos e de equações.

Levando em consideração registros chineses, Soares (2008) também apresenta um relato intrigante sobre o estudo dos números inteiros. No século III, os antigos chineses utilizavam barras vermelhas e pretas como símbolos de valores, distinguindo entre positivos e negativos e empregando estes últimos para representar subtrações.

Millies e Coelho (2006) exploram no seu trabalho o histórico do surgimento do estudo dos números negativos. Segundo os autores, o interesse inicial pelos números negativos surgiu a partir de um texto indiano atribuído a Brahmagupta no qual eram concebidos como representações de dívidas. Posteriormente, os números negativos foram gradualmente reconhecidos devido às diversas interpretações que surgiram, embora tenham enfrentado preconceitos e resistência antes de serem plenamente aceitos como um conjunto legítimo para estudo.

A incorporação dos números negativos no sistema matemático representou um marco fundamental na evolução da Álgebra e das equações. A aceitação desses números permitiu a compreensão mais ampla e precisa de uma variedade de fenômenos matemáticos e físicos. Inicialmente associados à representação de dívidas, os números inteiros negativos desencadearam uma revolução conceitual, fornecendo uma linguagem matemática rica para descrever uma ampla gama de situações.

Sua aceitação não apenas ampliou o alcance das operações matemáticas como também estabeleceu as bases para o desenvolvimento de conceitos mais complexos, como números complexos e cálculos vetoriais, fundamentais em muitos campos da ciência moderna.

Na Grécia Antiga, a concepção de números negativos era rejeitada (Sá; Anjos, 2011). Medeiros e Medeiros (1992) destacam que, na obra de Diofantino, um proeminente matemático grego, os números negativos eram abordados de forma implícita. O surgimento dos estudos algébricos inevitavelmente confrontava o desafio dos números negativos, como evidenciado pela equação ax + b = 0, onde a e b são positivos, resultando em uma raiz negativa. No entanto, tais raízes eram consideradas falsas pelos gregos. Essa relutância em aceitar os números inteiros sugere que, para os gregos, era mais conveniente discutir raízes falsas do que analisar a natureza dos números negativos (Medeiros; Medeiros, 1992).

Na Europa, conforme Sá e Anjos (2011), também houve uma forte resistência em relação aos números negativos, e, apesar dos desenvolvimentos de Brahmagupta, muitos matemáticos europeus nos séculos XVI e XVII não apreciavam os números negativos e, se esses números apareciam em seus cálculos, consideravam-nos falsos ou impossíveis (Sá; Anjos, 2011).

Apesar da oposição na civilização europeia, alguns matemáticos europeus contribuíram significativamente para os estudos dos números negativos, como Stevin, Cardano e Viéte. Simon Stevin, um matemático belga, foi pioneiro ao considerar os números negativos como raízes e coeficientes em equações. Girolamo Cardano, matemático italiano, categorizou os números em "falsos" e "verdadeiros", incluindo os "falsos" como raízes complexas e negativos, enquanto os "verdadeiros" compreendiam números naturais, frações positivas e alguns racionais. François Viéte, matemático francês, é creditado pela introdução dos símbolos "+", "-" e "=", embora originalmente fossem usados apenas para subtração entre números positivos (Sá; Anjos, 2011).

Portanto, a rejeição inicial aos números negativos reflete um período na história da Matemática em que conceitos considerados abstratos e contraintuitivos enfrentaram grande resistência. Apesar das contribuições importantes de alguns matemáticos para o estudo dos números inteiros, a aceitação dos números negativos foi uma batalha árdua e demorada.

A negação desses números foi alimentada pela dificuldade de conceber quantidades que representassem dívidas em um contexto matemático. Somente com o tempo e o avanço do pensamento matemático os números negativos foram finalmente integrados ao sistema numérico, revelando-se ferramentas essenciais para a resolução de uma ampla variedade de problemas matemáticos.

Com esse breve histórico sobre os números inteiros, fica evidente a dificuldade enfrentada por renomados matemáticos em todo o mundo durante muito tempo para aceitar e compreender os números negativos. Segundo Soares (2008), essa aceitação teve início por volta de 1650, quando os números negativos começaram a encontrar aplicações práticas, facilitando assim sua compreensão.

Jogos no ensino de Matemática

Conforme destacado por Vygotsky (2002), o jogo desempenha papel fundamental no desenvolvimento do indivíduo, não sendo apenas uma atividade inata, mas sim uma prática influenciada pelas interações sociais. Assim, o jogo carrega consigo significados sociais que variam conforme o tempo e a cultura em que se insere.

Para Kishimoto (2017), as crianças são motivadas a utilizar sua inteligência quando estão engajadas em jogos. Esse desejo as impulsiona a superar obstáculos tanto cognitivos quanto emocionais, tornando-as mais ativas mentalmente.

A pesquisa de Grando (2000) evidencia que o uso de jogos como recurso didático no ensino da Matemática, combinado com atividades em grupo que permitem a intervenção do professor em momentos diversos, revelou-se importante no processo de ensino-aprendizagem da disciplina.

A utilização de jogos no ensino de Matemática demonstra ser uma metodologia dinâmica e envolvente, proporcionando aos alunos uma abordagem lúdica e interativa para compreender conceitos frequentemente abstratos e desafiadores. Especificamente no contexto dos números inteiros, essa abordagem pode ser particularmente benéfica ao permitir a visualização e a manipulação concreta dos números, facilitando a compreensão das operações e propriedades matemáticas.

Os jogos educativos não apenas oferecem diversão; também promovem o desenvolvimento de habilidades cognitivas como o raciocínio lógico, a resolução de problemas e o pensamento crítico (Savi; Ulbricht, 2008). Além disso, incentivam a colaboração e uma competição saudável entre os alunos, o que pode aumentar o engajamento e a motivação para aprender.

Os professores podem complementar o uso de jogos com atividades de reflexão e discussão, ajudando os alunos a conectar a experiência lúdica com os conceitos matemáticos estudados. Essa prática consolida o aprendizado e desenvolve habilidades metacognitivas essenciais para o sucesso acadêmico dos alunos.

Portanto, o uso de jogos no ensino de números inteiros representa uma estratégia inovadora para enfrentar os desafios tradicionais no aprendizado da disciplina. Ao criar um ambiente de aprendizagem atraente, os jogos contribuem para o desenvolvimento das competências matemáticas dos alunos e para o fortalecimento contínuo do interesse pela Matemática.

Metodologia

A pesquisa em questão é caracterizada por um estudo de natureza descritiva e exploratória, utilizando abordagens qualitativas e quantitativas; é implementada com a aplicação de questionários. Conforme delineado por Cunha (1982), o questionário consiste em uma série de perguntas elaboradas pelo pesquisador com base nos objetivos da investigação, oferecendo diversas vantagens, como maior liberdade de expressão e tempo para o respondente, além da redução potencial de vieses nas respostas obtidas, uma vez que o próprio entrevistado preenche o questionário sem influência externa.

Segundo Prodanov e Freitas (2013), a pesquisa descritiva visa registrar de forma imparcial e detalhada os fatos observados, sem interferência do pesquisador. Seu objetivo principal é descrever minuciosamente as características de determinada população ou fenômeno e estabelecer relações entre variáveis. Para tanto, são empregadas técnicas padronizadas de coleta de dados, como questionários e observação sistemática. Tipicamente, a pesquisa descritiva assume a forma de estudos de caso ou levantamentos, buscando proporcionar uma visão ampla e precisa do objeto de estudo.

Em adição, conforme Prodanov e Freitas (2013), a pesquisa exploratória representa uma fase inicial da investigação cujo propósito primordial é proporcionar uma compreensão mais ampla do tema estudado, auxiliando na definição e delimitação do objeto de pesquisa. Essa modalidade de pesquisa visa guiar a seleção e o enfoque dos conteúdos, além de facilitar a formulação de hipóteses ou mesmo a descoberta de novas abordagens sobre o assunto. Geralmente, a pesquisa exploratória assume diferentes formas, como revisões bibliográficas e estudos de caso, visando explorar e compreender mais profundamente o fenômeno investigado.

Os estudos que envolvem pesquisa descritiva frequentemente adotam uma abordagem integradora de métodos qualitativos e quantitativos, uma vez que essas abordagens não são mutuamente exclusivas, mas sim complementares, formando duas vertentes interligadas de investigação (Gamboa, 1995). Enquanto os métodos quantitativos permitem a mensuração e análise estatística dos dados coletados, os métodos qualitativos oferecem uma compreensão mais detalhada e profunda dos fenômenos estudados, possibilitando a identificação de percepções e contextos que não seriam capturados pela abordagem quantitativa apenas. Essa combinação metodológica viabiliza uma análise abrangente e detalhada dos aspectos descritos e das relações estabelecidas na pesquisa descritiva.

Para a condução deste estudo, optou-se pela abordagem de estudo de caso. Esse método, amplamente utilizado na pesquisa científica, permite uma análise minuciosa e profunda de fenômenos complexos em seu contexto natural. Por meio do estudo de caso, buscar-se-á compreender em profundidade os diferentes aspectos relacionados ao tema da pesquisa.

Conforme Prodanov e Freitas (2013), o estudo de caso envolve a coleta e a análise de informações sobre um indivíduo específico, uma família, um grupo ou uma comunidade, com o objetivo de investigar vários aspectos de suas vidas, de acordo com o tema da pesquisa.

Dessa forma, o estudo de caso é um tipo de pesquisa reconhecido, que pode incorporar abordagens tanto qualitativas quanto quantitativas, dependendo dos objetivos da investigação. Seu propósito é examinar detalhadamente uma única unidade de análise, que pode ser um indivíduo, um grupo de pessoas ou uma comunidade, garantindo que o estudo seja conduzido em seu contexto natural para assegurar a validade dos resultados (Prodanov; Freitas, 2013).

Participantes

O estudo foi conduzido em duas turmas do 7° ano do Ensino Fundamental em uma escola municipal de Cascavel/CE, envolvendo um total de 79 alunos.

Instrumentos

Para isso, foram administrados questionários de pré-teste e pós-teste no Google Formulário (Forms), com o intuito de analisar a progressão do aprendizado dos alunos antes e depois da intervenção com o jogo.

Quadro 1: Questões aplicadas aos alunos

Procedimentos

A coleta de dados foi realizada de maneira sistemática no LibreOffice Calc, permitindo a comparação dos resultados e a avaliação do impacto do jogo no processo de aprendizagem dos alunos. Inicialmente, para entender o conhecimento prévio dos alunos sobre números inteiros, especialmente os negativos, aplicamos um questionário de cinco questões na primeira aula, no momento em que o conteúdo foi introduzido. Esse questionário, com três perguntas objetivas e duas subjetivas, buscou avaliar o que os estudantes já sabiam sobre conceitos, propriedades e aplicações de números inteiros. As atividades propostas os desafiaram a resolver problemas envolvendo identificação, cálculo e compreensão de números positivos e negativos, com foco em operações de adição e subtração.

Figura 1: Primeiro contato com o Intege Bank

Fonte: Acervo dos autores (2024).

A aplicação foi individual e durou 50 minutos. Durante esse processo, notamos que o conhecimento prévio dos alunos sobre o tema era, em grande parte, limitado; poucos conseguiram responder às questões com êxito. A novidade do conteúdo e o primeiro contato com o conjunto dos números inteiros, até então desconhecido para a maioria, claramente impactaram os estudantes.

Análise de dados

Após a etapa de pré-teste, dedicamo-nos à criação de uma ferramenta lúdica e engajadora para facilitar a compreensão do conteúdo. Com o objetivo de aproximar a Matemática do cotidiano dos alunos e, ao mesmo tempo, tornar o aprendizado atrativo, desenvolvemos o Intege Bank. Esse jogo de cartas foi concebido para fortalecer o entendimento da adição algébrica e da comparação de números inteiros.

O Intege Bank é composto por 30 cartas: 6 são utilizadas para iniciar o jogo, e as 24 restantes simulam movimentações bancárias cotidianas, como transações via PIX, pagamentos de boletos, compras em supermercados e despesas com energia e internet. Os alunos são organizados em grupos de seis a sete integrantes, dependendo do número total de alunos da turma. Cada grupo recebe uma carta inicial que identifica o jogo e uma quantia inicial igual para todos. A partir daí, os grupos utilizam essa quantia para realizar as movimentações indicadas nas cartas sorteadas. Conforme o jogo avança, o saldo bancário dos grupos aumenta ou diminui, de acordo com as cartas retiradas. Ao final, o grupo vencedor é aquele com o maior saldo positivo ou, em caso de saldos negativos, aquele com a menor dívida.

No dia da aplicação do jogo, os alunos foram acolhidos e as regras foram minuciosamente explicadas. Durante a atividade, monitoramos o andamento do jogo para assegurar o envolvimento e a plena compreensão das dinâmicas propostas. Ficou evidente o entusiasmo e o grande interesse dos alunos, que se mostraram visivelmente envolvidos com a proposta. A aplicação do jogo ocorreu de forma tranquila, refletindo positivamente a dinâmica do Intege Bank como ferramenta educacional dinâmica.

Posteriormente à aplicação do jogo, realizamos um pós-teste para analisar a efetividade do método. Para tal, empregamos o mesmo questionário utilizado no pré-teste, o que possibilitou uma comparação direta dos resultados e a verificação de possíveis avanços na compreensão dos alunos. O pós-teste foi conduzido no mesmo período de 50 minutos, garantindo condições idênticas às do pré-teste para uma análise comparativa precisa.

Resultados e discussão

A aplicação dos métodos mencionados permitiu a obtenção de dados que revelam tendências e padrões relevantes do objeto de estudo. Os resultados detalhados dos questionários de pré-teste e pós-teste fornecem uma análise dos dados coletados, destacando os principais achados e suas implicações para a pesquisa. O pré-teste foi projetado para avaliar o conhecimento prévio e as habilidades dos participantes em relação aos números inteiros, servindo como base para comparações com os resultados após a intervenção.

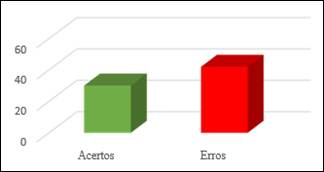
Gráfico 1: Primeira pergunta do pré-teste

Ao analisar o Gráfico 1, fica evidente que a primeira questão apresentou um contexto do cotidiano dos alunos entre lucro e prejuízo. Entre os 79 alunos avaliados, somente 33 responderam corretamente, enquanto 46 cometeram erros. Esses resultados indicam que mais da metade dos alunos encontrou dificuldade ao classificar os valores, revelando uma compreensão insuficiente dos conceitos abordados. O elevado índice de erros ressalta a necessidade de reforçar o entendimento sobre a diferença entre lucro e prejuízo.

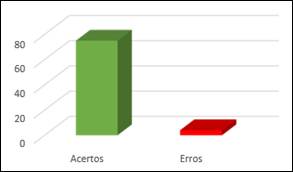
Gráfico 2: Primeira pergunta do pós-teste

Ao analisar os resultados do Gráfico 2, observamos uma notável melhoria no pós-teste em comparação com o pré-teste. No pré-teste, menos de metade dos 79 alunos conseguiu responder corretamente à primeira questão, que envolvia a classificação dos itens como positivos ou negativos. Muitos alunos enfrentaram dificuldades específicas ao atribuir corretamente o lucro como positivo e o prejuízo como negativo (Medeiros; Medeiros, 1992).

Entretanto, após a utilização do Intege Bank, os resultados do pós-teste demonstraram avanço significativo, com 75 alunos respondendo corretamente à mesma questão.

A segunda questão do teste abordava a compreensão sobre saldo bancário e a identificação de situações de déficit. Essa questão avalia a habilidade dos alunos em realizar operações básicas de subtração e compreender os conceitos de saldo positivo e negativo, fundamentais para a gestão financeira pessoal.

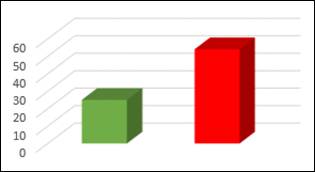
Gráfico 3: Segunda pergunta do pré-teste

No pré-teste (Gráfico 3), a análise da segunda questão revela uma dificuldade significativa dos alunos em lidar com problemas bancários que envolvem saldos negativos. Apenas 25 dos participantes responderam corretamente, enquanto 54 cometeram erros. Esses resultados destacam que a maioria dos alunos encontrou dificuldades em compreender no jogo que uma retirada maior que o saldo disponível resultaria em saldo negativo. A alta taxa de erros aponta para uma lacuna importante no entendimento de conceitos financeiros básicos, indicando a necessidade de reforço e maior foco nesse tipo de conteúdo.

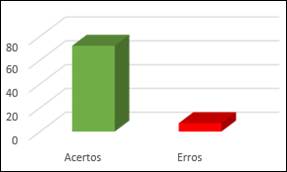
Gráfico 4: Segunda pergunta do pós-teste

No pós-teste da segunda questão, houve melhora: 72 alunos acertaram e apenas 7 erraram. Isso demonstra uma compreensão substancialmente melhor dos conceitos financeiros abordados, com uma redução notável de erros de 54 para 7, refletindo o efetivo aprendizado durante a utilização do recurso pedagógico.

A terceira questão focou na comparação de números inteiros, em que os alunos completaram lacunas com sinais de maior, menor ou igual.

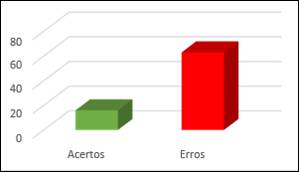
Gráfico 5: Terceira pergunta do pré-teste

No pré-teste (Gráfico 5), a terceira questão revelou dificuldade considerável entre os alunos na comparação de números inteiros. Apenas 16 dos 79 participantes responderam corretamente, enquanto 63 erraram, indicando desafios na interpretação e comparação adequada dos números inteiros apresentados. A maioria dos alunos demonstrou dificuldade em discernir corretamente qual número era maior ou menor (Figura 2).

Figura 2: Resolução dos problemas das cartas retiradas

No pós-teste, houve notável melhora na habilidade dos alunos em compreender a comparação entre números inteiros, com 69 respostas corretas entre os 79 participantes e apenas 10 erros durante o jogo.

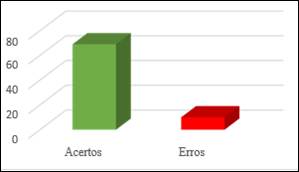
Gráfico 6: Terceira pergunta do pós-teste

Esses resultados evidenciam uma evolução clara no aprendizado dos alunos, demonstrando melhora na habilidade de comparar números inteiros. A redução expressiva no número de erros, de 63 para 10, indica que os alunos assimilaram os conceitos, revelando um progresso substancial no desenvolvimento dessa habilidade matemática fundamental.

A quarta questão do teste exigia que os alunos resolvessem uma adição simples e registrassem o resultado obtido. A expressão apresentada foi (+5) + (+3). Essa questão visava avaliar a competência básica em adição, um conceito essencial em Matemática (Rodrigues, 2009). O objetivo era que os alunos somassem corretamente os números dentro dos parênteses para obter o resultado 8, verificando assim se possuíam um entendimento sólido das operações aritméticas simples para resolver problemas matemáticos mais complexos e realizar cálculos do dia a dia.

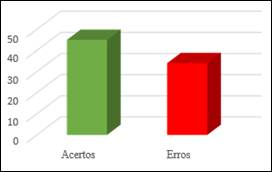
Gráfico 7: Quarta pergunta do pré-teste

Ao analisar a quarta questão, que envolve uma operação de adição, conforme mencionado anteriormente, no pré-teste (Gráfico 7) foram registrados 34 erros e 45 acertos.

No entanto, esse resultado ainda é considerado menos satisfatório, já que a adição envolvia apenas números positivos, geralmente mais compreensíveis para os alunos. Apesar disso, o número significativo de erros aponta desafios na execução correta de operações matemáticas básicas.

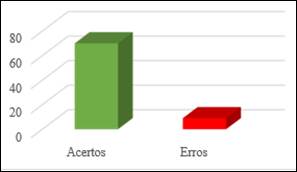
Gráfico 8: Quarta pergunta do pós-teste

No pós-teste (Gráfico 8), os resultados da quarta questão foram muito positivos. Dos participantes, 70 responderam corretamente e apenas 9 erraram. Esse resultado indica um progresso significativo em relação ao pré-teste, demonstrando que o recurso utilizado foi importante para melhorar a compreensão e a execução correta de adições simples com números positivos.

A quinta e última questão do teste envolvia uma operação de subtração: (−7) − (+4). O objetivo era avaliar a habilidade dos alunos em realizar subtrações básicas e interpretar corretamente o resultado (Rodrigues, 2009). Esperava-se que eles compreendessem que subtrair um número positivo de um número negativo resultaria em um número negativo. Nesse caso específico, o resultado correto seria −7 − 4 = −11.

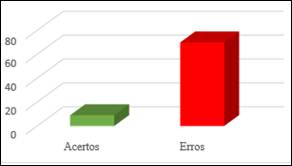
Gráfico 9: Quinta pergunta do pré-teste

Na última questão do pré-teste, que envolvia subtração de números inteiros, a maioria dos alunos enfrentou desafios: 70 erraram, enquanto apenas 9 acertaram. Isso indica dificuldade significativa na compreensão e execução correta de operações de subtração com números inteiros, apontando a necessidade urgente de reforçar os conceitos fundamentais.

Após a explanação inicial do conteúdo e a aplicação do pré-teste, foi perceptível que muitos alunos enfrentavam dificuldades com adição, subtração e comparação de números inteiros. Esses resultados evidenciam a necessidade de intervenção e suporte adicionais durante o aprendizado, destacando a importância de estratégias pedagógicas para aprendizagem dos alunos.

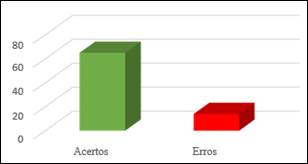
Gráfico 10: Quinta pergunta do pós-teste

No pós-teste (Gráfico 10) da quinta questão, que abordava subtração de números inteiros, 65 alunos responderam corretamente, enquanto 14 erraram.

De modo geral, os dados coletados revelam melhora significativa no desempenho dos alunos após a intervenção. Houve aumento substancial no número de respostas corretas em todas as questões do pós-teste em comparação com o pré-teste, indicando que o jogo Intege Bank foi importante para melhorar a compreensão e a habilidade dos alunos com números inteiros.

Este estudo reforça a importância de métodos de ensino inovadores e destaca o potencial dos jogos educativos para melhorar o processo de ensino-aprendizagem em Matemática, alinhando-se com as ideias de Grando (2000).

A intervenção pedagógica utilizando o jogo Intege Bank está fundamentada nas teorias de Vygotsky (2002) e Kishimoto (2017), que enfatizam o papel crucial dos jogos no desenvolvimento cognitivo e social dos alunos.

Apesar de alguns equívocos, o resultado geral foi positivo, evidenciando melhora na compreensão e na execução das operações de subtração. Isso mostra claramente que o jogo foi importante para ajudar os alunos a entender e aplicar os conceitos matemáticos abordados, destacando a importância de métodos educacionais interativos e inovadores para facilitar o aprendizado de Matemática de forma dinâmica.

Considerações finais

Este estudo se dedicou ao ensino dos números inteiros, um conceito essencial na Matemática, crucial para operações e resolução de problemas variados. O objetivo principal foi avaliar uma estratégia específica para alunos do 7º ano do Ensino Fundamental, utilizando o jogo de cartas Intege Bank para tornar o aprendizado mais interativo.

A análise dos resultados demonstra que o uso do Intege Bank foi altamente benéfico, refletido no aumento dos acertos e na redução nos erros do pré-teste para o pós-teste. Isso evidencia que a abordagem lúdica e interativa facilitou a compreensão dos conceitos de números inteiros, ressaltando a importância de métodos pedagógicos inovadores e adaptados à realidade dos alunos.

A abordagem lúdica e interativa adotada mostrou-se claramente benéfica, facilitando a assimilação de conceitos que poderiam ser considerados abstratos e desafiadores. Assim, o uso de recursos pedagógicos como o Intege Bank deve ser incentivado e amplamente adotado entre os educadores, dada sua promoção do aprendizado mais dinâmico em sala de aula.

No entanto, é importante considerar algumas limitações, como o foco específico em alunos do 7º ano do Ensino Fundamental, o que restringe a generalização dos resultados para outras faixas etárias ou níveis de ensino. Além disso, o estudo concentrou-se em um único recurso pedagógico, indicando a necessidade de explorar e comparar a dinâmica do jogo de diferentes métodos educativos.

Futuras pesquisas poderiam investigar a aplicação de recursos semelhantes em outras áreas da Matemática e em diferentes contextos educacionais, bem como avaliar o impacto a longo prazo dessas estratégias de ensino interativas no desempenho acadêmico dos alunos e na sua atitude em relação à Matemática. Estudos comparativos entre diversos recursos pedagógicos também poderiam fornecer informações valiosas para o desenvolvimento de práticas educacionais mais engajadoras.

Este estudo de caso demonstra a importância do jogo como ferramenta pedagógica para o ensino de números inteiros, enriquecendo a compreensão teórica sobre o ensino de Matemática. Ele oferece um arcabouço prático para educadores, mostrando como a interatividade do jogo facilita a assimilação de conceitos complexos e melhora o desempenho dos alunos, sugerindo o potencial de abordagens lúdicas para outros conteúdos matemáticos.

Referências

CAMPOS, T. M. M. Transformando a prática das aulas de Matemática. São Paulo: Proem, 2001.

CUNHA, M. B. Metodologias para estudo dos usuários de informação científica e tecnológica. Bibliotecon, Brasília, v. 2, nº 10, p. 5-19, 1982.

GAMBOA, S. S. (org.). Pesquisa educacional: quantidade-qualidade. São Paulo: Cortez, 1995.

GRANDO, R. C. O conhecimento matemático e o uso de jogos na sala de aula. 2000. 239f. Tese (Doutorado em Educação) – Universidade Estadual de Campinas, Campinas, 2000.

IFRAH, G. Os números: história de uma grande invenção. 9ª ed. São Paulo: Globo, 1998.

KISHIMOTO, T. M. Jogo, brinquedo, brincadeira e a educação. 14ª ed. São Paulo: Cortez, 2017.

MEDEIROS, A.; MEDEIROS, C. Números negativos: uma história de incertezas. Bolema - Boletim de Educação Matemática, v. 7, nº 8, p. 49-59, 1992.

MILLIES, C. P.; COELHO, S. P. Números: uma introdução à Matemática. 3ª ed. São Paulo: Edusp, 2006.

PRODANOV, C. C.; FREITAS, E. C. de. Metodologia do trabalho cientifico: métodos e técnicas da pesquisa do trabalho acadêmico. 2ª ed. Novo Hamburgo: Ed. Feevale, 2013.

RODRIGUES, R. V. R. A construção e utilização de um objeto de aprendizagem através da perspectiva lógico-histórica na formação do conceito de números inteiros. 2009. 219f. Dissertação (Mestrado em Educação) – Universidade Estadual Paulista, Presidente Prudente, 2009.

SÁ, P. F.; ANJOS, L. J. S. Números negativos: uma trajetória histórica. IX SEMINÁRIO NACIONAL DE HISTÓRIA DA MATEMÁTICA. Anais... Aracaju, 2011.

SAVI, R.; ULBRICHT, V. R. Jogos digitais educacionais: benefícios e desafios. Revista Novas Tecnologias na Educação, v. 6, nº 1, 2008.

SAVIANI, D. Aberturas para a História da Educação: do debate teórico-metodológico no campo da história ao debate sobre a construção do sistema nacional de educação no Brasil. Campinas: Autores Associados, 2023.

SEABRA, J. T. da C. Jogos na construção de projetos pedagógicos para o ensino das quatro operações com números inteiros no 6º ano. 2023. 44f. Trabalho de conclusão de curso (Licenciatura em Matemática) – Universidade Federal do Pará, Castanhal, 2023.

SILVA, M. de O. P. da. Os números e o sistema de numeração decimal: práticas pedagógicas de professores no Brasil e de Portugal. 2020. 203f. Tese (Doutorado em Educação) – Universidade de Sorocaba, Sorocaba, 2020.

SOARES, P. J. O jogo como recurso didático na apropriação dos números inteiros: uma experiência de sucesso. Dissertação (Mestrado em Ensino da Matemática) – Pontifícia Universidade Católica de São Paulo, São Paulo, 2008.

SOUZA, J. N. de; RIBEIRO, Í. C. da S.; SILVA, F. P. da. Um estudo de caso sobre inclusão digital: a importância do uso da tecnologia como ferramenta pedagógica. Revista Educação Pública, v. 24, nº 24, 2024.

SOUZA, R. G. V. de. Uma proposta de sequência didática para o ensino de operações com números inteiros para alunos da EJA. 2019. 81f. Dissertação (Mestrado em Matemática) – Universidade do Estado do Rio de Janeiro, Rio de Janeiro, 2019.

VYGOTSKY, L. S. A formação social da mente: o desenvolvimento dos processos psicológicos superiores. 6ª ed. São Paulo: Martins Fontes, 2002.

ZANARDINI, R. A. D. Um breve olhar sobre a História da Matemática. Curitiba: Intersaberes, 2017.