Trigonometria: aprendizagem significativa com o uso do teodolito no 9º ano do Ensino Fundamental
Joel Bragança Junior
Mestre em Matemática
Arraigados à Educação Matemática estão fortes obstáculos que são enfrentados durante o processo de ensino. Suas matérias são trabalhadas isoladas umas das outras, isto é, sem a interação devida com as demais; dessa forma, os conhecimentos prévios dos alunos acabam sendo desperdiçados ou, se porventura são utilizados, o são de modo mínimo.
Tais conhecimentos poderiam ser mais bem utilizados ao usá-los como um ponto de apoio, visando facilitar a absorção e a concretização do estudo de um novo conteúdo. Este, aliás, é o conceito que Ausubel propõe em sua Teoria da Aprendizagem Significativa. Nessa teoria, Ausubel (2003) afirma que o conhecimento prévio do aluno deve ser usado como ponto de ancoragem para novos estudos, funcionando assim como fator fundamental para a aprendizagem. Essa aprendizagem tem a finalidade de trazer novas ideias para a estrutura cognitiva e fazer com que elas sejam assimiladas às já existentes nela.
A Trigonometria é a área da Matemática responsável pelos estudos das relações entre os lados de um triângulo e seus ângulos. Dentre essas relações, três razões básicas são representadas em um triângulo retângulo: seno, cosseno e tangente. Assim como em outras disciplinas no campo de estudo da Trigonometria, tornou-se costume a aprendizagem de forma automática, sendo superficial a aplicação das razões e relações trigonométricas, sem uma compreensão mais ampla do assunto.
Um aspecto relevante a se destacar é a carência de aplicação prática do conteúdo escolar, salientado por tornar a Matemática mais abstrata. Esses pontos, então, dão origem a um grande desafio enfrentado pelo professor: buscar diferentes métodos pedagógicos para encarar e solucionar essa situação. Vygotsky (2007), em sua teoria do interacionismo, aponta que é preciso um meio social para a formação de estruturas cognitivas essenciais para o desenvolvimento do indivíduo. Dessa forma, a aprendizagem se dá pela interação do sujeito com o objeto estudado, seja ele físico ou abstrato.
Com base nisso, a proposta é empregar instrumentos lúdicos nas aulas de Trigonometria no 9° do Ensino Fundamental, instrumentos que sejam comuns ao aluno e que tenham real significância para ele, caso contrário o aprendizado não teria significado, sendo apenas recurso para a memorização. Na Trigonometria, são diversos os instrumentos que podem ser utilizados para a medição de ângulos; um deles é o teodolito. Este, em especial, tem sua construção simples e pode ser utilizado em qualquer local, o que o torna um excelente objeto para ser montado e usado em sala de aula.
Neste estudo, iremos explorar conceitos fundamentais da construção cognitiva, a formação de conhecimento significativo e a importância dos subsunçores. Além disso, analisaremos o papel do mediador nesse contexto. Também discutiremos as vantagens do uso de materiais lúdicos no processo de aprendizagem e exploraremos a construção de um teodolito como parte desse processo.
O principal objetivo é desenvolver um projeto de ensino da Trigonometria fundamentado nas teorias de Vygotsky e, principalmente, Ausubel. Neste projeto, buscamos criar um ambiente de aprendizado que permita aos alunos construir significados sólidos e duradouros na área da Trigonometria, aproveitando ao máximo os recursos disponíveis e promovendo uma compreensão mais profunda do assunto.
Materiais e métodos
A pesquisa bibliográfica voltada à aprendizagem lúdica significativa da Trigonometria no 9° ano do Ensino Fundamental buscou apresentar pontos e características comuns aos teóricos estudados em consideração às observações feitas em sala de aula, tanto do ponto de vista do aluno quanto do professor/mediador. A fim de compreender a visão de cada teórico, é necessário considerar o ambiente e a sociedade da época, pois são aqueles os referenciais que proporcionaram idealizar algo; além do mais, necessita-se atualizar os valores da atual sociedade para que os ideais construídos por eles possam ser adequados aos novos tempos.
A fim de tornar prático o aprendizado trigonométrico, sempre foi levada em consideração a importância de o objeto de estudo estar acessível ao aluno, de preferência em seu cotidiano, facilitando assim a significação do conteúdo por seu conhecimento escolar e empírico. Deve ser, portanto, prioridade a aplicação lógica e prática da disciplina, transpondo as linhas do caderno, as paredes da sala de aula, a criatividade do professor e a imaginação de cada aluno.
Para tal aprendizado, foi adotado como instrumento principal de estudo o teodolito, que, juntamente com outras ferramentas lúdicas, auxilia o desenvolvimento e o aprendizado significativo, a fim de proporcionar aos alunos a construção desse conhecimento de maneira empírica. Assim, os alunos podem observar e tomar suas conclusões a cada passo dado nessa construção, o que é fundamental para o processo, já que a imaginação do discente é uma ferramenta e deve estar presente a todo instante em meio escolar – caso contrário, o material lúdico terá sua função prejudicada.
Aprendizagem Significativa I
Uma das maiores dificuldades dos alunos no atual modelo de ensino é coligir as disciplinas umas com as outras e integrar os conteúdos de uma mesma disciplina, o que é um empecilho para propostas interdisciplinares e intradisciplinares. Essa dificuldade é ainda mais comum no campo das Ciências Exatas – neste caso, a Matemática –, já que a necessidade e a relação entre as disciplinas da matéria e o raciocínio lógico são essenciais para seu desenvolvimento.
A aprendizagem mecânica se fez em muitos casos parte ativa da Matemática, tornando-se um erro anacrônico, porém reversível. Um exemplo é substituir valores no Teorema de Pitágoras ao invés de compreender as relações entre suas razões. Para tal, o aluno deve deixar de ser apenas um “recipiente vazio” e o professor se tornar um orientador e mediador do conhecimento para que o discente possa participar ativamente da construção de seu conhecimento, desenvolvendo, além do conhecimento específico, o conhecimento crítico, que é fundamental para dar significação ao aprendizado (Jesus, 2013).
Segundo Ausubel (2003), o conhecimento significativo sustenta-se quando se estabelece uma relação substantiva e não arbitrária entre as novas relações e um aspecto relevante da estrutura de conhecimentos. Os subsunçores são os fatores de maior relevância no aprendizado significativo; sem eles, resta ao aluno a memorização. O aprendizado significativo pode ser considerado ativo, já que começa pela identificação de um conhecimento previamente adquirido. Consequentemente ocorre a reconciliação integrativa, que é apreensão de similaridades e diferenças, nela encontram-se contradições reais ou aparentes entre si, fazendo com que sejam formadas novas proposições e/ou outras antigas sejam alteradas, tendo em mente que essa relação é particular a cada aluno.
A aprendizagem significativa ocorre quando a nova informação adquirida "ancora-se" em conceitos relevantes previamente existentes na estrutura cognitiva do aprendiz. Nesse processo, a nova informação interage com uma estrutura de conhecimento específica, que Ausubel chama de "conceito subsunçor", ou "subsunçor". Ela é progressiva, pois vamos aprendendo e dando significado às coisas. A interação (palavra-chave) entre conhecimentos novos e prévios é a característica chave da aprendizagem significativa (Moreira, 1999, p. 46).
Ausubel (2003) não descarta o aprendizado mecânico — memorístico —, ressalvando que ele deve ser usado somente quando a estrutura cognitiva do aluno não possuir subsunçores (pontos de ancoragem), já que esse modelo de aprendizado possui grau de retenção de conhecimento baixíssimo em médio e longo prazo. A ausência de subsunçores que ancorem o aprendizado justifica o aprendizado mecânico apenas do conhecimento inicial. Ausubel sugere que esse conhecimento inicial possa ser utilizado como âncora num processo de diferenciação progressiva que estrutura paulatinamente o conhecimento sobre determinado assunto.
Aprendizagem Significativa II
Na corrente interacionista, o processo de aprendizagem é sempre dinâmico, com o sujeito interagindo junto ao objeto de estudo, que pode ser físico (objeto) e abstrato — simbólico — (crenças, valores e costumes). Vygotsky (2007) afirma que esses objetos são os responsáveis pela elaboração de estruturas cognitivas e fundamentais para o desenvolvimento do ser humano, haja vista que o sujeito não possui acesso direto a esses objetos, pois são dispostos pelo sistema de símbolos de que dispõe. Sendo assim, cabe à cultura fornecer a tais indivíduos os símbolos que representam sua realidade.
Assim, fica claro que a construção cognitiva parte de fora para dentro do indivíduo, com a cultura sendo parte integrante do processo. O interacionismo se torna socioconstrutivismo quando se relaciona aos fatores base do ideal de Lev Vygotsky. Nascido na Bielorrússia (mais tarde parte da União Soviética), Vygotsky foi bastante influenciado por ideias socialistas — tanto que seus pensamentos são conceituados em Marx e Engels, e, na melhor tradução desses sociólogos, o mecanismo de mudança individual ao longo do desenvolvimento tem sua raiz na sociedade, na cultura e na história. Assim, pode-se eliminar a ideia de que o desenvolvimento cognitivo parta apenas da estrutura biológica; é necessária interação com o meio. Teresa Cristina Rego (1999, p. 98) afirma sobre a teoria de Vygotsky:
Em síntese, nessa abordagem, o sujeito produtor de conhecimento não é um mero receptáculo que absorve e contempla o real nem o portador de verdades oriundas de um plano ideal; pelo contrário, é um sujeito ativo que em sua relação com o mundo, com seu objeto de estudo, reconstrói (no seu pensamento) este mundo. O conhecimento envolve sempre um fazer, um atuar do homem.
A teoria Vygotskiana é baseada em três pilares de estudo:
- Primeiro pilar: as funções psicológicas possuem suporte biológico (atividades cerebrais). Assim, mesmo se tratando de uma teoria interacionista, não se descarta a importância das funções biológicas, como as atividades cerebrais.
- Segundo pilar: o funcionamento psicológico se desenvolve a partir das relações entre o indivíduo e o meio externo.
- Terceiro pilar: a relação entre homem e mundo é mediada por símbolos, por exemplo: a linguagem (fala, escrita e leitura). Assim, permite-se maior e melhor apreensão da realidade pelo indivíduo.
O desenvolvimento do aluno dar-se-á do pensamento elementar, com nível de heteronomia (dependência do professor) muito grande, para um pensamento superior, que apresenta comportamento intencional, ou seja, próprio do aluno. Esse desenvolvimento ou aprendizagem é denominado a princípio zona do desenvolvimento proximal, que é a influência do professor sobre o aluno; zona de desenvolvimento real, que é a capacidade momentânea do aluno; e, por último, zona de desenvolvimento potencial, que é aonde ele pode chegar.
O uso de meios artificiais — a transição para a atividade mediada — muda, fundamentalmente, todas as operações psicológicas, assim como o uso de instrumentos amplia de forma ilimitada a gama de atividades em cujo interior as novas funções psicológicas podem operar. Nesse contexto, podemos usar o termo função psicológica superior ou comportamento superior com referência à combinação entre o instrumento e o signo na atividade psicológica (Vygotsky, 2007, p. 56).
O maior problema na busca pela compreensão das atividades psicológicas é o método utilizado, que influencia diretamente a aprendizagem significativa. Isso ocorre porque, inicialmente, o método é um pré-requisito que desempenhará papel crucial no resultado final, atuando como instrumento e determinando o resultado com base no desenvolvimento cognitivo do aluno (Vygotsky, 1988).
Trigonometria
Trigonometria são as relações entre os lados de um triângulo retângulo, dadas aqui, a partir de concepções e fatos ligados ao cotidiano, já que seu surgimento se deu como consequência de necessidades práticas, principalmente ligadas à Astronomia, à agrimensura e à navegação. Por meio dela, a Matemática se torna o melhor instrumento para o entendimento de fenômenos naturais.
Desde a Antiguidade e até hoje, o homem sempre teve a necessidade de avaliar distâncias inacessíveis. Na verdade, são muito poucas as distâncias que podem ser medidas diretamente – com uma trena, por exemplo. Praticamente tudo que desejamos saber sobre distâncias no mundo em que vivemos é calculado com o auxílio da Trigonometria (Lima et al., 2003, p. 64).
Sempre houve necessidade de medir. Por vezes, essa medição conflitava com fatores físicos e a falta de ferramentas, tornando-se medidas inacessíveis para o ser humano – como a altura de uma árvore, ou a largura de um rio. Entretanto, por meio das relações trigonométricas conseguimos determinar esses valores.
No 9° ano do Ensino Fundamental, uma parte da Trigonometria não é aplicada devido à sua pouca utilização naquele contexto escolar. Esse conteúdo, então, pode ser substituído por novos exercícios trigonométricos que se encaixam no perfil do nível de ensino. Um ponto relativamente importante no estudo da Trigonometria são as relações de seno e cosseno, que devem ser constantemente aplicadas e compreendidas de três maneiras.
Essas relações podem ser expressas em forma de razões, utilizando ângulos agudos de um triângulo retângulo; podem ser visualizadas no contexto do círculo trigonométrico, onde os valores seno e cosseno são representados como coordenadas de pontos no círculo unitário; e podem ser abordadas como funções trigonométricas, geralmente denotadas por SEN, COS e TAN. É fundamental dominar essas diferentes perspectivas, pois elas desempenham papel crucial na resolução de problemas trigonométricos e na compreensão das relações entre ângulos e lados em triângulos, sendo essenciais para um estudo completo e eficaz da Trigonometria.
Algumas informações valiosas, como a semelhança de triângulos estudada por Tales de Mileto, devem ser conhecidas pelos alunos. Esses conhecimentos históricos e matemáticos não apenas enriquecem sua bagagem como também proporcionam um contexto relevante para o estudo da Trigonometria.
Ao apresentar tais informações, os estudantes podem compreender a trajetória do desenvolvimento desse campo ao longo da história e, mais importante ainda, relacionar a importância de cada ângulo e sua função no contexto da semelhança de triângulos. Isso amplia sua perspectiva e aprofunda a apreciação pela disciplina, evidenciando como descobertas antigas continuam fundamentais para a compreensão moderna da Trigonometria.
No triângulo retângulo, é possível notar e demonstrar essa relação usando os catetos e a hipotenusa, analisando os princípios da disciplina. Ao iniciar um novo processo — razões trigonométricas no círculo trigonométrico — o aluno assimila o novo conceito com o conhecimento já adquirido, tornando-se este um fator importante para novas aprendizagens e para um estudo realmente significativo (Viganó; Lima, 2015).
Se a estrutura cognitiva for clara, estável e bem organizada, surgem significados precisos e inequívocos, e estes têm a tendência de reter a força de dissociabilidade ou disponibilidade. Se, por outro lado, a estrutura cognitiva for instável, ambígua, desorganizada ou organizada de modo caótico, tem tendência a inibir a aprendizagem significativa e a retenção. Assim, é através do fortalecimento de aspectos relevantes da estrutura cognitiva que se pode facilitar a nova aprendizagem e retenção (Ausubel, 2003, p. 10).
Ao analisar o círculo trigonométrico, é possível o aluno “enxergar” as relações entre as retas (ângulos) do estudo anterior. Nesse instante, uma nova proposição passa a ser criada pelo aluno, dando assim significação ao primeiro estudo de caso. É importante que possa entender o significado de π e relacionar uma nova medida, chamada de radiano, aos graus.
Os fundamentos das leis dos Senos e dos Cossenos tiveram suas primeiras demonstrações nas razões trigonométricas, passando pelo círculo até chegar ao resultado final. Por mais que tenha sido fundamentada no Teorema de Pitágoras, essas relações são aplicadas a quaisquer triângulos, diferenciando apenas o número de ângulos e lados conhecidos deles para definir a relação a ser utilizada: caso saibamos dois ângulos e um lado, usamos a Lei dos Senos; caso saibamos dois lados e um ângulo, usamos a Lei dos Cossenos (Costa, 1997).
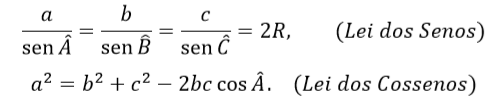
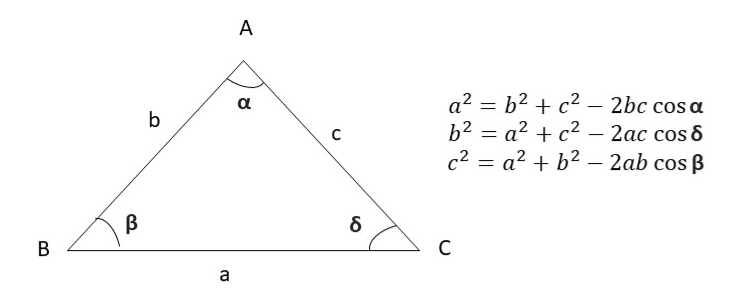
Figura 1: Representação da Lei dos Senos no triângulo
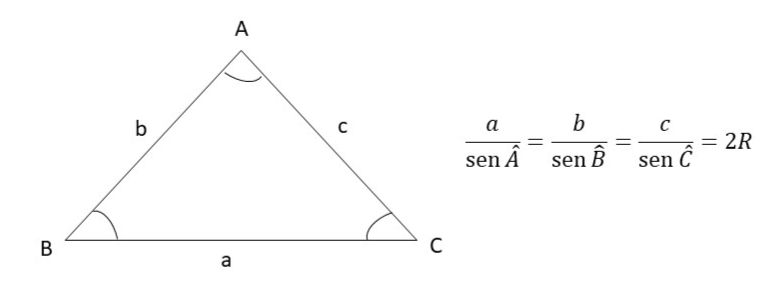
Figura 2: Representação da Lei dos Cossenos no triângulo
Vale ressaltar que é importantíssimo seguir as orientações curriculares dispostas na BNCC, haja vista que todo o método aqui disposto abrange os descritores referentes ao 9° ano do Ensino Fundamental relacionado ao ensino da Trigonometria.
Materiais lúdicos
A princípio, deve-se ter em mente que os materiais lúdicos não devem ser utilizados por parte do professor com o pressuposto de o aluno atingir somente a nota necessária para aprovação. Esse tipo de material deve ser compatível com a estrutura cognitiva prévia do aluno, a fim de que ocorra interesse pelo conteúdo, potencializando assim uma aprendizagem com significação. Portanto, não se deve confundir o aprendizado significativo com o aprendizado de material significativo, pois, se o conhecimento transmitido por meio desse material não tiver significância, passará a ser decorado, diferentemente de uma aprendizagem representacional, que tem para o aprendiz significado, seja ele qual for, que os referentes possuem.
Aprender não é primeiramente memorizar, estocar informações, mas reestruturar seu sistema de compreensão de mundo. Tal reestruturação não acontece sem um importante trabalho cognitivo. Engajando-se nela, restabelece-se um equilíbrio rompido, dominando melhor a realidade de maneira simbólica e prática (Perrenoud, 2000, p. 30).
No âmbito trigonométrico, pode-se notar instrumentos que se enquadram nas prerrogativas anteriores, como o teodolito, astrolábio, oitante, vicmetro. Como Santos et al. (2012) notam, o teodolito é um instrumento simples e de fácil construção que tem como função medir principalmente ângulos, sejam eles na posição horizontal ou vertical; as medições na posição horizontal são mais precisas por questões instrumentais relacionadas à ferramenta. A aplicação desse instrumento pode ser realizada em qualquer ambiente, graças à sua ampla funcionalidade e praticidade.
Estes são os materiais necessários para sua construção:
- Canudo oco em formato cilíndrico reto (o buraco interno deve ter diâmetro de forma suficiente para visualizar o outro lado);
- 1 transferidor de grau;
- 1 pedaço de papelão de 15cm × 14cm;
- 1 pedaço de papelão de 10cm × 14cm;
- 1 pedaço de papelão em forma de um triângulo retângulo de 9cm × 9cm;
- Cola;
- Régua;
- 1 parafuso;
- 1 tampa de refrigerante.

Figura 3: Materiais para construção do teodolito
A construção se dá da seguinte forma:
Passo 1: O primeiro passo para a construção do teodolito é recortar os pedaços de papelão.
Passo 2: Em seguida, cole os pedaços de papelão conforme a Figura 4.


Figura 4: Colagem dos pedaços de papelão
Passo 3: Cole o transferidor de grau no papelão.

Figura 5: Colagem do transferidor de grau
Passo 4: Fure o centro e as laterais e fixe a tampa de refrigerante no papelão no centro do transferidor de grau.

Figura 6: Fixação da tampa do refrigerante no papelão
Passo 5: Coloque o canudo nos furos da tampa de refrigerante.

Figura 7: Fixação do canudo na tampa de refrigerante
Encontre um local para posicionar o teodolito – uma mesa, por exemplo. Em seguida, basta escolher um ponto qualquer cuja altura se queira saber e, então, localizá-lo olhando através do canudo — certificando-se de que o eixo do transferidor esteja paralelo ao chão. Após encontrar o ponto referencial, analise o ângulo indicado no transferidor pelo arame; esse será o seu ângulo. Com a trena, meça a distância entre o transferidor e o local sob o ponto (formando um ângulo de 90°). Utilizando a relação da tangente, encontramos parte da altura. Então, some ao valor encontrado a medida da altura da mesa; assim, será encontrada uma medida aproximada do ponto escolhido.
O teodolito acaba sendo um perfeito exemplo do poder da disciplina Matemática, já que se trata de um instrumento multiuso, assim como a disciplina, que contém um conteúdo muito específico, além do fato de estar presente na grande maioria das demais, como Física, Química, Biologia. Em dados momentos são requisitados ao aluno conceitos que não se desenvolvem nessas áreas, mas sim na Matemática, por exemplo: cálculo da probabilidade de um evento genético ocorrer; cálculo da velocidade média de um corpo; e, até mesmo nas reações químicas, a quantidade (massa) de cada elemento químico para realizar tal experimento. Por esses motivos, torna-se ainda mais importante o interesse do aluno nas aulas de Matemática, pois em seu currículo acadêmico ela se torna interdisciplinar.
Os educadores matemáticos deveriam procurar alternativas para aumentar a motivação na aprendizagem desenvolvendo a autoconfiança, a organização, a concentração, estimulando a socialização e aumentando as interações do indivíduo com outras pessoas (Oliveira, 2007, p. 5).
Essa “facilidade e praticidade” por vezes esbarra na própria formação do educador, que traz consigo marcas muitos fortes de uma formação pedagógica liberal tradicional; aqueles que acompanham o desenvolvimento intelectual e tecnológico conseguem se adaptar, e os que não conseguem acabam se colocando no falecimento acadêmico. “O abandono da Matemática traz dano a todo conhecimento, pois aquele que a ignora não pode conhecer as outras ciências ou as coisas do mundo” (Bacon, 1980).
Resultados e discussão
Por diversas vezes, nota-se o equívoco ao consubstanciar informação e conhecimento. Informação deve ser o ponto de partida para construção do conhecimento, e esse conhecimento, por sua vez, deve ser significativo, caso contrário com o passar do tempo regredirá novamente a apenas uma informação. O principal responsável por diferenciá-los em sala de aula — informação vs. conhecimento — é o professor, pois dependerá de como serão ministradas suas aulas, se elas terão ou não referenciais teóricos, se haverá aplicação no cotidiano e principalmente se o docente estará disposto a transformar a informação que o aluno possui em conhecimento.
Partindo do conceito de Vygotsky (2007), de pensamento elementar para pensamento superior, tendo em vista o papel de mediador do conhecimento para um aluno, ou seja, sendo um referencial, deve-se utilizar os conceitos geométricos adquiridos no decorrer do Ensino Fundamental juntamente aos de Álgebra, pois são as únicas “informações” de que os discentes dispõem para construção do novo conhecimento, que são as razões trigonométricas. Nesse ponto, a aplicação do teodolito (ou outro objeto) como material lúdico irá acrescentar-se ao conhecimento do aluno, tendo em vista que não irá substituir o modo de como esses conceitos foram transmitidos, e sim apresentar novos caminhos para tal fato.
Um conhecimento só é pleno se for mobilizado em situações diferentes daquelas que serviram para lhe dar origem. Para que sejam transferíveis a novas situações e generalizados, os conhecimentos devem ser descontextualizados, para serem novamente contextualizados em outras situações (Brasil, 1998, p. 36).
Por vezes, depara-se com alunos que em algum momento de sua vida acadêmica não apreenderam determinado conteúdo. Este, à vista disso, deve ser retomado a fim de proporcionar um novo modelo de compreensão. Em outras palavras, o professor deve criar elos entre os conteúdos para que o aluno possa ter a devida significação da matéria, pois uma vez que se perde uma parte dessa estrutura é inevitável a perda ou dificuldade noutras matérias posteriores que venham a utilizar tais conteúdos. E é justamente nesse ponto que o lúdico entra em ação, pois ele é responsável pela quebra de um sistema de ensino tradicional e não significativo, buscando alternativas e caminhos que irão justapor ideias e até mesmo mudando o comportamento do aluno, aumentando assim a interação social (Oliveira, 2007).
Considerações finais
As primeiras abordagens e a dedução de conceitos trigonométricos do 9° ano do Ensino Fundamental são triviais para o restante da jornada escolar estudantil, seja ela em outras disciplinas no Ensino Médio ou no Ensino Superior. Isso se dá devido à utilização da disciplina, abrangendo diversas diretrizes, como o Cálculo que é utilizado em várias áreas, como Engenharia, Astronomia, Física e Matemática.
Foi apresentada uma proposta de ensino para Trigonometria baseada nos conceitos de Ausubel, valorizando o conhecimento anterior já adquirido, e os pilares de Vygotsky, com interacionismo e a transformação de conhecimento elementar em conhecimento superior, sabendo que num ciclo o conhecimento superior se dará após o conhecimento elementar. Sendo assim, a construção do conhecimento significativo é um processo cíclico ou, na melhor das hipóteses, em cadeia, já que nunca se descartam ou excluem conceitos formados e ancorados outrora.
No geral, a potencialidade da aprendizagem lúdico-significativa vem sendo estudada cada vez mais. Um processo tradicional é descartado em todos os níveis de ensino, e a utilização de material lúdico para a significação de conteúdos surge para eliminar de vez o modelo arcaico de ensino. É notória a efetividade de meios lúdicos quando o aluno se dispersa da aula, muitas vezes por motivos fúteis, pelo simples fato de estar entediado e cansado da metodologia do professor.
Chega-se à conclusão inequívoca da importância crítica de como cada conceito é transmitido e dos métodos empregados para essa finalidade. A base dessa abordagem deve ser a busca incessante por uma aprendizagem que seja realmente significativa, evitando a simples memorização mecânica. Isso implica conectar o que aprendemos às situações do dia a dia, relacionar os novos conhecimentos ao que já dominamos e enriquecer o aprendizado por meio da utilização de materiais lúdicos e envolventes.
Esses elementos não são meramente complementares, mas sim os alicerces essenciais para uma educação de excelência. Eles não apenas enriquecem o processo de ensino-aprendizagem, mas também estimulam a participação ativa e a motivação dos alunos, tornando o aprendizado mais aprofundado e eficaz. Portanto, é incontestável que a função do educador transcende a simples transmissão de informações; ela envolve a criação de um ambiente de aprendizado inspirador, em que o conhecimento se torna uma ferramenta poderosa para o crescimento e o desenvolvimento dos estudantes.
Referências
AUSUBEL, David Paul. Aquisição e retenção de conhecimentos: uma perspectiva cognitiva. Trad. Lígia Teopisto. Lisboa: Paralelo, 2003.
BACON, Roger. Doctor Mirabilis (Doutor Admirável). Filósofo Inglês com ênfase em Empirismo e ao uso da Matemática no estudo da natureza (1214-1294). In: Grande Enciclopédia Universal. Amazonas, edição 1980.
BARROSO, J. M. (ed.). Matemática: construção e significado. São Paulo: Moderna, 2005.
BRASIL. Ministério da Educação. Secretaria da Educação Básica. Orientações Curriculares para o Ensino Médio. Vol. 2. Brasília: MEC, 2006.
BRASIL, Ministério da Educação e do Desporto. Secretaria da Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC, 1998.
BRASIL. Ministério da Educação. Secretaria de Educação Média e Tecnológica. Parâmetros Curriculares para o Ensino Médio. Brasília: MEC, 1999.
COSTA, Nielce M. Lobo. A história da Trigonometria. 1997. 118f. Dissertação (Mestrado em Matemática) – Pontifícia Universidade Católica, São Paulo, 1997.
JESUS, Nadson Lima. A Aprendizagem Significativa em Trigonometria sob o ponto de vista de quem ensina e de quem aprende. Canoas, 2013.
LIMA, Elon Lages et al. Temas e problemas. 3ª ed. Rio de Janeiro: Sociedade Brasileira de Matemática, 2003. Coleção do Professor de Matemática.
MOREIRA, Marco Antônio. Teorias de aprendizagem. São Paulo: EPU, 1999.
OLIVEIRA, Sandra Alves de. O lúdico como motivação nas aulas de Matemática. Mundo Jovem, nº 377, p. 5, jun. 2007.
PERRENOUD, P. Dez novas competências para ensinar. Porto Alegre: Artmed, 2000.
REGO, T. C. Vygotsky: uma perspectiva histórico-cultural da Educação. Petrópolis: Vozes, 1999.
SANTOS, Eunice Moreira et al. O uso do teodolito como metodologia de ensino-aprendizagem de razões trigonométricas. Dourado, 2012.
VIGANÓ, Vanessa Cristina Rech; LIMA, Isolda Gianni de. Aprendizagem Significativa de Trigonometria. Remat, Caxias do Sul, v. 1, nº 2, 2015.
VYGOTSKY, Lev S. A formação social da mente. 7ª ed. São Paulo: Martins Fontes, 2007.
VYGOTSKY, Lev Semenovich. Aprendizagem e desenvolvimento intelectual na idade escolar. In: VIGOTSKY, Lev Semenovich; LURIA, Alexander Romanovich; LEONTIEV, Alexis N. Linguagem, desenvolvimento e aprendizagem. Trad. Maria da Penha Villalobos. 2ª ed. São Paulo: Ícone, 1988. p. 103-117.
Publicado em 17 de setembro de 2025
Como citar este artigo (ABNT)
BRAGANÇA JUNIOR, Joel. Trigonometria: aprendizagem significativa com o uso do teodolito no 9º ano do Ensino Fundamental. Revista Educação Pública, Rio de Janeiro, v. 25, nº 35, 17 de setembro de 2025. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/25/35/trigonometria-aprendizagem-significativa-com-o-uso-do-teodolito-no-9-ano-do-ensino-fundamental
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

