Aprendizagem e animação 3D no Tinkercad: um estudo sobre sólidos geométricos à luz dos critérios de idoneidade didática
Gabriele Silva Carneiro Batista
Doutoranda (PPGen/UESB - câmpus Vitória da Conquista), professora no Colégio da Polícia Militar Eraldo Tinoco
Marisa da Silva Araújo
Doutoranda (PPGen/UESB - câmpus Vitória da Conquista, professora da rede municipal no Colégio Valeriana Rosa Cesar, em Serra/ES
Professores buscam constantemente inovações que promovam o aprendizado dos estudantes, e o uso de materiais didáticos visuais e manipuláveis contribui significativamente para esse processo. A utilização de plataformas 3D é uma possibilidade para o ensino de matemática, como destaca Moran (2015), pois elas ampliam as capacidades de aplicação da matemática ao cotidiano dos estudantes.
Este trabalho aborda o uso do Tinkercad da Autodesk®, uma plataforma online gratuita de modelagem tridimensional, acessível e prática, destacando seu recurso Code Blocks, que permite a criação de animações sem necessidade de conhecimentos avançados em programação.
A proposta envolveu a tarefa Modelando Sólidos Geométricos, permitindo aos estudantes construírem protótipos virtuais com base nos estudos dos sólidos geométricos, analisados à luz dos critérios de idoneidade didática (CID). A realização da atividade promoveu uma interação lúdica e significativa, tanto para o professor quanto para o estudante, com os conceitos da geometria espacial.
O trabalho seguiu as orientações da Associação Brasileira de Normas Técnicas (ABNT, 2000), que apresenta um documento específico visando explicitar as normas para a utilização das tecnologias digitais na educação. Entre essas normas, destacam-se aquelas relacionadas a animações gráficas, que, segundo Muniz (2010), são mecanismos capazes de oportunizar ao aprendiz o desenvolvimento de habilidades que favoreçam sua aprendizagem.
Nessa perspectiva, a pesquisa buscou responder à seguinte questão: quais as contribuições e desafios percebidos pelos estudantes ao realizarem tarefas matemáticas em uma plataforma de animação gráfica seguindo os critérios de idoneidade didática?
Buscando responder à questão proposta, a pesquisa teve por objetivo analisar o desenvolvimento da percepção do aprendiz a partir das contribuições e desafios identificados durante a utilização de tarefas matemáticas desenhadas para uso em plataforma de animação gráfica, com base nos critérios de idoneidade didática.
Ensino e animação gráfica no Tinkercad
No ensino, a animação se destaca por apresentar grande potencial ao tornar os conteúdos mais organizados, atrativos e de fácil interpretação, contribuindo para a construção de conceitos. Segundo Novaes (2020), recursos visuais animados podem ser entendidos como produtos educacionais que ilustram e consolidam a aprendizagem.
Isto posto, a utilização de animações em aula pelo professor proporciona um ensino mais dinâmico, compartilhado e contextualizado, oportunizando melhor desempenho em ambientes tecnológicos. Toscani et al. (2018) ressaltam que essas ferramentas facilitam a resolução de situações-problema mais complexas. Nunes (2018) enfatiza que, com o desenvolvimento das mídias digitais, em muitos casos houve a substituição de técnicas tradicionais, como o desenho manual, pela utilização de ilustrações e animações digitais, permitindo maior agilidade na produção dessas animações. Outro advento marcante nesse processo evolutivo foram as animações 3D, que possibilitaram a criação de apresentações dinâmicas nunca antes vistas pelas pessoas.
No entanto, Novaes (2020) também destaca que o uso de animações no campo educacional não deve ter a pretensão de substituir a atuação do professor, mas complementar os recursos já utilizados em aula, colaborando com os processos de ensino e aprendizagem.
Para Moreira (2016), os modelos tridimensionais permitem uma aproximação entre a parte conceitual e a apreensão tátil, criando um conjunto de significados que dialogam entre si, favorecendo a retenção e a transferência do conhecimento. Já Bandeira et al. (2019) defendem que o uso da plataforma Tinkercad colabora para o protagonismo do estudante no processo de aprendizagem, alinhando-se aos princípios da educação do século XXI.
Os critérios de idoneidade e percepções didáticas
Os critérios de idoneidade didática (CID), fundamentados no modelo teórico do enfoque ontossemiótico do conhecimento e da instrução matemática (EOS), foram utilizados como base para o desenho e avaliação das tarefas empregadas neste estudo, buscando identificar práticas que favoreçam a aprendizagem e que possibilitem melhorar os processos de ensino e aprendizagem, reestruturando-os, configurando-se, desse modo, como instrumento para uma didática normativa (Font; Planas; Godino, 2010).
De acordo com Gusmão e Font (2020) e Godino et al. (2013), os seis critérios são:
- Idoneidade epistêmica: grau de representatividade dos significados institucionais implementados (ou pretendidos) em relação ao significado de referência;
- Idoneidade cognitiva: grau em que os significados pretendidos/implementados estão na zona de desenvolvimento proximal dos alunos, assim como a proximidade dos significados pessoais alcançados aos significados pretendidos/implementados;
- Idoneidade interacional: grau em que as configurações e trajetórias didáticas permitem, por um lado, identificar conflitos semióticos potenciais e, por outro, resolver conflitos que forem produzidos durante o processo de instrução mediante a negociação de significados;
- Idoneidade mediacional: grau de disponibilidade e adequação dos recursos materiais e temporais necessários para o desenvolvimento do processo de ensino e aprendizagem;
- Idoneidade emocional: grau de implicação (interesse, motivação) do alunado no processo de estudo;
- Idoneidade ecológica: grau de adaptação do processo de estudo ao projeto educativo da escola, às diretrizes curriculares e às condições do entorno social.
Godino (2013) ressalta que esses critérios, embora úteis, demandam indicadores empíricos dada sua complexidade. Nessa perspectiva, Godino et al. (2006) disponibilizam um conjunto de indicadores empíricos que auxiliam na análise e avaliação da qualidade didática. Assim, este estudo adota os critérios mediacional e emocional, por explorarem recursos digitais e promoverem aprendizagens contextualizadas à vida cotidiana e profissional dos estudantes.
A análise apresentada nas seções seguintes busca evidenciar esses critérios por meio de indicadores observáveis que permitam avaliar a adequação das tarefas propostas.
Aspectos metodológicos
Este estudo de campo qualitativo visa compreender as particularidades de uma situação educacional real envolvendo estudantes em seu ambiente de aprendizagem. Segundo André (2006), pesquisas qualitativas procuram novos conceitos e formas de entender a realidade, tendo como principal característica o processo natural das ações, dentro de um plano aberto e flexível.
Nesse sentido, buscamos a pesquisa de campo, que, de acordo com Gil (2008), valoriza a interação entre os sujeitos de grupos ou comunidades específicos, permitindo maior profundidade investigativa. O planejamento é mais flexível e pode continuar mesmo que os objetivos sejam modificados no decorrer da pesquisa.
A prática aconteceu no Colégio da Polícia Militar Eraldo Tinoco no ano letivo de 2022, em que aplicamos uma tarefa digital elaborada pela professora tutora da turma, utilizando os recursos de animações gráficas do Tinkercad, disponível em: https://www.tinkercad.com. Nesse cenário, a possibilidade de descobrir a emoção de inventar, misturar, combinar, depurar e aprender oferece pressupostos básicos, como a ideia de que o estudante aprende fazendo, ou seja, a partir da manipulação e visualização de objetos e de atividades práticas.
O estudo foi desenvolvido com a turma do 1° ano C dos Itinerários Formativos de Exatas, por meio de uma tarefa digital elaborada pela professora tutora, utilizando a plataforma Tinkercad. Vale salientar que a principal função dos Itinerários Formativos é proporcionar ao estudante o aprofundamento das aprendizagens que mais se aproximam de seu perfil, aptidão e interesse, valorizando também seu protagonismo e autonomia, conforme previsto na BNCC (Brasil, 2018).
Para a produção de dados, foram utilizadas a observação e entrevistas semiestruturadas. Durante as aulas de Matemática, o pesquisador, além de ver e ouvir, registrou os acontecimentos relevantes, conforme Triviños (1987), que define a observação como um processo atento e intencional. Para o autor, é necessário que o fenômeno seja especialmente separado do seu contexto para que se possa estudar suas ações, tarefas, definições, afinidades e relações.
As entrevistas foram realizadas com 27 estudantes, partindo de questionamentos considerados básicos e se ampliando conforme as respostas dos participantes. Assim, “o informante, seguindo espontaneamente a linha de seu pensamento e de suas experiências dentro do foco principal colocado pelo investigador, começa a participar na elaboração do conteúdo da pesquisa” (Triviños, 1987, p. 146).
Privilegiou-se a entrevista semiestruturada na investigação, pois, como afirma Triviños (1987), ela valoriza a presença do pesquisador ao mesmo tempo que oferece todas as perspectivas possíveis para que o entrevistado alcance a liberdade e espontaneidade necessárias, enriquecendo a investigação. Os relatos foram transcritos, separando alguns trechos considerados relevantes para a descrição e análise dos dados.
Para a análise das entrevistas, escolheu-se o método da Análise de Conteúdo abordado por Bardin (2009, p. 40), que consiste em “um conjunto de técnicas de análises das comunicações, visando obter, por procedimentos sistemáticos e objetivos, a descrição do conteúdo das mensagens”.
O processo consistiu na seleção de indicadores que permitiram a inferência de conhecimentos relativos às condições de produção e recepção das mensagens, sendo que todos os fatos foram vivenciados pelas pesquisadoras durante a investigação, o que colaborou para o delineamento de algumas representações deste tipo de análise. Destaca-se que a análise de conteúdo não é tarefa fácil; além da participação do pesquisador em todo o processo, buscou-se a compreensão e familiaridade com os fatos, o que favoreceu a investigação e a consulta a estudos já realizados, especialmente na área da educação, sendo que a quantidade de situações abordadas é fundamental para o estudo.
Delineamento e análise inicial da tarefa
A tarefa Modelando Sólidos Geométricos teve a finalidade de fazer com que os estudantes, por meio da manipulação de materiais concretos e tecnológicos, construíssem os sólidos, visualizassem suas formas, características e propriedades. No primeiro encontro, com duas aulas, foi realizada uma análise do conhecimento prévio e cotidiano dos alunos sobre os sólidos, discutindo-se conceitos e suas características tridimensionais.
A intenção da tutora foi explorar a teoria a partir de construções realizadas em sala de aula com lápis e papel e, posteriormente, com o programa, permitindo que os estudantes explorassem “situações-problema” e fizessem “conjecturas sobre o conteúdo” que estavam estudando (Silva, 2011, p. 13). Em seguida, os estudantes foram convidados a responder a uma tarefa impressa (Figura 1), redesenhada para o estudo.
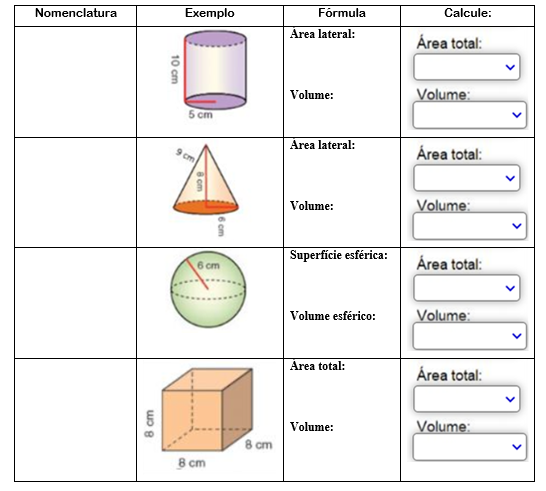
Figura 1: Primeira etapa da tarefa impressa
Considerando a atividade apresentada pela pesquisadora, podemos afirmar que cada material pedagógico possui uma proposta didática que o justifica, uma vez que os materiais concretos não podem ser apenas um experimento, uma tentativa de acerto. Mas, de acordo com Fiorentini (1995), é importante dizer que as ações em torno desses materiais devem ser pensadas, planejadas, estudadas e inseridas com seriedade e com intencionalidade.
Após a realização da primeira etapa da tarefa, passou-se para a próxima orientação, que foi a construção do protótipo virtual, utilizando sólidos geométricos para projetar os itens selecionados pela turma. O recurso tecnológico manipulado nessa tarefa foi o Tinkercad, devido a isso, foi reservada uma aula de explanação sobre o acesso ao site do programa, o uso das principais ferramentas e figuras geométricas disponíveis.
Nesse momento a turma foi dividida em grupos, em cada um, tinha pelo menos um notebook para a execução da tarefa. O que permitiu à professora observar a interação do estudante frente a uma plataforma de animação gráfica 3D, com o objetivo de aprendizagem elaborado para o estudo dos sólidos geométricos (Figura 2). A partir daí cada grupo se ocupou em fazer a construção dos sólidos e do preenchimento das fichas.

Figura 2: Realização da tarefa
Fonte: Acervo da pesquisadora.
Toda a estratégia que o programa apresentou valorizou ainda mais a concepção da professora sobre o trabalho com as tecnologias digitais nas aulas de matemática. Esse fato pode ser verificado nos argumentos dos estudantes. Para preservar a identidade dos estudantes, foram utilizadas apenas as iniciais de seus nomes nas citações.
Dá para explorar muita coisa, né? E fazer várias construções em blocos, onde você arrasta e programa do jeito que você quiser... Consegui ver rapidamente uma variedade valores para volume e área lateral do sólido, não precisei fazer outras construções no caderno, apenas simulei alguns valores em minha própria planificação (Estudante AC).
O que eu mais gostei foi poder criar objetos do meu dia-dia no computador e ao mesmo tempo estudar o assunto. E o mais legal é que pode utilizar o programa na aula de matemática. Vou estudar em minha casa essa tarefa, basta treinar que dá para fazer vários outros projetos e aprender mais (Estudante ME).
Tanto o estudante AC quanto a estudante ME perceberam as vantagens do programa utilizado na tarefa, apontando benefícios significativos para a aprendizagem, pois ressaltam o dinamismo e a animação que o software oferece, estimulando o estudante a ter curiosidade para investigar, explorar cada ponto da atividade e discutir com o professor e colegas de turma suas dúvidas e contestações referentes ao que foi encontrado. Acredita-se que “trocar ideias, compartilhar as soluções encontradas para um problema proposto, expor o raciocínio, são ações que constituem o fazer matemática” (Malheiros, 2008, p. 27).
Por isso, reforça-se a importância de diversificados padrões de ensino no ambiente de aprendizagem, com vistas a proporcionar mais informações sobre os conteúdos estudados durante as aulas. Além disso, Alro e Skovsmose (2006) destacam que tais espaços precisam apresentar condições necessárias para favorecer o aprendizado do estudante.
Outro fator que chamou a atenção nessa prática foi a organização e a preocupação com o ambiente de aprendizagem, considerando importante o tipo de tarefa a ser trabalhada com o programa. Sendo assim, a possibilidade de arrastar permite que os alunos construam a “sua aprendizagem, através da aquisição de conhecimentos e redescobertas de princípios” (Mendes, 2009, p. 110).
Como sabemos, os sólidos geométricos foram construídos pelos estudantes, que demonstraram facilidades para desenvolver suas respectivas edificações, os quais, segundo Franco (2013), são chamados de nativos digitais por apresentarem familiaridade com o uso de computadores, jogos e videogames conectados ao ciberespaço. Além disso, são capazes de pesquisar informações e processar o recebimento de tudo isso com rapidez, pois gostam de realizar inúmeras atividades ao mesmo tempo.
Os resultados foram surpreendentes, pois a maioria dos estudantes, aproximadamente 75%, além de fazer a representação gráfica dos sólidos, ainda construiu protótipos com as formas geométricas estudadas (Figura 3), colocando em prática a criatividade e a imaginação.
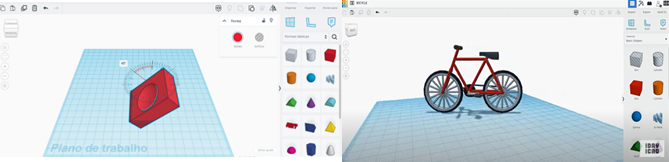
Figura 3: Protótipo objeto de estudo
Fonte: Acervo da pesquisadora.
De maneira genuína, alguns estudantes fizeram construções simples com figuras geométricas triviais; no entanto, outros, que se identificaram pelo design 3D, conseguiram criar estruturas mais elaboradas, incorporando às suas criações objetos pessoais do cotidiano. Para Resnick (2020), esse é o momento em que o aprendiz dá vazão ao processo de experimentação e vivência prática, proporcionando a validação de suas possibilidades criativas e a oportunidade de realizar ajustes em um processo de melhoria e desenvolvimento contínuo.
Os estudantes demonstraram grande interesse em desenvolver as edificações completas, verificando propriedades e nomenclaturas geométricas. Para a proposta, a professora sugeriu meios para que os estudantes investigassem o assunto abordado, tirando suas próprias conclusões. Esses resultados foram, posteriormente, discutidos com a turma, de modo que todos chegassem a um produto final sobre as descobertas desenvolvidas com o recurso.
Análise dos dados à luz dos critérios de idoneidade didática
A tarefa apresentada no estudo contempla inicialmente os indicadores do desenho de tarefas /idoneidade mediacional, considerando que são utilizados materiais manipulativos e informáticos que permitem introduzir boas situações, linguagens, procedimentos e argumentações adaptados ao significado pretendido. Logo, de acordo com Pochulu, Font e Rodríguez (2013), o estudo apoia-se na concepção de tarefas concebidas como contextos e situações diversificadas de sequências pensadas e planejadas pelo professor com o intuito de colaborar para uma adequada aprendizagem dos estudantes.
Além disso, o depoimento de outros estudantes, comprovam na tarefa destacada os indicadores referentes aos critérios interacionais e emocionais:
Muito legal essa tarefa, dá vontade de ficar manipulando a imagem o tempo todo, até consegui chegar no tamanho certo do sólido que foi pedido na tarefa. Primeiro eu calculei as medidas dos sólidos geométricos na atividade e depois passei para o programa, o que surgiram algumas dúvidas e questionamentos sobre o objeto que iria adotar para finalização da atividade. Mas a professora o tempo todo fazia comparações com outros objetos, me ajudando a perceber aquele que mais se adequava a proposta (Estudante MP).
Gostei de todas as etapas da tarefa, achei bem diferente das outras que fiz ultimamente. Em relação ao nível de dificuldade da tarefa, eu achei no começo um pouco confusa, mas, durante a aula a professora foi tirando as dúvidas de como usar o programa e também alguns colegas da turma que aprenderam mais rápido me ajudaram na atividade (Estudante BF).
Quando a estudante BF menciona “Gostei de todas as etapas da tarefa”, foi possível constatar que a prática foi contemplada pelos indicadores relacionados à afetividade, promovendo a compreensão da aplicabilidade da matemática, assim como o interesse e o comprometimento na busca de uma solução para o problema. Isso também propiciou a interação do grupo em sala de aula, a fim de lidar com as dificuldades, viabilizando, assim, a troca de conhecimentos e aprendizagens.
Percebemos ainda, a partir dos estudos de Gusmão e Font (2020), indicadores do desenho de tarefas/idoneidade cognitiva verificados nos resultados gráficos das respostas apresentadas no formulário digital que se referem a indicadores que incentivam o uso de estratégias de resolução diferentes, criativas e originais, partindo dos conhecimentos prévios dos estudantes e levando-os a desenvolver diferentes competências cognitivas.
Vejamos, assim, o resultado gráfico das respostas (Figura 4) apresentadas pelos estudantes no formulário online:
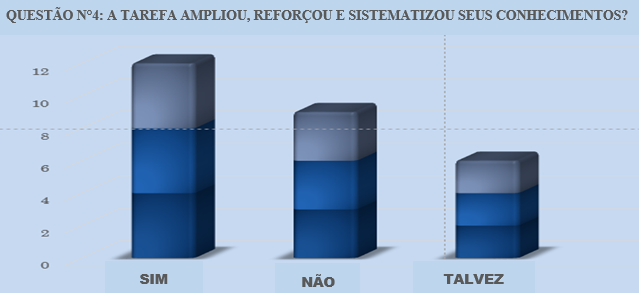
Figura 4: Recorte do formulário análise gráfica
No que se refere à ampliação, reforço e sistematização do conhecimento, verificou-se que doze dos estudantes responderam que a tarefa com o programa colaborou para o aprendizado da disciplina; porém, a pesquisa aponta que nove participantes do estudo alegaram não ter assimilado adequadamente o conteúdo durante a aula, apresentando dificuldades para manusear o programa. Também, um grupo de seis estudantes se manteve neutro quanto ao feedback da proposta de estudo.
Contudo, mesmo com essa pequena discordância de opiniões, todos os estudantes concordaram, ao final da tarefa, com a importância de diversificar as práticas desenvolvidas nas aulas de matemática. Daí, segundo Gusmão (2016), a relevância de o professor observar atentamente as tarefas que escolhe para seus alunos e propor que estes desenhem ou redesenhem tarefas interessantes, autênticas, desafiadoras e diversificadas.
Direcionando a análise gráfica para o formato dos percentuais das respostas dadas ao questionário, observou-se, em outra resposta do formulário, que a tarefa aplicada apresenta características dos indicadores do desenho de tarefas/idoneidade epistêmica, pois utiliza uma linguagem clara e adequada ao nível de ensino, empregando, de acordo com Gusmão e Font (2020), diferentes linguagens e formas de expressão matemática, seja ela verbal, gráfica, simbólica ou pictórica.
Nesse contexto, evidenciou-se ainda, nessa tarefa, a promoção dos indicadores relacionados ao levantamento de hipóteses e à abertura do pensamento reversível, flexível e descentrado (Figura 5), estimulando o uso de processos de argumentação e justificativas.
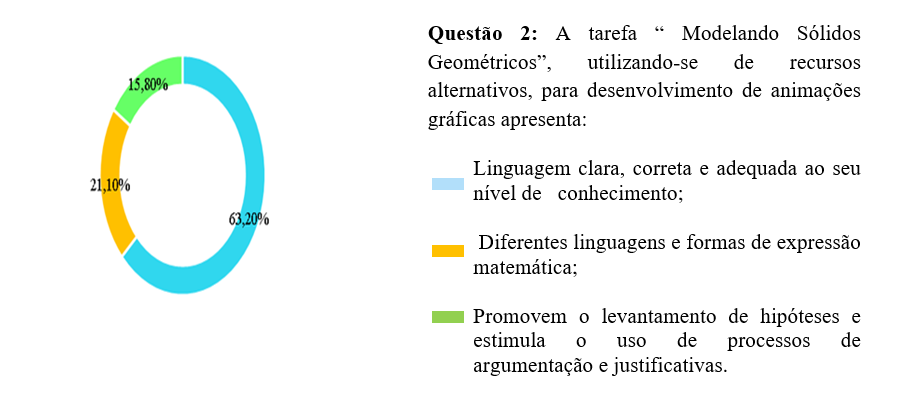
Figura 5: Análise gráfica dos percentuais
O resultado que liderou essa parte do formulário foi a linguagem clara, correta e adequada ao nível de conhecimento dos estudantes, com 63,2% dos resultados. Muitos alunos concordaram com a clareza da tarefa e reconheceram seus benefícios para a aprendizagem. Por outro lado, verificou-se, nessa mesma questão, que 21,1% dos alunos consideraram diferentes linguagens e formas de expressão matemática na tarefa, sendo que 15,8% perceberam o levantamento de hipóteses e o estímulo à argumentação e justificativas durante a prática.
Desse modo, constatou-se que a tarefa induziu uma linguagem matemática verbal de forma clara e compassada, colaborando para a aproximação dos discentes às noções pretendidas do conteúdo e utilizando a exploração para promover situações em que os alunos tivessem que construir hipóteses de forma espontânea. Ou seja, dando-lhes autonomia para responder, pois, ao mesmo tempo em que promovem a aprendizagem, as tarefas “auxiliam o professor a perceber o alcance de suas ações no desenvolvimento da cognição e metacognição” (Gusmão, 2016, p. 185).
A autora ainda aponta que a maneira como uma tarefa é constituída é muito importante para o envolvimento dos estudantes, precisando trazer meios que estimulem seu interesse. Nesse sentido, a possibilidade de associar aspectos lúdicos a materiais concretos e tecnológicos favoreceu a exploração de conhecimentos conexos ao estudo da Geometria Espacial. Esses elementos, relacionados ao conceito das formas geométricas e suas relações com a realidade, demonstraram um alto grau nos indicadores do desenho de tarefas/idoneidade ecológica, pois, além de o conteúdo fazer parte do currículo escolar, apresenta elevada relevância no cotidiano dos participantes, estando presente em seu entorno social.
Também em relação aos indicadores de idoneidade ecológica, pôde-se destacar, nas respostas dos participantes ao questionário, o indicador de que “o conteúdo da tarefa é útil para a sua vida social e laboral e busca articulação entre diferentes conteúdos da matemática e entre áreas de conhecimento”. Deste modo, um dos relatos mais reveladores foi o dos estudantes, ao afirmarem que:
A tarefa modelando sólidos geométricos no programa 3D achei bem interessante, porque eu quero ser arquiteta, e isso reforçou ainda mais a minha vontade por essa profissão, sem falar que também pode me ajudar no estudo de outras disciplinas (Estudante AJ).
Gostei tanto que pedi para a professora fazer mais edificações com o app e quero usar em casa também para outras atividades da escola.... Como por exemplo, a maquete que o professor de Biologia pediu para fazer, posso montar aqui e compartilhar no datashow com a minha turma no dia da apresentação, assim, não vou precisar usar materiais que agridem a natureza, sendo que o descarte de arquivos digitais é bem mais benéfico ao planeta! (Estudante EP).
As considerações apontadas não somente revelam a importância e aplicabilidade da tarefa no entorno social e laboral em que vivem, mas também a aprendizagem adquirida por meio dela. De acordo com Alves (2015), atividades divertidas e dinâmicas podem engajar públicos e faixas etárias diferentes. Para esse autor, o engajamento está diretamente ligado à relevância dos conteúdos, às pessoas e à forma como a aprendizagem é motivada.
Analisando sob uma perspectiva diferente, percebemos que 14% da turma, o que corresponde aproximadamente a quatro estudantes, optaram por outros aplicativos (Figura 6) e não realizaram a tarefa pelo app sugerido, considerando que tinham mais afinidade com o Minecraft e o Education Paint 3D.
Figura 6: Print da interface dos programas
Fonte: Acervo da pesquisadora.
Isso evidencia que os estudantes conseguem atender às novas demandas exigidas pelo contexto educacional, visto que seu interesse é despertado a partir de suas próprias vivências cotidianas. Além disso, para Mendes (2020), o Minecraft Education tem sido utilizado como estratégia para o ensino de diversos componentes curriculares, como Matemática, Ciências e Geografia. Com base nesses dados, percebemos que os estudantes possuem conhecimentos de outros recursos digitais, que podem auxiliá-los em suas aprendizagens, devido à capacidade de brincar e aprender, dando vazão ao processo de experimentação e vivência prática, promovendo, segundo Resnick (2020), a validação de suas hipóteses criativas, com a chance de realizar ajustes em um processo de melhoria e desenvolvimento contínuo.
Considerações finais
Este estudo buscou fomentar reflexões sobre a produção do conhecimento matemático a partir das contribuições e desafios identificados durante a utilização de tarefas matemáticas desenhadas para uso em uma plataforma de animação gráfica 3D, com base nos critérios de idoneidade didática. A proposta de ensino contemplou práticas em que articulamos ações de visualização, manipulação e experimentação, buscando a compreensão dos assuntos abordados. Teve-se o entendimento de que uma das contribuições dessa proposta foi a possibilidade de o professor proporcionar um espaço na aula para a discussão e apreensão do conhecimento pelo aluno.
Analisando as etapas da tarefa proposta, tendo como referência as apresentações e discussões observadas durante as aulas, percebeu-se que a metodologia adotada apresentou benefícios não apenas para a disciplina de Matemática, mas também para as demais áreas do conhecimento, pois estimular a exploração nas aulas é buscar princípios que ficam registrados nos modos e procedimentos dos estudantes e que muitas vezes não são considerados fatores avaliativos da escola.
Tendo como referência os Indicadores dos critérios de idoneidade didática, para a análise da tarefa Modelando Sólidos Geométricos, constatou-se que a tarefa induziu uma linguagem matemática verbal de forma clara e compassada, colaborando para a aproximação dos estudantes às noções pretendidas do conteúdo, utilizando a exploração para promover situações em que os alunos construam hipóteses de forma espontânea.
Desse modo, diante de todas essas reflexões, alcançam-se os seguintes atributos:
- Compreensão e clareza do conteúdo no momento de exploração da atividade;
- Visualização nas construções gráficas e autonomia para as descobertas;
- Promoção do trabalho colaborativo entre os envolvidos na proposta, ajudando na formulação de hipóteses;
- Interação do sujeito com o plano de investigação durante o processo de busca e aprendizagem.
Referências
ALRO, Helle; SKOVSMOSE, Ole. Diálogo e aprendizagem em Educação Matemática. Belo Horizonte: Autêntica, 2006.
ALVES, Flora. Gamification - como criar experiências de aprendizagem engajadoras: um guia completo, do conceito à prática. 2ª ed. São Paulo: DVS, 2015.
ANDRÉ, Marli Eliza Dalmazo Afonso de. Ensinar a pesquisar: como e para quê? In: SILVA, Aída Maria M.; et al. (org.). Educação formal e não formal, processos formativos e saberes pedagógicos: desafios para a inclusão social. XIII ENCONTRO NACIONAL DE DIDÁTICA E PRÁTICA DE ENSINO (ENDIPE), Recife, 2006. Anais... Recife, 2006. p. 1-20.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS (ABNT). Referências: elaboração. NBR-6023. São Paulo, 2000.
BANDEIRA, Laís Michelle de Souza Araújo et al. Instrumento de avaliação do software educacional Tinkercad: uma visão fundamentada na BNCC. In: CONGRESSO BRASILEIRO DE INFORMÁTICA NA EDUCAÇÃO, 2019. Anais... p. 1.324. DOI: 10.5753/cbie.wie.2019.1324.
BARDIN, Laurence. Análise de Conteúdo. São Paulo: Edições 70, 2009.
BRASIL. Base Nacional Comum Curricular (BNCC). Brasília: MEC/Consed/Undime, 2018.
FIORENTINI, Dario. Alguns modos de ver e conceber o ensino de Matemática no Brasil. Zetetiké, Campinas, ano 3, nº 4, p. 1-36, 1995.
FONT, Vicenç; PLANAS, Nuria; GODINO, Juan Díaz. Um modelo para o estudo dos processos de ensino e aprendizagem da Matemática. Revista para o Estudo da Educação e do Desenvolvimento, v. 33, nº 1, p. 89-105, 2010. DOI: 10.1174/021037010790317243.
FRANCO, Cláudio de Paiva. Understanding digital natives' learning experiences. Revista Brasileira de Linguística Aplicada, Belo Horizonte, v. 13, nº 2, p. 643-658, 2013. Disponível em: http://dx.doi.org/10.1590/S1984-63982013005000001 . Acesso em: 25 jun. 2015.
GIL, Antônio Carlos. Métodos e técnicas de pesquisa social. 6ª ed. São Paulo: Atlas, 2008.
GODINO, Juan Díaz et al. Componentes e indicadores de idoneidade de programas de formação de professores em Educação Matemática. Revemat: Revista Eletrônica de Educação Matemática, Florianópolis, v. 8, nº 1, p. 46-74, 2013.
GODINO, Juan Díaz et al. Um olhar da didática francesa a partir da abordagem ontossemiótica da cognição e da instrução matemática. Revista América Latina na Pesquisa em Matemática Educacional, v. 9, nº 1, p. 117-150, 2006.
GUSMÃO, Tânia Cristina Rocha Silva. Desenho de tarefas para o desenvolvimento da cognição e metacognição matemática. In: NEVES, Anderson Souza (org.). Ensino e didática das Ciências. Salvador: Edufba, 2016. p. 183-193. (Coleção Ensino, Filosofia e História das Ciências).
GUSMÃO, Tânia Cristina Rocha Silva; FONT, Vicenç. Ciclo de estudo e desenho de tarefas. Educação Matemática Pesquisa, São Paulo, v. 22, nº 3, p. 666-697, 2020.
MALHEIROS, Ana Paula dos Santos. Educação Matemática online: a elaboração de projetos de modelagem. 2008. 187f. Tese (Doutorado em Educação Matemática) – Instituto de Geociências e Ciências Exatas, Universidade Estadual Paulista, Rio Claro, 2008.
MENDES, Iran Abreu. Investigação histórica no ensino da Matemática. Rio de Janeiro: Ciência Moderna, 2009.
MENDES, Luiz Otavio Rodrigues; MULATI, Janaina; GONZALES JOLANDEK, Emilly. Apropriação de conteúdos basilares da Educação na utilização do Minecraft Education: a percepção de alunos dos anos finais do Ensino Fundamental. Revista Sergipana de Matemática e Educação Matemática, São Cristóvão, v. 5, nº 1, p. 290-309, 2020.
MORAN, José. Mudando a educação com metodologias ativas. In: SOUZA, Carlos Alberto de; MORALES, Ofélia Elisa Torres (org.). Convergências midiáticas, educação e cidadania: aproximações jovens. Ponta Grossa: UEPG/Proex, 2015. v. 2, p. 15-33. (Coleção Mídias Contemporâneas).
MOREIRA, Marco Antônio. Teorias da Aprendizagem Significativa. Porto Alegre: UFRGS, 2016. Disponível em: http://moreira.if.ufrgs.br/Subsidios6.pdf . Acesso em: 15 maio 2023.
MUNIZ, Cristiano Alberto. Brincar e jogar: enlaces teóricos e metodológicos no campo da Educação Matemática. Belo Horizonte: Autêntica, 2010.
NOVAES, Vinicius Tavares. Animações de Eletrostática para Educação de Jovens e Adultos. 2020. Dissertação (Mestrado) - Universidade Federal de Rondônia, Rolim de Moura, 2020. Disponível em: https://www.ri.unir.br/jspui/bitstream/123456789/2958/1/VIN%C3%8DCIUS%20TAVARES%20NOVAES.pdf .
NUNES, Mirian Aparecida Meliani et al. Relatos da informação nas redes sociais digitais: caminhos alternativos da produção e distribuição de notícias. In: CONGRESSO BRASILEIRO DE CIÊNCIAS DA COMUNICAÇÃO, 41., 2018, Joinville. Anais... São Paulo: Intercom, 2018.
POCHULU, Marcel; FONT, Vicenç; RODRIGUEZ, Mabel. Critérios de diseño de tareas para favorecer el análisis didáctico em la formación de profesores. In: ACTAS DEL CIBEM, 7., 2013, Montevideo. Anais... Montevidéu: Fisem, 2013.
RESNICK, Mitchel. Aprendizagem criativa: por uma educação mais expressiva, mão na massa e relevante para todos. Porto Alegre: Penso, 2020.
SILVA, Ângela Carrancho da. Educação e tecnologia: entre o discurso e a prática. Ensaio: Avaliação e Políticas Públicas em Educação, Rio de Janeiro, v. 19, nº 72, p. 527-554, jul./set. 2011.
TOSCANI, Rafael et al. Produção de animações computadorizadas em Flash para o ensino básico de Geociências. Terra e Didatica, Campinas, v. 13, nº 3, p. 271-278, 2018. DOI: 10.20396/td.v13i3.8651221. Disponível em: https://periodicos.sbu.unicamp.br/ojs/index.php/td/article/view/8651221 . Acesso em: 10 maio 2024.
TRIVIÑOS, Augusto Nibaldo Silva. Introdução à pesquisa em ciências sociais: a pesquisa qualitativa em educação. São Paulo: Atlas, 1987.
Publicado em 29 de outubro de 2025
Como citar este artigo (ABNT)
BATISTA, Gabriele Silva Carneiro; ARAÚJO, Marisa da Silva. Aprendizagem e animação 3D no Tinkercad: um estudo sobre sólidos geométricos à luz dos critérios de idoneidade didática. Revista Educação Pùblica, Rio de Janeiro, v. 25, nº 41, 29 de outubro de 2025. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/25/41/aprendizagem-e-animacao-3d-no-tinkercad-um-estudo-sobre-solidos-geometricos-a-luz-dos-criterios-de-idoneidade-didatica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

