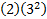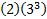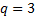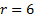Construindo uma sequência de recorrência: uma possibilidade para o estudo das progressões geométricas e aritméticas na Educação Básica

O conhecimento matemático sobre progressões geométricas e aritméticas é fundamental para a formação dos estudantes da Educação Básica, já que o desenvolvimento do pensamento algébrico requer a identificação de padrões em sequências numéricas e a investigação de generalizações. A relevância dessa temática de observação de padrões também é evidenciada na competência 5 da Base Nacional Comum Curricular (BNCC):

Investigar e estabelecer conjecturas a respeito de diferentes conceitos e propriedades matemáticas, empregando estratégias e recursos, como observação de padrões, experimentações e diferentes tecnologias, identificando a necessidade, ou não, de uma demonstração cada vez mais formal na validação das referidas conjecturas (Brasil, 2018, p. 531).

As progressões aritméticas (P.A.) e geométricas (P.G.) também estão relacionadas ao estudo de funções: a P.A. é associada às funções afins, e a P.G., às funções exponenciais. Essas conexões aparecem nas habilidades EM13MAT507 e EM13MAT508 da BNCC (Brasil, 2018, p. 541).

Autores como Paiva (2010) e Rocha (2019) trouxeram contribuições significativas sobre as progressões aritmético-geométricas e geométrico-aritméticas, aprofundando o estudo dessas sequências e explorando suas combinações. O objetivo deste artigo é definir uma sequência de recorrência que utilize as razões de uma P.A. e de uma P.G. dadas, diferenciando-se das sequências já tratadas pelos autores mencionados. Além disso, será apresentada uma abordagem didática para explorar esse tema no ensino de Matemática da Educação Básica.

Definição da sequência de recorrência

Para a construção da nossa sequência, utilizaremos uma P.A. cujo enésimo termo é dado pela expressão 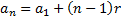, com 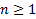, e uma P.G. cujo enésimo termo é dado por 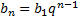, com 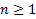. Aqui, 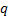 e 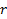 são números reais positivos.

Assim, definiremos uma sequência de números reais cujo o enésimo termo é dado por:

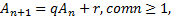
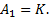
Essa sequência caracteriza-se como uma relação de recorrência linear de primeira ordem: a) linear, pois o termo 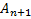 é uma combinação linear de um ou mais termos anteriores; b) de primeira ordem, pois 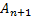 depende de um único termo anterior; c) não homogênea, já que .

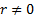A fórmula posicional para o termo 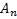 pode ser obtida verificando-se os primeiros termos:

,

,

,

…

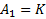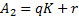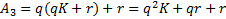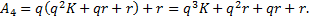
Observa-se que:

.

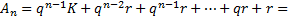
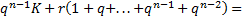
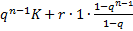Ou seja:

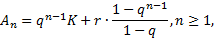
Trata-se da chamada solução da relação de recorrência, isto é, sua fórmula posicional.

Com essa fórmula, verifica-se que, para 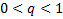, o limite de 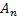 quando 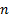 tende a infinito é:

,

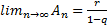pois, nesse caso, .

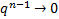Logo, a sequência converge quando 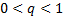. Porém sua soma infinita não irá convergir, pois, se o termo geral de uma sequência não tende a zero, então a sua série diverge, que é o caso aqui.

Ainda assim, é possível obter uma fórmula para a soma finita dessa sequência, como demonstrado a seguir.

Soma finita

Sabe-se que .

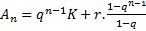Ou seja:

.

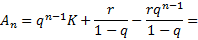
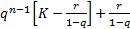Somando os 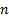 primeiros termos, tem-se:

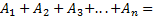
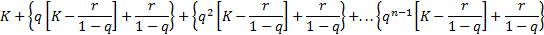
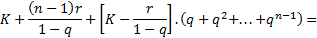
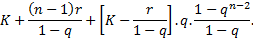
Diferença com relação a outras P.A.G. e P.G.A.

Conforme mencionado, outros modelos de P.A.G. (progressão aritmético-geométrica) e P.G.A. (progressão geométrico-aritmética) já foram considerados. Um modelo construído foi o de Paiva. Segundo o autor, uma P.A.G. é uma sequência (an) cujo termo geral é dado por:

,

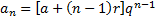sendo 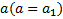, 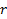e 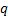constantes não nulas e .

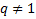Nesse modelo, para a obtenção do seu termo geral, a razão 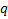 da P.G. é multiplicada pelo termo geral da P.A. interna ao colchete. O autor ainda deduz a fórmula da soma finita da P.A.G. e prova que, se 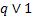, então a sua soma infinita converge.

No mesmo artigo, é definida a P.G.A. cujo termo geral é:

.

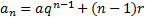Nessa sequência, a razão 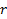 da P.A. é somada ao termo geral da P.G. 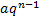. O autor deduz a fórmula da soma finita dela. Porém, no artigo, não é dito se a soma infinita converge ou diverge.

Comparando essas sequências com a que foi proposta neste artigo, o termo geral 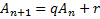 é distinto dos dois modelos descritos acima. Aqui o termo geral é, na verdade, uma fórmula de recorrência.

Possibilidade de utilização na Educação Básica: sequência didática

Segundo Monteiro, Castilho e Souza (2019), uma sequência didática é um conjunto de atividades que estabelece um ambiente propício para a aprendizagem, especialmente em Matemática. Trata-se de atividades interconectadas e cuidadosamente planejadas para ensinar determinado conteúdo de forma progressiva, organizadas conforme os objetivos definidos pelo professor, visando ao alcance da aprendizagem esperada pelos alunos.

A sequência didática pode ser planejada para execução em várias aulas, sendo importante considerar o tempo de cada etapa, os objetivos de aprendizagem, a avaliação formativa, os exercícios, os textos, o material didático e os horários. Diferentemente do plano de aula, que geralmente se refere a um único encontro, a sequência didática constitui um conjunto de planos de aulas logicamente interligados, detalhando execução, tempo, materiais, quantidade de alunos e demais fatores presentes nas aulas, com o objetivo do ensino de determinado(s) conteúdo(s).

Para a utilização da sequência de recorrência proposta neste artigo, sugerimos uma sequência didática com, no mínimo, três aulas. A seguir, descrevemos as principais características dessas aulas, que podem ser realizadas com turmas de até 40 alunos, cada uma com duração aproximada de 40 minutos. Essas atividades são indicadas para estudantes do Ensino Médio, com avaliação baseada na observação da realização das tarefas.

Aula 1 - progressões aritméticas

O objetivo principal desta aula é revisar com os estudantes a fórmula do termo geral de uma P.A. Inicie orientando-os a observar a seguinte P.A.: 3, 5, 7, 9, 11, 13, 15, 17 etc. Explique que os termos consecutivos diferem por um valor constante, chamado de razão. Neste exemplo,  a razão ( 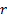) é igual a 2.

Em seguida, peça aos alunos que completem uma tabela como a seguinte, evidenciando quanto está sendo somado da razão em cada termo:

Tabela 1: Sequência para os alunos completarem de uma P.A.

Termos da P.A.	Primeiro termo	Segundo termo	Terceiro termo	Quarto termo
	3	3+2	3+(2 2)	3+(3×2)

Conduza a discussão para concluir que o enésimo termo dessa P.A. pode ser escrito como:

.

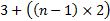Dessa forma, observe que, no caso geral, em que o primeiro termo seja 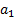 e a razão 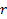, o enésimo termo 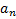 será dado por:

.

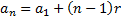Se houver tempo, forneça uma outra P.A., como, por exemplo, 1, 5, 9, 13, … e peça aos alunos para encontrarem o termo geral dessa sequência, a partir do preenchimento de uma tabela como a realizada anteriormente.

Aula 2 - progressões geométricas

Nesta aula, o objetivo principal é revisar a fórmula do termo geral de uma P.G. inicie apresentando a seguinte P.G.: 2, 6, 18, 54, 162 etc. Explique que a divisão entre dois termos consecutivos resulta em um valor constante, chamado razão. Nesse exemplo a razão ( 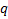) é igual a 3.

Em seguida, peça aos alunos que completem uma tabela como a do exemplo que segue, deixando evidente quanto está sendo multiplicado da razão em cada termo.

Tabela 2: Sequência para os alunos completarem de uma P.G.

Termos da P.G.	Primeiro Termo	Segundo Termo	Terceiro Termo	Quarto termo
	2	(2)(3)	(2)(3)(3) =	(2)(3)(3)(3) =

Conduza a discussão para concluir que o enésimo termo dessa P.G. pode ser escrito como 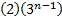. Dessa forma, observe que, no caso geral, em que o primeiro termo seja 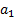 e a razão 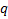, o enésimo termo 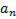 será dado por: .

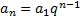Se houver tempo, forneça uma outra P.G., como, por exemplo,  4, 8, 16, ... e peça aos alunos para encontrarem o termo geral dessa sequência, preenchendo uma tabela similar à anterior.

Aula 3 – Construindo a sequência de recorrência

O objetivo desta aula é construir a sequência de recorrência 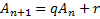na qual 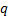 é a razão de uma progressão geométrica dada e 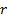 é a razão de uma progressão aritmética inicialmente fornecida. No primeiro momento, o professor deve pedir para os estudantes criarem uma progressão aritmética e uma progressão geométrica e colocarem seus termos em uma tabela como a do exemplo a seguir.

Tabela 3: Construindo uma sequência de recorrência

	Primeiro termo	Segundo termo	Terceiro termo	Quarto termo	Razão
P.G.	5	15	45	135
P. A.	4	10	16	22

Em seguida, os alunos devem preencher uma tabela (como a que segue) com as informações da razão da P.G. e P.A. da tabela anterior. Além disso, eles devem escolher um número para ser o primeiro termo da sequência de recorrência. Nesse exemplo, escolhemos o número 10.

Tabela 4: Construindo uma tabela com P.G. e P.A.

	Primeiro termo	Segundo termo	Terceiro termo	Quarto termo
Sequência de recorrência	10	3×10+6 =36	3×36+6 = 114	3×114+6=348

Por fim, peça que os alunos encontrem o sexto termo e o décimo termo dessa sequência, bem como seu enésimo termo.

Conclusão

O presente artigo propôs uma maneira de abordar as progressões aritméticas e geométricas no ensino de Matemática da Educação Básica utilizando uma sequência de recorrência construída com base nas razões de uma P.A. e de uma P.G. dadas. Essa abordagem pode contribuir para uma compreensão mais ampla e integrada desses conteúdos.

Também foi apresentada uma sequência didática composta por três aulas de 40 minutos cujo objetivo foi explorar as possibilidades pedagógicas do tema das sequências de recorrência a partir das P.A. e P.G. Essas atividades foram desenvolvidas para alunos do Ensino Médio, com avaliação baseada na observação e na realização das tarefas propostas.

Outras atividades relacionadas à soma finita das sequências de recorrência e às diferenças entre a sequência proposta neste artigo e as P.A.G. e P.G.A. também podem ser exploradas em trabalhos futuros, ampliando as aplicações e a pesquisa sobre o tema.

Referências

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília: MEC, 2018. Disponível em: http://bncc_ei_ef_110518_versaofinal_site.pdf. Acesso em: 21 nov. 2023.

MONTEIRO, J. C.; CASTILHO, W. S.; SOUZA, W. A. Sequência didática como instrumento de promoção da aprendizagem significativa. Revista Eletrônica DECT, Vitória, v. 9, nº 1, 2019.

PAIVA, R. E. B. Progressões aritmético-geométricas e geométrico-aritméticas. Revista do Professor de Matemática, v. 73, p. 47-49, 2010.

ROCHA, R. A. Progressões geométrico-aritméticas e aritmético-geométricas generalizadas. Revista do Professor de Matemática, v. 7, p. 36-44, 2019.