Regiões poligonais triangulares: uma investigação com dobraduras no Ensino Fundamental
Gilmar Steigleder Paschoal
Doutorando em Ensino de Ciências e Matemática (UFN/RS), professor de Matemática na rede estadual do Rio Grande do Sul
Anne Desconsi Hasselmann Bettin
Doutoranda em Ensino de Ciências e Matemática (UFN/RS)
José Carlos Pinto Leivas
Docente no Programa de Pós-Graduação em Ensino de Ciências e Matemática da UFN/RS
Este trabalho aborda uma investigação com dobraduras em aula síncrona pelo Google Meet no estudo de triângulos, mais especificamente na classificação das regiões poligonais triangulares quanto aos lados. As atividades investigativas foram aplicadas em uma escola pública do Rio Grande do Sul visando a um ensino colaborativo.
Atualmente, percebe-se a tendência dos profissionais da Educação na busca e manipulação correta das ferramentas digitais, almejando aproveitar o potencial educacional delas. Com esse intento, surge a questão: como adaptar o uso de materiais manipuláveis para desenvolver motricidade e habilidades como a imaginação e a percepção visual podem ser realizadas em ensino remoto?
Para responder a essa pergunta, foi elaborada uma investigação com dobraduras, a qual foi aplicada no 7º ano do Ensino Fundamental com o objetivo de investigar de que forma as dobraduras auxiliam no ensino-aprendizagem de formas geométricas.
Os resultados da pesquisa evidenciam que o uso de dobraduras no ensino de Matemática pode auxiliar no processo de ensino-aprendizagem de conceitos geométricos mesmo em aulas síncronas, desenvolvendo nos alunos habilidades de visualização, imaginação, criatividade, atenção, memorização, motricidade e pensamento geométrico, além de ser um material didático de baixo custo.
Fundamentação teórica
O pensamento geométrico é muito importante na Matemática e em outras áreas do conhecimento. A Base Nacional Comum Curricular (BNCC) registra, na unidade temática Geometria para os anos finais do Ensino Fundamental, que:
a Geometria envolve o estudo de um amplo conjunto de conceitos e procedimentos necessários para resolver problemas do mundo físico e de diferentes áreas do conhecimento. Assim, nessa unidade temática, estudar posição e deslocamentos no espaço, formas e relações entre elementos de figuras planas e espaciais pode desenvolver o pensamento geométrico dos alunos. Esse pensamento é necessário para investigar propriedades, fazer conjecturas e produzir argumentos geométricos convincentes (Brasil, 2018, p. 271).
Trabalhos como o de Silva (2021) evidenciam que unir a teoria com a prática auxilia no desenvolvimento dos conceitos matemáticos, despertando o interesse pela Matemática. Em seu trabalho Práticas educacionais na formação inicial do pedagogo baseadas na arte de dobrar papel, foram mostradas algumas contribuições do origami para o ensino da Matemática.
Explorar propriedades geométricas por meio de dobraduras para construir formas e estabelecer relações entre os elementos de figuras planas e espaciais, além de atuar como elemento motivador no estudo de Geometria, pode ser um recurso pedagógico para o desenvolvimento do pensamento geométrico dos alunos, mesmo numa aula síncrona, com o uso de materiais manipulativos.
De acordo com Souza e Oliveira (2010, p. 2), “materiais manipuláveis são objetos desenvolvidos e/ou criados para trabalhar com conceitos matemáticos de forma que venha a facilitar a compreensão e o desenvolvimento do aluno, de modo que os estudos possam ser realizados de maneira prazerosa”.
Envolver a percepção e a manipulação de formas geométricas com o uso de dobraduras pode auxiliar na visualização, o que é apontado por Gutiérrez (1996, p. 9) como “um tipo de raciocínio baseado no uso de elementos visuais e espaciais, sejam mentais ou físicos, desenvolvidos para resolver problemas ou provar propriedades”. Leivas (2009, p. 22) afirma que a visualização é “um processo de formar imagens mentais, com a finalidade de construir e comunicar determinado conceito matemático, com vistas a auxiliar na resolução de problemas analíticos ou geométricos”.
As imagens mentais formadas pelas dobraduras comunicam um conceito matemático muitas vezes não perceptível num único tipo de registro semiótico. A visualização em Geometria pode ser estimulada por meio de investigações geométricas, pois
as investigações geométricas contribuem para perceber aspectos essenciais da atividade matemática, tais como a formulação e testes de conjecturas e a procura e demonstração de generalizações. A exploração de diferentes tipos de investigação geométrica pode também contribuir para concretizar a relação entre situações matemáticas, desenvolver capacidades como a visualização espacial e o uso de diferentes formas de representação, evidenciar conexões matemáticas e ilustrar aspectos interessantes da história e evolução da Matemática (Ponte, 2006, p. 71).
Na construção da dobradura, o estudante pode verificar propriedades, elementos visuais das figuras geométricas já estudadas, estando em conformidade com a BNCC (2018, p. 272), que afirma que,
no Ensino Fundamental – anos finais, o ensino de Geometria precisa ser visto como consolidação e ampliação das aprendizagens realizadas. Nessa etapa, devem ser enfatizadas também as tarefas que analisam e produzem transformações e ampliações/reduções de figuras geométricas planas, identificando seus elementos variantes e invariantes, de modo a desenvolver os conceitos de congruência e semelhança.
Assim, a investigação geométrica por meio de dobraduras permite aos alunos visualizar outras regiões geométricas planas ou espaciais também por meio de comparação.
Procedimentos metodológicos
O lócus de nossa investigação científica foi uma escola pública de Educação Básica situada no centro do Estado do Rio Grande do Sul. A escola possui aproximadamente 1.200 alunos na Educação Infantil, nos anos iniciais e finais do Ensino Fundamental, no Ensino Médio e no curso técnico em Administração – todos funcionando nos três turnos de ensino.
A investigação com dobraduras no estudo de triângulos ocorreu em uma aula síncrona pelo Google Meet e objetivou investigar de que forma as dobraduras auxiliam no ensino-aprendizagem de formas geométricas.
Conforme Frota (2005, p. 2-3),
práticas investigativas introduzidas na sala de aula de Matemática parecem ser cruciais para o desenvolvimento de uma postura especulativa em Matemática, podendo gerar um deslocamento do foco da aula, do professor para o aluno, no sentido de uma aula mais colaborativa. Atividades de investigação podem conformar uma concepção de Matemática como algo dinâmico, do conhecimento matemático como em construção, através do desenvolvimento de ideias e processos, constituintes do pensar e fazer matemáticos.
A atividade foi realizada em duas turmas de 7º ano do Ensino Fundamental, cada uma constituída de 30 alunos, com a participação, porém, de somente a metade do efetivo.
Antecedendo a aplicação da atividade investigativa, o professor titular da turma solicitou aos alunos que, para a aula seguinte, tivessem consigo folhas de papel ofício ou, se não conseguissem esse tipo, folhas de caderno ou até mesmo folhas de revista. Também lhes foi solicitado que tivessem régua, lápis, caneta e uma tesoura caso fosse necessário o uso desse material. Os alunos questionaram o tipo de atividade que seria proposta e o professor estimulou-os, dizendo: “não deixem de assistir à nossa próxima aula, pois tenho certeza de que gostarão muito!”. O professor ainda informou que fariam uma atividade envolvendo dobraduras no estudo de triângulos.
Para realizar a coleta dos dados, foi solicitado aos alunos que acompanhassem os procedimentos de apresentação do professor por meio das dobraduras sobre a classificação das regiões poligonais triangulares quanto aos seus lados.
Assim, a atividade proposta visou estimular habilidades de visualização, imaginação, construção e revisão de conceitos geométricos euclidianos envolvidos na dobradura e teve por objetivo o reconhecimento dos polígonos, do tipo de triângulos e sua classificação quanto aos lados.
Ao explorar as dobraduras, pretende-se trabalhar, dentre outras, habilidades como as orientadas pela BNCC (2018, p. 303):
(EF06MA18) Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e classificá-los em regulares e não regulares, tanto em suas representações no plano como em faces de poliedros.
(EF06MA19) Identificar características dos triângulos e classificá-los em relação às medidas dos lados e dos ângulos.
(EF06MA20) Identificar características dos quadriláteros, classificá-los em relação a lados e a ângulos e reconhecer a inclusão e a intersecção de classes entre eles.
Foram propostas três atividades com dobraduras. Cada uma delas com um objetivo diferente. A primeira consistia em construir uma região poligonal do triângulo equilátero (Figura 1) e teve por finalidade retomar conceitos de Geometria Euclidiana estudadas, como: ponto, reta, plano, tipo de retas, segmento, medição e comparação e construir, por meio da visualização, outros conceitos, como polígonos, regiões poligonais e definição de triângulo equilátero.

Figura 1: Passos da construção da região poligonal do triângulo equilátero
A segunda atividade visava retomar alguns conceitos de Geometria Euclidiana já estudados e construir, por meio da visualização, outros: ângulo, mediana, ponto médio de segmento e definição de triângulo isósceles. Essa atividade propõe que os alunos construam uma região poligonal do triângulo isósceles, seguindo um passo a passo conforme a Figura 2.

Figura 2: Passos da construção da região poligonal do triângulo isósceles
A atividade 3 propõe dois processos: primeiro, construir, por meio de dobradura, uma região poligonal do triângulo escaleno, visando à retomada de alguns conceitos de Geometria Euclidiana; segundo, formular, a partir da visualização, outros conceitos, como eixo de simetria e definição de triângulo escaleno. Os passos da construção podem ser visualizados na Figura 3.

Figura 3: Passos da construção da região poligonal do triângulo escaleno
É importante destacar aqui que, para a melhor avaliação do professor quanto aos resultados obtidos, ele solicitou que os alunos fossem tirando fotos das etapas das atividades que iam desenvolvendo.
Ao final da atividade investigativa, o professor apresentou aos alunos alguns vídeos que envolviam a criação de atividades com dobradura, tais como a criação de uma máscara de pandemia do tipo “coelhinho de Páscoa”. Entre outras propostas, solicitou também, como atividade complementar, que os alunos escolhessem um dos vídeos vistos, fizessem a dobradura apresentada nele e, ao concluir, enviassem ao professor uma foto da construção feita.
Resultados e discussões
A abordagem feita pelo professor, apresentando os passos da criação de dobraduras, ocorreu de forma tranquila, e os alunos acompanharam atentamente cada passo, questionando e fazendo considerações a partir do que já sabiam e do que estavam visualizando, associando os conceitos já estudados aos novos.
Apresentam-se aqui apenas alguns diálogos considerados importantes. O professor é representado por P e seus alunos por E1, E2, ..., E15.
Na primeira atividade, os alunos não souberam o nome da representação mostrada pelo professor (região triangular). Ele orientou que, nessa primeira atividade, não recortariam o papel e que, após terminarem a construção, poderiam colori-la e decorá-la como quisessem para depois postarem no Google Classroom.
Para iniciar a atividade, foi solicitado aos alunos que dobrassem ao meio a folha de papel no sentido da borda maior. Depois de dobrarem e desdobrarem, deveriam informar o que ficou marcado na linha de dobra. Muitos responderam “uma reta” e, ao lhes ser solicitado que colocassem um nome para essa reta, o estudante E7 respondeu rápido: “Em minúsculo, né, professor?”, demonstrando conhecimentos adquiridos em aulas anteriores sobre como representar a reta no papel. E o professor continuou a explicação:
P: Pegue um cantinho, marque uma seta e outra na dobra. Depois, dobre de modo que o canto que tem a seta fique sobre a reta próxima da outra seta e o canto de baixo forme um ângulo, conforme a Figura 4 (Diálogo entre o professor e os alunos, 2021).


Figura 4: Instrução inicial da dobradura
Essa etapa da construção exigiu o desenvolvimento de habilidades como atenção, concentração, motricidade e habilidades manuais para efetuar as dobras de forma correta. Nesse momento, é importante a orientação do professor para a forma como o aluno está vendo a folha, ou seja, sua percepção acerca da posição: para uns pode estar na vertical; para outros, na horizontal.
A questão era como as retas poderiam ser classificadas.
P: Concordam que formou uma nova reta? Vamos dar um nome a ela. Como vamos chamar?
E1: Reta vertical.
E12: inclinada.
E15: Chamar de i de inclinada (Diálogo entre o professor e os alunos, 2021).
P: As retas formaram um ponto aqui, vamos chamar de ponto A. Aproveitando, que tipo de retas temos?
E7: Concorrentes (Diálogo entre o professor e o aluno, 2021).
Os alunos acompanham atentamente, participando da aula, mostrando as dobras que iam fazendo e respondendo às perguntas do professor.
P: Agora, dobre a folha nesse sentido do lado (em que estão os dedos), de cima para baixo, conforme a Figura 5.
E5: Vai ficar um triângulo com pernas para baixo (Diálogo entre o professor e o aluno, 2021).


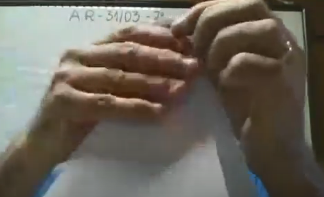
Figura 5: Passos da construção da dobradura
Percebe-se, na fala dos alunos, como “pernas para baixo”, que eles atribuem características de seres animados aos objetos matemáticos, algo que começa a ser deixado de lado para a construção de conceitos, verificação de propriedades e elementos visuais das formas geométricas estudadas. A exploração das propriedades geométricas, por meio da percepção e manipulação das dobraduras, parece dar subsídios para o desenvolvimento do pensamento geométrico do aluno.
O professor mostra aos alunos como ficou a folha dobrada, conforme a Figura 6.

Figura 6: Folha dobrada
P: Desdobrando a folha, o que vocês observam?
E7: Criou outra reta.
E9: Vamos nomeá-la de reta f e o ponto de ponto B (Diálogo entre o professor e os alunos, 2021).
Só um dos alunos não conseguiu fazer a última dobra, solicitando ajuda ao professor, que repetiu a explicação. O docente verificou, também, que um dos estudantes indicou a reta f com letra maiúscula; por isso explicou novamente como nomear o ponto, a reta e o plano. Depois, solicitou que executassem os passos 4 e 5 da Figura 1.
Após desdobrar, ficou mais uma reta, a ser nomeada de g. Então a folha é dobrada novamente para o lado de dentro para ficar com um dos lados sem dobras. A partir disso, o professor questionou os alunos sobre que região poligonal da figura geométrica está limitada pelas três linhas de dobra.
E7: Triângulo equilátero.
P: Peguem a régua e meçam. Qual a medida? (Diálogo entre o professor e o aluno, 2021).
Nesse momento, utilizaram-se instrumentos de medida como a régua, conforme BNCC (2018, p. 305) com a orientação: “(EF06MA22) é recomendado que alunos utilizem e aprendam a usar instrumentos de medida”.
E8: Para mim falta um tracinho para chegar no 24.
E7: Mais de 24cm e menos de 24,5cm.
E12: Tem todos os lados iguais, todos os lados de mesmo tamanho.
P: Esse lado como se chama?
E7: Segmento.
P: O menor polígono que nós temos é o triângulo, e como ele tem os três lados iguais ele é chamado de triângulo equilátero e, juntamente com a região interna dele, temos a região poligonal do triângulo equilátero. Façam uma arte nele depois, pode falar com a professora de Educação Artística, tirem uma foto do triângulo e outra da folha aberta com as marcações, pontos e retas.
E5: Marcar com caneta as retas (Diálogo entre o professor e os alunos, 2021)
Enfatiza-se como é importante proceder à medição e explicar o que representa o “tracinho”, estimular os alunos a pensar e falar suas percepções, pois, na aula síncrona, o professor muitas vezes não consegue visualizar com exatidão todas as medições dos alunos e sempre há uns tímidos ou aqueles que têm medo de responder.
Ao continuar as instruções para a dobradura, o professor pede que dobrem a ponta para baixo, conforme a Figura 7.

Figura 7: Dobradura da região poligonal do trapézio
P: Vamos ter uma figurinha bem legal!
E7: É um trapézio, né, professor? Ficam três triângulos (Diálogo entre o professor e o aluno, 2021).
Observa-se que os alunos conseguem estabelecer as conexões matemáticas mencionadas por Ponte (2006), de figuras geométricas já estudadas, visualizando outras formas geométricas na mesma dobradura. O professor solicitou que desdobrassem a folha e que verificassem quantos triângulos ficaram demarcados.
A maioria dos alunos respondeu que ficaram demarcados três ou quatro. Apenas o estudante E7 apresentou uma percepção muito boa da visualização de triângulos na dobradura ao responder “cinco”, pois visualizou um grande no meio e quatro dentro.
P: Do trapézio podemos dobrar uma parte e formar um...
E7: Losango.
P: E se dobrar de novo?
E5: Um triângulo (Diálogo entre o professor e os alunos, 2021).
O professor solicitou que pintassem, com cores diferentes se fosse possível, as regiões poligonais do triângulo, do losango e do trapézio. A ideia era trabalhar com figuras planas, mas um dos alunos questionou o professor:
E1: Professor, se o senhor levantar esse triângulo maior vai ficar outro triângulo, em forma de cubo, assim, não sei como é o nome (Diálogo entre o professor e o aluno, 2021).
Percebe-se aqui que não foi planejado o trabalho com a Geometria Espacial, mas durante a atividade o estudante questionou se não poderia representar outra forma geométrica (Figura 8).

Figura 8: Aluno E1 mostrando a dobradura em formato de objeto espacial
Outro estudante complementou que poderia ser uma pirâmide. Isso vem ao encontro do que Skovsmose (2008) diz sobre a aplicação desse tipo de atividade: “um cenário para investigação é aquele que convida os alunos a formular questões e a procurar explicações” (2008, p. 21), como as que ocorreram durante a aula. O professor associa e comenta a planificação da pirâmide, conteúdo a ser trabalhado conforme consta na BNCC para esse mesmo ano escolar.
Os alunos participam de forma ativa do seu processo de aprendizagem, explorando, questionando e elaborando novas conjecturas. “Quando os alunos assumem o processo de exploração e explicação, o cenário para investigação passa a constituir um novo ambiente de aprendizagem” (Skovsmose, 2008, p. 21). Dessa forma, a atividade investigativa de dobraduras no formato remoto mostrou que é eficiente para trabalhar, construir e relembrar conceitos geométricos euclidianos no 7º ano do Ensino Fundamental.
P: É uma pirâmide, mas também é chamada de tetraedro, disse o professor. Por que tetra?
E15: Porque tem quatro lados.
P: Vamos abrir ela, planificar; podemos dizer que a do meio é a base e os outros são as faces (Diálogo entre o professor e o aluno, 2021).
Para a construção desse triângulo equilátero e sua região poligonal, foram trabalhados os conceitos de reta, tipos de retas, segmentos e polígonos que podemos formar com a figura, e até mesmo um tetraedro, transcorrendo aproximadamente 30 minutos de aula.
Na atividade 2 foi construído um triângulo isósceles. O professor pegou outra folha já dobrada, que representava outro tipo de triângulo, e perguntou aos alunos qual tipo de figura ela representaria. Perguntou ainda se seria igual à outra construída antes. Um dos alunos respondeu que as medidas eram diferentes.
Então, o professor começou a construção com seus alunos (Figura 9).

Figura 9: Passo inicial para construir um triângulo isósceles por meio de dobraduras
P: Dobre o lado que sobrou da folha para cima da que está dobrada e coloque o nome de retas, depois dobre o pedacinho que falta para dentro e nomeio de reta t. Que figura formou?
E1: Outro triângulo (Diálogo entre o professor e o aluno, 2021).
O professor fez vários questionamentos para verificar o aprendizado dos alunos, como colocar um triângulo sobre o outro e verificar se são iguais; se têm a mesma medida; se os ângulos internos têm a mesma medida. Solicitou ainda que os alunos medissem a região poligonal construída.
Nessa segunda atividade, os alunos conseguiram fazer as construções e medições corretas. Assim, classificaram o triângulo quanto aos lados, chamando-o de triângulo isósceles. O professor fez novos questionamentos sobre esse triângulo construído.
P: Se dobrar fica um sobre o outro; se abrir, vão perceber que tem dois triângulos isósceles? Meçam novamente.
E15: No meu... os dois lados iguais, deram 15cm e o de baixo deu 21cm.
E7: Nem precisa medir é só ver metade do valor anterior. Essa medição ao meio (Diálogo entre o professor e os alunos, 2021).
Mais alunos confirmaram as medidas, e o aluno E7 fez um comentário interessante que possibilitou ao professor aproveitar o momento e explicar o conceito de mediana e ponto médio, conforme a Figura 10.

Figura 10: Explicação, por meio de dobraduras, do significado de ponto médio e mediana
Na terceira atividade, o objetivo era retomar alguns conceitos de Geometria Euclidiana já estudados e construir, por meio da visualização, outros conceitos como eixo de simetria, losango e definição de triângulo escaleno.
O professor iniciou mostrando um terceiro triângulo e perguntando se ele era equilátero. Os alunos logo compreenderam que ele não tinha nenhum lado igual, mas não sabiam como ele se chamava, segundo a classificação quanto aos lados. Um deles até arriscou a resposta, dizendo “irregular”; nesse momento, outro lembrou “escaleno”. Assim, prosseguiu a construção desse novo triângulo.
Foi solicitado aos alunos que pegassem outra folha e dobrassem conforme a Figura 9 e recortassem o que sobrasse. Ao desdobrarem, formou-se a representação de outra região poligonal, que todos os alunos conheciam: o quadrado. Ao dobrar novamente no vinco anterior, o professor questionou os alunos:
P: Que triângulo ficou, dobrando novamente?
E6: Equilátero ...
E11: Para mim parece isósceles.
P: Como tem ângulo de 90 graus, é conhecido como retângulo; os engenheiros usam esse ângulo para construir a casa nos quatro ângulos da casa (Diálogo entre o professor e os alunos, 2021).
O professor começa a explicar algumas aplicações dos triângulos no nosso cotidiano e onde os encontramos. Após um momento de descontração, surgido devido a um comentário de um dos alunos ao dizer que dava para fazer um avião se dobrasse de determinada forma, continuaram as dobraduras. Em determinada fase da construção, a dobradura ficou muito semelhante a uma pandorga, um losango, e o professor comentou isso com a turma.
Ao finalizar a construção, o professor questionou que tipo de triângulo foi construído, e os alunos responderam que foi um tipo diferente de triângulo cujo nome não sabem.
Após os alunos medirem os lados, o professor explicou que se pode classificar esse triângulo quanto à medida de seus lados. Como eles têm medidas diferentes, o triângulo é chamado de triângulo escaleno.
O professor dobrou uma parte do triângulo formado conforme a Figura 11 e perguntou aos alunos que tipo de triângulo era; os alunos responderam: esquadro, triângulo retângulo, escaleno, triângulo escaleno retângulo, até que um disse ‘triângulo retângulo”. O professor pediu para contornar a linha que forma o triângulo retângulo e mostrou que o interior é chamado de região poligonal do triângulo retângulo.

Figura 11: Região poligonal do triângulo retângulo formado
Como tarefa, os alunos postaram suas construções com dobraduras no Google Classroom, conforme pode ser conferido na Figura 12.

Figura 12: Resultado das três atividades do aluno E3
A produção dos alunos referente às dobraduras ajudou a desenvolver muitas habilidades, como a motricidade e a percepção espacial, auxiliando no ensino-aprendizagem de formas geométricas, como o triângulo e respectivas regiões na aula síncrona. A partir disso, foram possíveis a construção e a retomada de conceitos geométricos por meio da visualização das dobraduras.
Com essas atividades, o conhecimento deixou de ser estático e se ampliou, incentivando a imaginação e desenvolvendo a percepção. A intenção inicial era estudar determinadas formas planas, e os alunos perceberam e estabeleceram relações com outras formas espaciais, como a do tetraedro da Figura 13, demonstrando desenvolvimento do pensamento geométrico.


Figura 13: Tetraedros obtidos por meio de dobraduras
A Figura 14 mostra a integração da Matemática com as Artes no desenvolvimento da criatividade durante a pintura das regiões poligonais.


Figura 14: Regiões poligonais do triângulo isósceles
O que se percebe na pintura de alguns trabalhos é como a pandemia impacta a vida dos alunos que estão mais focados nos acontecimentos do mundo e ansiosos pela vacina (Figura 15).


Figura 15: Regiões poligonais do triângulo escaleno
Por orientação do professor, os alunos assistiram ainda a alguns vídeos que envolviam outras atividades com dobraduras, como a criação de uma máscara de pandemia do tipo “coelhinho de Páscoa”, entre outras. Foi solicitado, como atividade complementar, que os alunos escolhessem um dos vídeos e fizessem a criação da dobradura nele apresentada e depois enviassem uma foto da construção feita. As dobraduras feitas por alguns dos alunos podem ser vistas na Figura 16.



Figura 16: Dobraduras temáticas feita por alguns dos alunos da turma
Os alunos gostaram muito da atividade e se empolgaram na construção de diferentes dobraduras temáticas, como a máscara de papel, a espada e a Páscoa.
Considerações
A atividade foi plenamente desenvolvida de forma participativa por todos os alunos que estiveram presentes. Convém destacar que eles acompanharam fielmente o que o professor solicitava, etapa por etapa, chegando ao final da construção pedida.
As gravações permitiram observar que todos os alunos mantiveram as câmeras abertas durante a realização das atividades. Foi possível perceber que, ao final das atividades, os alunos atingiram o objetivo proposto de investigar de que forma as dobraduras auxiliaram no ensino-aprendizagem de formas geométricas.
Um aspecto que poderia ser considerado como negativo é a não presença de alguns alunos para a realização da atividade, aspecto característico de aulas síncronas.
A atividade investigativa oportunizou aos alunos a construção, sem muitas dificuldades, de triângulos e regiões triângulares de diferentes classificações, auxiliando na representação das formas geométricas construídas por meio das dobraduras e nos conceitos matemáticos envolvidos.
A aplicação, em aulas síncronas, de materiais manipulativos, como as dobraduras, não impediu a plenitude da compreensão das atividades propostas. E pôde contribuir na formação do pensamento geométrico e no desenvolvimento de habilidades como a visualização, a atenção e a motricidade, além de ser um material didático de baixo custo.
REFERÊNCIAS
BRASIL. Base Nacional Comum Curricular. Brasília: MEC, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/. Acesso em: 17 set. 2020.
GUTIÉRREZ, A. Visualization in 3-dimensional geometry: In search of a framework. In: PUIG, L.; GUTTIEREZ, A. (eds.). Proceedings of the 20th conference of the international group for the psychology of mathematics education, v. 1, p. 3-19, 1996. Disponível em: https://www.researchgate.net/profile/Angel-Gutierrez-20/publication/267420316_Visualization_in_3-Dimensional_Geometry_In_Search_of_a_Framework/links/54fb47d20cf20700c5e70b17/Visualization-in-3-Dimensional-Geometry-In-Search-of-a-Framework.pdf. Acesso em: 20 jan. 2021.
FROTA, M. C. R. Experiência matemática e investigação matemática. In: CONGRESSO IBERO-AMERICANO DE EDUCAÇÃO MATEMÁTICA (V CIBEM), 5., 2005, Porto. Actas... Porto, 2005. p. 1-10. Disponível em: http://www.matematica.pucminas.br/Eventos/artigos/Maria_Clara_Frota.pdf. Acesso em: 5 jul. 2014.
LEIVAS, J. C. P. Imaginação, intuição e visualização: a riqueza de possibilidades da abordagem geométrica no currículo de cursos de licenciatura de Matemática. 2009. 294f. Tese (Doutorado em Educação) - Universidade Federal do Paraná, Curitiba, 2009. Disponível em: http://www.ppge.ufpr.br/teses/teses/D09_leivas.pdf. Acesso em: 20 jan. 2021.
PONTE, J. P. da; BROCARDO, Joana; OLIVEIRA, Hélia. Investigações matemáticas na sala de aula. 2ª reimp. Belo Horizonte: Autêntica, 2006.
SILVA, M. C. Práticas educacionais na formação inicial do pedagogo baseadas na arte de dobrar papel. Revista Educação Pública, Rio de Janeiro, v. 21, nº 19, 25 de maio de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/19/praticas-educacionais-na-formacao-inicial-do-pedagogo-baseadas-na-arte-de-dobrar-papel. Acesso em: 18 jul. 2022.
SKOVSMOSE, O. C. Desafios da reflexão em Educação Matemática crítica. Campinas: Papirus, 2008.
SOUZA, G. C. de; OLIVEIRA, J. D. S. de. O uso de materiais manipuláveis e jogos no ensino da Matemática. In: X ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, CULTURA E DIVERSIDADE. Anais... Salvador, 7 a 9 de julho de 2010. Disponível em: https://silo.tips/download/x-encontro-nacional-de-educaao-matematica-educaao-matematica-cultura-e-diversida-15. Acesso em: 20 jan. 2021.
Agradecimentos
O presente trabalho foi realizado com apoio da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Capes).
Publicado em 02 de maio de 2023
Como citar este artigo (ABNT)
PASCHOAL, Gilmar Steigleder; BETTIN, Anne Desconsi Hasselmann; LEIVAS, José Carlos Pinto. Regiões poligonais triangulares: uma investigação com dobraduras no Ensino Fundamental. Revista Educação Pública, Rio de Janeiro, v. 23, nº 16, 2 de maio de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/23/15/regioes-poligonais-triangulares-uma-investigacao-com-dobraduras-no-ensino-fundamental
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

