Investigações Matemáticas e Robótica Educacional para o estudo de Geometria Plana nos anos finais do Ensino Fundamental
Jéssica Maria Pereira
Licencianda em Matemática (UFV)
João Vitor Martins Grando
Graduando em Engenharia Elétrica (UFV)
Alexandre Santos Brandão
Doutor em Engenharia Elétrica (UFES) e professor adjunto da UFV
Rejane Waiandt Schuwartz de Carvalho Faria
Doutora em Educação Matemática (Unesp) e professora adjunta da UFV
Robótica Educacional no ensino de Matemática
Com o avanço da informática, a tecnologia ocupa um espaço cada vez mais amplo na atualidade; nele, destacamos o estudo e o desenvolvimento dos robôs. Conforme Mill (2013), a palavra robô vem da palavra tcheca “robotnik”, que quer dizer trabalho árduo. A Robótica refere-se ao desenvolvimento de robôs, que são equipamentos programados para realizar operações de forma autônoma, diferentemente de uma máquina que necessita de um humano para ser operada.
A Robótica foi incluída no campo educacional por volta da década de 1960, pelo pesquisador Seymour Papert. Ele defendeu o uso do computador nas escolas como forma de motivar e incentivar as crianças, pois elas
farão melhor descobrindo (‘pescando’) por si mesmas o conhecimento específico de que precisam; a educação organizada ou informal poderá ajudar mais se certificar-se de que elas estarão sendo apoiadas moral, psicológica, material e intelectualmente em seus esforços. O tipo de conhecimento que as crianças mais precisam e o que as ajudará a obter mais conhecimento (Papert, 2008, p. 135).
Dessa forma, não podemos pensar o ensino da Matemática somente da forma tradicional, caracterizado pela sequência definição, exemplo e exercícios (Faria; Maltempi, 2020). Concordamos que o conhecimento matemático deve ser construído com base no pensar sobre as experiências com objetos e eventos e desenvolvido com a criança agindo sobre eles. Sampaio e Leite (2010, p. 63) ressaltam essa importância, uma vez que “a forma de a educação preparar as pessoas para o mundo tecnológico é fazer do aluno um sujeito reflexivo, que domina a técnica, que tem cultura geral e visão crítica para utilizar a tecnologia com sabedoria”.
Envolvendo as temáticas expostas, relatamos neste artigo a experiência da realização de uma pesquisa pautada na metodologia qualitativa com o objetivo de discutir as contribuições da Robótica Educacional para o ensino de Matemática nos anos finais do Ensino Fundamental na perspectiva das Investigações Matemáticas.
Investigações Matemáticas
A Investigação Matemática por muitos anos foi considerada um campo restrito, visto que, “para os matemáticos profissionais, investigar é descobrir relações entre objetos matemáticos conhecidos ou desconhecidos, procurando identificar as respectivas propriedades” (Ponte; Brocardo; Oliveira, 2003, p. 13). Porém, como alternativa ao ensino tradicional, a Investigação Matemática se mostra como uma metodologia de ensino que coloca o aluno como sujeito ativo, protagonista da sua aprendizagem, ao trabalhar com problemas que revelam uma Matemática interessante.
Nos processos de ensino e de aprendizagem, investigar em Matemática não significa necessariamente formular, testar e provar conjecturas. O ato de investigar está presente quando trabalhamos com questões que interpelam, sejam elas pouco ou muito sofisticadas. Segundo Pólya (1975, p. 7), “a Matemática tem duas faces; é a ciência rigorosa de Euclides, mas é também algo mais... A Matemática em construção aparece como uma ciência experimental, indutiva. Ambos os aspectos são tão antigos quanto a própria Matemática”.
O conceito de Investigação Matemática, no âmbito escolar, ajuda a trazer para a sala de aula o espírito da atividade matemática genuína, constituindo, por isso, uma poderosa metáfora educativa (Ponte; Brocardo; Oliveira, 2003, p. 23). Braumann ressalta a importância da investigação para o desenvolvimento de cidadãos pensantes, autônomos e críticos:
Aprender Matemática não é simplesmente compreender a Matemática já feita, mas ser capaz de fazer investigação de natureza matemática (ao nível adequado a cada grau de ensino). Só assim se pode verdadeiramente perceber o que é a Matemática e sua utilidade na compreensão do mundo e na intervenção sobre o mundo. Só assim se pode realmente dominar os conhecimentos adquiridos. Só assim se pode ser inundado pela paixão “detetivesca” indispensável à verdadeira fruição da Matemática. Aprender Matemática sem forte intervenção da sua faceta investigativa é como tentar aprender a andar de bicicleta vendo os outros andar e recebendo informações sobre como o conseguem. Isso não chega. Para verdadeiramente aprender é preciso montar na bicicleta e andar fazendo erros e aprendendo com eles (Braumann, 2002, p. 5).
Ou seja, o processo de aprendizagem da Matemática deve passar por um processo investigativo, em que o aluno deve atuar como ser ativo. “Sem essa prática, podemos dizer o que quisermos, mas, se formos minimamente honestos, sabemos que não estamos a ensinar Matemática e que o estudante não está a aprender Matemática” (Braumann, 2002, p. 21).
Diante disso, a Investigação Matemática tem se mostrado uma abordagem metodológica eficaz no ensino da Matemática. Na pesquisa que propusemos, os alunos fizeram investigações matemáticas com Robótica Educacional, pois acreditamos que, ao alinhar essas temáticas é possível contribuir para um ensino de Matemática significativo e dinâmico.
Quatro momentos da Investigação Matemática
Para analisar os dados a serem produzidos durante a realização da pesquisa com alunos do 6º ano do Ensino Fundamental, consideramos a interação dos alunos ao longo da realização das atividades de Robótica Educacional para o ensino de Matemática na perspectiva da Investigação Matemática. Segundo Ponte, Brocardo e Oliveira (2003),
a realização de uma investigação matemática envolve quatro momentos principais. O primeiro abrange o reconhecimento da situação, a sua exploração preliminar e a formulação de questões. O segundo momento refere-se ao processo de formulação de conjecturas. O terceiro inclui a realização de testes e o eventual refinamento das conjecturas. E, finalmente, o último diz respeito à argumentação, à demonstração e à validação do trabalho realizado (Ponte; Brocardo; Oliveira, 2003, p. 20).
No primeiro momento destacado pelos autores, identificamos três etapas:
- abrange o reconhecimento da situação; para isso é necessário ler o enunciado, entender do que se trata e contextualizar a pesquisa;
- envolve a exploração preliminar; para tal é necessário coletar informações, olhar o que deve ser respondido e buscar mais informações sobre a situação;
- abrange a formulação de questões; para isso, devem ser elaboradas perguntas que possam auxiliar a encontrar possíveis razões que ocasionaram a situação problema.
No segundo momento, foram elaboradas possíveis respostas ou encaminhamentos para as questões formuladas anteriormente. No terceiro, as hipóteses foram testadas, podendo ser rejeitadas, mantidas, modificadas ou aprimoradas. Finalmente, no último momento, todos os dados obtidos e hipóteses testadas foram agrupados para que se construa uma explicação que seja útil para contribuir como conhecimento científico, ainda que adequada à faixa etária e ao nível escolar.
Com base nos momentos descritos por Ponte, Brocardo e Oliveira (2003), analisamos como os alunos, ao longo da pesquisa, percorreram essas etapas na realização das atividades propostas. Contudo, antes da análise de dados, apresentamos a metodologia e os procedimentos adotados para realização da pesquisa.
Figuras geométricas planas: triângulo e quadrado
A Geometria Plana se concentra em estudar conceitos geométricos primitivos, como ponto, reta e plano, além de figuras bidimensionais, ou seja, que possuem comprimento e largura, com seus perímetros e áreas.
Dentre as figuras geométricas planas, nesta pesquisa o foco está nos triângulos e quadrados. Os triângulos são polígonos que, “dados três pontos, A, B e C, não colineares, à reunião dos segmentos AB, AC e BC chama-se triângulo ABC” (Dolce; Pompeo, 2005, p. 36). O quadrado, que também é um polígono, é um quadrilátero notável plano e convexo “se, e somente se, possui os quatro ângulos congruentes e os quatro lados congruentes” (Dolce; Pompeo, 2005, p. 101).
De acordo com a BNCC, “a Geometria envolve o estudo de um amplo conjunto de conceitos e procedimentos necessários para resolver problemas do mundo físico e de diferentes áreas do conhecimento” (Brasil, 2018, p. 271). Assim, a escolha por essas figuras geométricas se justifica nesta pesquisa, pois são importantes para que o aluno tenha noção sobre questões oriundas do cotidiano, além de estar entre as principais estudadas no 6º ano do Ensino Fundamental, o que configura os sujeitos desta investigação.
Metodologia e procedimentos
A pesquisa realizada é de caráter qualitativo, pois “lida e dá atenção às pessoas e às suas ideias, procura fazer sentido de discursos e narrativas que estariam silenciosas” (D’Ambrosio, 2004, p. 19). Na experiência relatada neste artigo, o caráter qualitativo se mostra pertinente, pois se preocupa com os dados coletados de forma pessoal e interpretativa.
O público-alvo foram os alunos do 6º ano do Ensino Fundamental da Escola Estadual Raul de Leoni, na cidade de Viçosa/MG. Os registros foram realizados a partir das fotografias dos encontros, das folhas de atividades resolvidas pelos estudantes e do caderno de campo.
Esclarecemos que, antes do início da produção de dados desta pesquisa, ela foi aprovada pelo Comitê de Ética em Pesquisa com Seres Humanos da Universidade Federal de Viçosa (CAAE 67403223.0.0000.5153), e os termos de assentimento livre e esclarecido (TALE) foram entregues, lidos e assinados pelos participantes e por seus responsáveis para a autorização da divulgação científica dos dados produzidos.
O robô utilizado na pesquisa foi desenvolvido no Núcleo de Especialização em Robótica (NERO), ligado ao Departamento de Engenharia Elétrica da UFV, coordenado pelo professor Dr. Alexandre Santos Brandão. O NERO atua desde 2010 com o objetivo de introduzir os conceitos e aplicações da área de Robótica. Ao longo dos anos, o núcleo passou por expansões significativas, permitindo o acesso de estudantes de diversos cursos e a realização de parcerias com professores de outros departamentos da UFV. Atualmente, o principal objetivo do NERO é capacitar recursos humanos especializados nas áreas de controle, automação, eletrônica, informática e educação.
Além disso, a pesquisa contou com a colaboração do Grupo de Atenção às Tecnologias Digitais (GATE), que surgiu em 2013 da vontade de criação de um espaço de estudo, reflexão e pesquisa no Departamento de Educação da Universidade de Viçosa. As professoras Dra. Silvana Claudia dos Santos (Departamento de Educação) e Dra. Rejane Waiandt Schuwartz de Carvalho Faria (Departamento de Matemática) coordenam o grupo, que realiza encontros periódicos de estudo sobre temas relevantes no que tange às tecnologias e à educação. Especificamente para a pesquisa aqui relatada, as atividades passaram por um processo de avaliação e revisão em reuniões do grupo.
Esses grupos têm em comum o projeto Robótica na Educação Básica: Possibilidades e Desafios para o Ensino e Aprendizagem de Matemática, coordenado pelos professores Dr. Alexandre Brandão, Dra. Silvana Santos e Dra. Rejane Faria.
Foram realizados dois encontros presenciais, com duração de 1h 40min cada, empregando atividades de construção de figuras planas a partir de comandos de programação com o Robô Esteira viabilizadas pela utilização do aplicativo TagBot no celular (Figura 1). As atividades, intituladas Investigando Triângulos e Investigando Quadrados, abordam questões que fomentam o desenvolvimento e a exploração do raciocínio lógico (Pereira, 2023). Nessas atividades, são trabalhados os conceitos de construção de figuras planas, ângulos internos, unidades de medida e programação.

Figura 1: Robô esteira
Assim, as questões foram planejadas de modo que os alunos explorassem e conhecessem um pouco mais sobre quadrados e triângulos por meio do robô esteira. Os dois encontros presenciais ocorreram no horário regular de aula dos alunos, durante o mês de maio de 2023.
O aplicativo TagBot para smartphones Android (Figura 2) foi desenvolvido para controle das funções do robô esteira pelo aluno de iniciação científica João Vitor Martins Grando, do curso de bacharelado em Física da UFV, sob orientação do professor Alexandre Brandão. A proposta do app consiste em utilizar smartphone do sistema operacional Android para comandar sem fio o robô, por meio do protocolo Bluetooth, de forma a facilitar o controle. O aplicativo foi desenvolvido para tornar o trabalho intuitivo e de fácil acesso aos estudantes. Toda a arquitetura do sistema foi desenhada com o objetivo de simplificar a comunicação entre aluno, aplicativo e robô. O aplicativo foi instalado no smartphone dos pesquisadores e operado pelas crianças ao longo dos encontros.

Figura 2: Interface do aplicativo TagBot
O aplicativo conta com diferentes funções, particionadas em módulos que foram implementados separadamente. Quatro módulos foram criados: o digital, o joystick, o giroscópio e o geometria. Inicialmente, o estudante interage com a tela inicial selecionando o módulo que será trabalhado. Após inserir o módulo, o aluno é transferido para o painel de tarefas, onde poderá programar o robô.
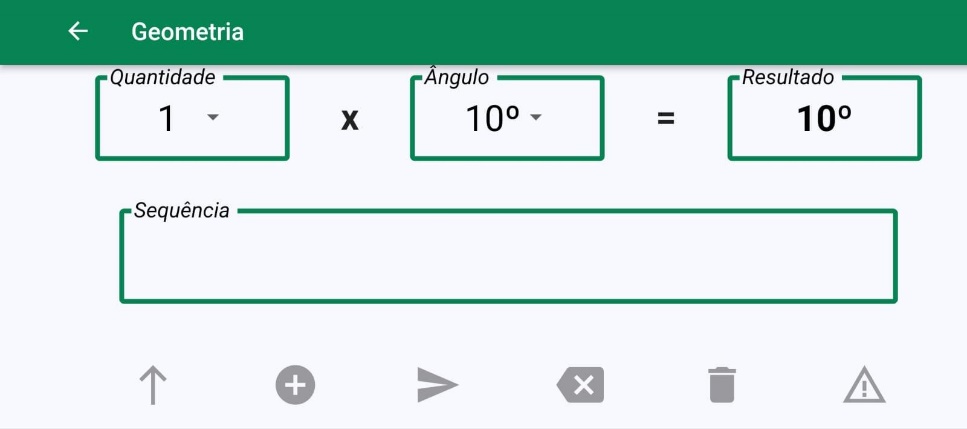
Figura 3: Tela do módulo Geometria do aplicativo TagBot
Na pesquisa realizada, trabalhamos com o módulo geometria, que consiste na escolha de ângulos e movimentos para a construção de figuras planas. São disponibilizadas aos alunos, na aba ângulo, as opções de 10º, 12º e 15º em conjunto; são disponibilizados, na aba quantidade, múltiplos de 1 a 10. Sendo selecionados determinados ângulo e múltiplo, o aluno pode visualizar na aba resultado a solução da multiplicação, que será o possível ângulo de rotação do robô. O aplicativo também conta com ferramentas para programação: andar para a frente, virar ângulo, executar, apagar código, limpar código e parar execução. Está disponível ao aluno a visualização da programação inserida no quadro sequência. Apresentados à metodologia e aos procedimentos adotados para realização da pesquisa, passamos a apresentar, na próxima seção, a análise de dados.
Esclareço que foram usados nomes fictícios para os alunos que participaram da coleta de dados, de modo a preservar suas identidades. As falas estão dispostas com recuo e em itálico, para facilitar a identificação ao longo do texto, salvo em alguns trechos pequenos, que estão em itálico e entre aspas ao longo dos parágrafos, para evitar quebra na leitura. Esses trechos foram extraídos das atividades e dos registros no caderno de campo; contudo, existem interferências nossas nas falas, que são acrescentadas entre colchetes [ ], com o intuito de dar sentido para o leitor.
Apresentação e discussão dos resultados
Para a realização da atividade Investigando Triângulos, foi solicitado que os alunos se colocassem em duplas, sendo entregue a cada aluno régua, transferidor, tesoura, cola e a folha da atividade. Foi realizada a leitura do enunciado da questão 1 (Quadro 1), que consistia em desenhar um triângulo qualquer e medir seus ângulos internos com o auxílio de instrumentos de construção geométrica, mais precisamente régua e transferidor.
Quadro 1: Questão 1 da atividade Investigando Triângulos
Com auxílio de instrumentos de construção geométrica (régua e transferidor), vamos investigar triângulos:
a) Desenhe um triângulo qualquer e meça os seus ângulos internos.
b) Qual é o valor da soma das medidas desses ângulos?
c) Compare o valor obtido com os que
Após a leitura do enunciado, os alunos foram questionados sobre o que seria um triângulo e onde se localizariam seus ângulos internos. Dois alunos responderam:
Maria: É aquela figura assim [desenhando no ar um triângulo].
Antônio: Ângulo interno é aquele que fica na beiradinha.
As respostas dos alunos mostram uma descrição em linguagem coloquial, própria deles, mas que evidencia uma apropriação dos objetos em discussão. Para medir os ângulos internos do triângulo solicitado no item a da questão 1, foi observado que os alunos permaneceram inertes, evidenciando que não sabiam utilizar o transferidor. Diante dessa atitude, foi desenhado um triângulo no quadro e, com o auxílio do transferidor, foi explicado aos alunos como utilizá-lo. Como exemplo, foi feita a medição dos ângulos internos do triângulo desenhado, solicitando a participação da turma e registrando as soluções na lousa.

Figura 4: Orientação da questão 1 da atividade Investigando Triângulos
No item b da questão 1, foi pedido aos alunos que realizassem a soma das medidas dos ângulos internos do triângulo que haviam desenhado, porém nem todos os alunos encontraram o valor de 180°, o que acabou gerando preocupação em alguns alunos, achando que estavam errados em seus cálculos. Uma aluna comentou: “O meu não deu o mesmo número!”. Sua colega logo interveio e a ajudou a conferir suas medições. Esse fato evidencia a participação ativa dos alunos, pois mostra que eles estavam realizando comparações e buscando uma justificativa para a igualdade. Evidencia ainda a aprendizagem significativa, pois, segundo Aquino (2007, p. 6),
a aprendizagem refere-se à aquisição cognitiva, física e emocional, e ao processamento de habilidades e conhecimento em diversas profundidades, ou seja, o quanto uma pessoa é capaz de compreender, manipular, aplicar e /ou comunicar esse conhecimento e essas habilidades.
Nessa etapa, dentre os quatro momentos da Investigação Matemática descritas por Ponte, Brocardo e Oliveira (2003), os alunos estavam passando pelo reconhecimento da situação, pois estavam explorando e formulando questões oriundas de uma problemática.
O acontecido deu abertura para introdução do item c da questão 1, que vislumbrava uma discussão perante a comparação dos valores encontrados. Os alunos, ao serem solicitados que descrevessem o que haviam observado, apresentaram dificuldade em registrar suas ideias, embora compreendessem e relatassem oralmente o que estavam pensando. Alguns alunos aguardavam o registro do colega ao lado para que pudessem escrever o mesmo. Com o objetivo de estimular a escrita dos alunos, foi indagado: “Os triângulos que vocês desenharam são iguais? E a soma obtida?”. Alguns alunos responderam.
Tereza: Eu acho que o meu está mais “fino” e o dela mais “achatado”.
Wilson: O meu está mais bonito porque está mais reto, maior.
As respostas dos alunos (Quadro 2) evidenciam uma compreensão adequada do conteúdo. Na socialização das respostas da questão, enfatizou-se que, para qualquer triângulo que eles desenhassem, a soma dos ângulos internos seria 180°, mas que seriam aceitas medições com pequenas variações de ângulos de até 2º, para mais ou para menos, devido à pouca habilidade que tinham e à imprecisão dos materiais de construção geométrica utilizados.
Quadro 2: Respostas dos alunos à letra c da questão 1 da atividade Investigando Triângulos

Reprodução das respostas, com correção ortográfica:
Os ângulos são diferentes, mas os resultados obtidos são os mesmos.
Os números são diferentes, mas obtivemos a mesma soma.
Para a realização da segunda questão (Quadro 3), foi distribuído para cada aluno um triângulo feito em papel cartão com os respectivos ângulos internos marcados. Foi solicitado que os alunos recortassem o triângulo recebido em três partes, de modo que cada parte tivesse apenas um ângulo do triângulo inicial.
Quadro 3: Questão 2 da atividade Investigando Triângulos
Recorte o triângulo que você recebeu em três partes (de forma que cada parte tenha apenas um ângulo do triângulo inicial). Depois una os três ângulos de forma que fiquem adjacentes ao redor de um vértice e cole no espaço abaixo. Qual valor do ângulo formado pela união dos três ângulos do triângulo inicial?
Após o recorte, foi solicitado que os alunos fizessem um ponto no espaço em branco disponível abaixo do enunciado da questão. Nesse momento, foi explicado o conceito de vértice e pedi que cada aluno unisse, em uma colagem, os ângulos de forma adjacente ao redor do vértice. O objetivo da tarefa era permitir aos alunos a visualização do ângulo de 180º pela soma dos ângulos internos de um triângulo qualquer. Logo após a colagem, foi solicitada a medição do ângulo formado pela união dos três ângulos provenientes do triângulo inicial (Quadro 4). No primeiro momento, os alunos resolveram utilizar o transferidor; apenas uma aluna respondeu, somente observando, que o resultado seria 180°. Ao longo dessas questões, os alunos estavam trabalhando em ideias pertinentes a dois momentos da Investigação Matemática descritas por Ponte, Brocardo e Oliveira (2003): a formulação de conjecturas e a realização de testes. Afirmamos isso porque era possível observar os alunos organizando os dados, fazendo testes e afirmações sobre as conjecturas, reformulando ideias e refinando as conjecturas previamente elaboradas.
Quadro 4: Respostas dos alunos à Questão 2 da atividade Investigando Triângulos

A proximidade do horário de intervalo prejudicou o desenvolvimento da questão 2, visto que gerou inquietude na turma, ocasionando consequentemente desatenção à aula. Logo após o término dessa questão, os alunos foram liberados para o intervalo. No retorno, fizemos a terceira questão (Quadro 5), que consistia em desenhar um triângulo equilátero utilizando como instrumento o Robô Esteira, que realiza movimentos de 10, 12 e 15 graus.
Quadro 5: Questão 3 da atividade Investigando Triângulos
Sabendo que o robô realiza movimentos de 10°, 12º e 15º, programe-o para desenhar um triângulo equilátero (possui três ângulos de mesma medida). Quais foram os processos realizados?
Visando ensinar os alunos a manipular o aplicativo TagBot, foi realizada uma ilustração na lousa representando a tela do aplicativo e explicados os comandos da programação. Os alunos, em consenso, optaram por trabalhar com o ângulo de 10° e, com o objetivo de estimulá-los, foi feita a pergunta: “Qual será o valor de cada ângulo interno?”. Nesse momento os alunos ficaram pensativos, até que uma aluna ressaltou: “Será 60°”.
Para entendimento e acompanhamento de todos os alunos, foi explicado que, como a soma dos ângulos internos de um triângulo qualquer é 180º e como estávamos à procura do valor de cada ângulo interno do triângulo equilátero, que possui todos os ângulos de mesma medida, bastava realizar a divisão de 180º por 3 para descobrir o valor de cada ângulo interno. Após saberem a medida do ângulo, foi perguntado qual seria o múltiplo de 10 a ser trabalhado, e os alunos rapidamente responderam que seria 6. Então foi perguntado qual seria a sequência trabalhada, e observamos que os alunos permaneceram inertes, evidenciando que eles não sabiam o que era para fazer. Diante dessa atitude, apresentei, por meio da construção, o passo a passo de um desenho do triângulo, enfatizando quais seriam os processos que deveriam ser realizados, solicitando a participação da turma e registrando a programação na lousa. Como os alunos demonstraram entendimento, seguimos para a parte prática.
Foi pedido que os alunos se reunissem no fundo da sala, de onde as carteiras foram retiradas para haver espaço para trabalhar com o robô. Os próprios alunos se organizaram, possibilitando que todos tivessem contato com o aplicativo TagBot.

Figura 5: Alunos realizando a questão 3 da atividade Investigando Triângulos
Para a resolução da quarta questão (Quadro 6), foi solicitado que os alunos voltassem às carteiras.
Quadro 6: Questão 4 da atividade Investigando Triângulos
Investigue as possibilidades de realizar a mesma figura da questão acima utilizando outra combinação entre os valores dos ângulos de 10°, 12° e 15°. Registre aqui as combinações que utilizaram.
Com o objetivo de investigar as possibilidades de realizar a mesma figura utilizando os demais ângulos, foi aberta uma discussão. Os alunos foram indagados sobre quais eram as possibilidades, se é que havia, de trabalhar com os ângulos de 12° e 15°. Envolvidos na atividade, eles responderam quais seriam os possíveis múltiplos de 12° e 15°. Ao perguntar sobre a sequência, os participantes observaram que seria a mesma que a trabalhada com o ângulo de 10º, mudando apenas os valores dos múltiplos e dos ângulos. Novamente foi solicitado que os alunos caminhassem ao fundo da sala, onde cada aluno teve a oportunidade de programar o robô com o ângulo e múltiplo escolhido (Quadro 7).
Quadro 7: Respostas dos alunos – Questão 4 da atividade Investigando Triângulos

Descrição das respostas com correção ortográfica:
[Utilizando] a multiplicação e a Matemática. 5x12=60 e 6x10=60.
Usei os múltiplos 6 e 5 e os ângulos de 10º e 12º, resultando em 60º.
Ao longo das questões 3 e 4, foi possível observar o interesse dos alunos pela atividade, pois eles manipulavam o aplicativo tecendo comentários com os colegas sobre a programação e estavam atentos à figura formada pelo robô. Considero que o modo descontraído e a linguagem informal da programação utilizada no aplicativo estimularam e facilitaram o desenvolvimento da atividade.
Principalmente na etapa de manipulação do robô esteira, foi possível identificar que os alunos estavam no quarto momento da Investigação Matemática. Finalizando a realização da atividade, os alunos estavam no momento de validação do trabalho, pois estavam dedicados a justificar as conjecturas e a avaliar o raciocínio e os resultados encontrados (Ponte; Brocardo; Oliveira, 2003).
Porém, destacamos a dificuldade que os alunos tiveram em registrar a solução dessas questões. Muitos não tiveram dedicação para responder; escreveram textos curtos, demonstrando desinteresse para escrever. Rosale (2018, p. 15) fala da "dificuldade de muitos alunos para justificar seu raciocínio ou até mesmo seguir uma linha básica de argumentação" no âmbito da Matemática escolar. Assim como o autor, acreditamos que isso tenha relação com a falta de acesso a questões discursivas no ensino da Matemática, visto que os alunos relataram oralmente o que era pedido nas questões, mostrando compreensão do conteúdo.
De modo geral, no decorrer da atividade Investigando Triângulos, todos estavam atentos, realizaram as construções solicitadas, acompanharam atentamente a aula e mostraram-se interessados na resolução das questões.
No encontro seguinte, realizamos a atividade Investigando Quadrados. Inicialmente foi solicitado que os alunos se organizassem em duplas, sendo entregue a cada aluno régua, transferidor, tesoura, cola e a folha da atividade. Para iniciar, foi realizada a leitura do enunciado da questão 1 (Quadro 8), que consistia em desenhar um quadrado e medir seus ângulos internos com o auxílio de instrumentos de construção geométrica, mais precisamente régua e transferidor.
Quadro 8: Questão 1 da atividade Investigando Quadrados
Com auxílio de instrumentos de construção geométrica (régua e transferidor), vamos investigar quadrados:
- Escolha uma medida e desenhe um segmento AB que será o lado de um quadrado ABCD.
- Construa um ângulo reto em cada uma das extremidades do seguimento construído no item anterior.
- Com a mesma medida utilizada no item a, construa os segmentos AD e BC, mantendo o ângulo reto em cada vértice.
- Una os vértices D e C. Observe que foram formados o segmento DC e o quadrado ABCD.
- Quais as medidas de cada um dos quatro ângulos internos formados?
- Qual é o valor da soma das medidas desses ângulos?
- Pense em uma definição de quadrado. Converse com seus colegas sobre o que você pensou e registre a definição a que chegaram de forma colaborativa.
Na realização desta questão, percebemos que muitos alunos apresentaram dificuldades em trabalhar com a régua; a maioria da turma acreditava que a medição das unidades começava a partir do número um. Ao perceber essa dificuldade, pedimos que os alunos contassem os intervalos entre as numerações da régua; todos os alunos utilizavam uma régua de 30cm. Ao contarem, os alunos perceberam que havia 29cm. Dessa forma, logo entenderam o porquê de a medição começar no zero. Diante da dificuldade dos alunos ao realizar a questão 1, foi necessário orientá-los nos itens a, b, c e d. Ao final do item d, vislumbrando a compreensão do conteúdo, foi realizada a construção pedida no quadro com a colaboração dos alunos, que permaneceram atentos à explicação.
No item e da questão 1, foi pedido aos alunos que medissem cada um dos ângulos internos do quadrado. Apesar de terem realizado a construção da figura partindo do ângulo de 90°, os alunos realizaram a medição com o auxílio do transferidor, medindo cada um dos ângulos internos. O item f da questão 1 solicitava o valor da soma das medidas dos ângulos internos; os alunos rapidamente souberam responder. Nos itens e e f, foi possível notar que os alunos tiveram mais facilidade em trabalhar com o transferidor e em entender os conceitos abordados nas atividades em comparação com a primeira aula, Investigando Triângulos.
O item g da questão 1 solicitava uma discussão em grupo de forma colaborativa que tinha por objetivo uma breve dissertação sobre a definição de quadrado. Como havíamos notado um distanciamento da turma em relação às questões discursivas, estimulamo-los com a pergunta: “O que vocês observam em relação aos lados e aos ângulos? Eles têm a mesma medida?”. As respostas dos alunos (Quadro 9) mostram uma descrição em linguagem coloquial que evidencia compreensão adequada do resultado obtido.
Quadro 9: Respostas dos alunos à letra g questão 1 da atividade Investigando Quadrados

Reprodução das respostas com correção ortográfica:
Um quadrado tem quatro ângulos que medem 90º, tem vértices, arestas, faces e quatro lados que medem 90º [acreditamos se referir à mesma medida].
Quatro lados de mesma medida e quatro ângulos de 90º.
Assim como ocorreu na atividade com triângulos, nessa atividade, ao longo da primeira questão, os alunos estavam no momento de reconhecimento da situação da Investigação Matemática (Ponte; Brocardo; Oliveira, 2003). Construindo quadrados, eles exploravam e formulavam ideias relevantes para compreensão da problemática trabalhada.
Para a realização da questão 2, foi distribuído para cada aluno um quadrado feito em papel cartão com os respectivos ângulos internos marcados. A questão 2 (Quadro 10) solicitava que os alunos recortassem o quadrado recebido em quatro partes, de modo que cada parte tivesse apenas um ângulo do quadrado inicial.
Quadro 10: Questão 2 da atividade Investigando Quadrados
Recorte o quadrado que você recebeu em quatro partes (de forma que cada parte tenha apenas um ângulo do quadrado inicial). Depois una os quatro ângulos de forma que fiquem adjacentes ao redor de um vértice e cole no espaço abaixo. Qual valor do ângulo formado pela união dos quatro ângulos do quadrado inicial?
Após o recorte, foi solicitado que os alunos unissem, em uma colagem, os ângulos de forma adjacente ao redor do vértice. O objetivo da questão era permitir aos alunos a visualização do ângulo de 360° pela soma dos ângulos internos de um quadrado qualquer. Logo após a colagem, foi solicitada a medição do ângulo formado pela união dos quatro ângulos provenientes do quadrado inicial. Nesse momento, todos os alunos disseram 360°; com o objetivo de os alunos expressarem o raciocínio, foi perguntado: “Como vocês souberam sem realizar as medições?”. Dois alunos responderam:
Sebastiana: Esse quadrado é “igual” ao que acabamos de medir [se referindo aos ângulos].
José Lúcio: Porque formou uma bolinha [se referindo a uma volta completa do transferidor].
Essas respostas evidenciam a compreensão do conteúdo, apesar da linguagem coloquial. Os alunos se apropriaram dos conceitos matemáticos por meio de suas experiências; como defendido por Bishop (1991), a Educação Matemática deve ser um processo de enculturação, um envolvimento com a Matemática, uma apropriação dos objetos da cultura matemática construída ao longo da história humana. Esse processo é interpessoal e ocorre essencialmente nas interações professor-aluno e aluno-aluno.

Figura 6: Alunos realizando a questão 2 que compõem a atividade Investigando Quadrados
Logo após o término da questão, os alunos foram liberados para o intervalo. Uma observação que nos causou espanto foi o fato de os alunos não quererem participar do intervalo; eles estavam entusiasmados com a possibilidade de manipular o robô novamente. Após o professor da turma conversar com os alunos, eles aceitaram ir, com a promessa de que, na sequência, teriam a oportunidade de manipulá-lo. No retorno, resolvemos a terceira questão (Quadro 11), que consistia em desenhar um quadrado utilizando como instrumento o robô esteira, que realiza movimentos de 10, 12 e 15 graus.
Quadro 11: Questão 3 da atividade Investigando Quadrados
Sabendo que o robô realiza movimentos de 10°, 12º e 15º, programe-o para desenhar um quadrado. Quais foram os processos realizados?
Para relembrar os alunos de como manipular o aplicativo TagBot, foi feita uma ilustração no quadro representando a tela do aplicativo e foi explicada novamente a programação. Porém, dessa vez, os alunos tiveram mais facilidade; antes mesmo de serem perguntados, já expressavam a sequência e o múltiplo a ser trabalhado. Os alunos, em consenso, optaram por trabalhar com o ângulo de 10°, relatando que o múltiplo seria 9. Então foi perguntado: “Por que a sequência é essa?”, e os alunos responderam:
Elisabete: Para fazer o triângulo, utilizamos três vezes [se referindo ao conjunto de comandos da programação], então pro quadrado é quatro.
Andrey: A gente tem que formar esse desenho aqui [apontando para a construção do quadrado feito na questão 1], então precisa fazer assim! [passando o dedo por cada lado do quadrado].
Essas falas e as discussões ocorridas ao longo da atividade revelam que os alunos estavam empenhados em organizar os dados, fazendo e testando afirmações, elaborando e reelaborando conjecturas e ideias. Esse comportamento é característico dos momentos de formulação de conjecturas e realização de testes, conforme argumentam Ponte, Brocardo e Oliveira (2003).
Dando continuidade à questão 3, foi solicitado que os alunos se reunissem no fundo da sala, onde as carteiras foram retiradas para haver espaço para trabalhar com o robô. Os alunos se organizaram por contra própria, em ordem numérica, o que possibilitou que cada aluno pudesse ter contato e programar o robô via aplicativo.

Figura 7: Alunos realizando a questão 3 da atividade Investigando Quadrados
Para a resolução da questão 4 (Quadro 12), foi solicitado que os alunos voltassem para as carteiras.
Quadro 12: Questão 4 da atividade Investigando Quadrados
Investigue as possibilidades de realizar a mesma figura da questão acima utilizando outra combinação entre os valores dos ângulos de 10°, 12° e 15°. Registre aqui as combinações que utilizaram.
Com o objetivo de investigar as possibilidades de realizar a mesma figura com os demais ângulos, foi aberta uma discussão em que perguntamos quais eram as possibilidades, se é que havia, de trabalhar com os ângulos de 12° e 15°. Para o ângulo de 15°, os alunos logo expressaram que o múltiplo trabalhado seria 6, porém para o ângulo de 12° os alunos falavam valores sem muita reflexão. Visando ao entendimento da turma, escrevemos na lousa as multiplicações 12x7 e 12x8, realizando-as com a colaboração dos alunos. Ao observarem que os resultados eram 84 e 96, a maior parte da turma percebeu que não seria possível trabalhar com esse ângulo, porém alguns alunos continuaram dizendo valores aleatórios. Esse fato evidencia a memorização sem compreensão da tabuada, o que ocasiona prejuízos para a aprendizagem. Segundo Prieto (2006, p. 1),
compreender é fundamental. É inconcebível exigir que os alunos recitem: "duas vezes um, dois; duas vezes dois, quatro;...", sem que tenham entendido o significado do que estão dizendo. Na multiplicação, bem como em todas as outras operações, a noção de número e o sistema de numeração decimal precisam ser construídos e compreendidos.
Novamente, foi solicitado que os alunos caminhassem até o fundo da sala para que pudessem manipular o robô, cada aluno realizaria a programação. No decorrer da questão 4, foi possível observar a participação e a colaboração dos estudantes, que se mantiveram interessados durante toda a questão.

Figura 8: Alunos realizando a questão 4 da atividade Investigando Quadrados
Quadro 13: Resposta dos alunos à questão 4 da atividade Investigando Quadrados

Reprodução das respostas com correção ortográfica:
Não tem como trabalhar com o ângulo de 12º, porque não tem número que multiplica [ou seja, 90 não é múltiplo de 12].
O doze não tem como. O 15 tem como com o 6 [pois 6x15=90].
Todos os alunos tiveram oportunidade de programar o robô. Durante a realização dessa atividade, os alunos estavam focados em investigar matematicamente as figuras geométricas. A cada construção, novas descobertas surgiam e eram compartilhadas com os colegas da turma. Assim, o conhecimento era construído de forma coletiva. Identificamos, portanto, que os alunos estavam no quarto momento da Investigação Matemática, a validação do trabalho, pois estavam justificando as conjecturas e avaliando o raciocínio e os resultados encontrados (Ponte; Brocardo; Oliveira, 2003).
Em seguida, foi solicitado que voltassem para suas carteiras, sendo distribuída uma folha em branco para cada estudante. Foi pedido que os alunos fizessem um desenho que expressasse o que a aula havia representado para eles. Alguns dos desenhos estão registrados a seguir (Quadro 14).
Quadro 14: Desenhos realizados pelos alunos
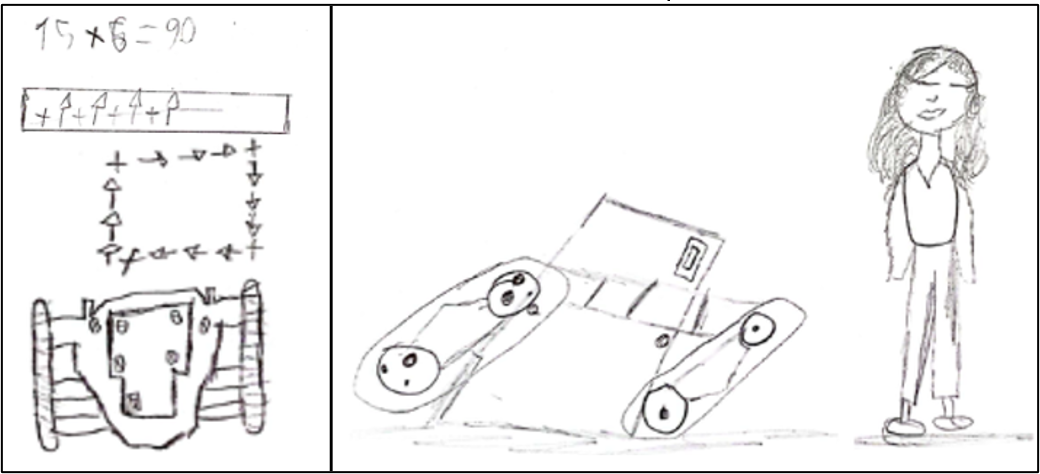
De modo geral, no decorrer dessa atividade, todos estavam atentos, realizando as construções solicitadas, acompanhando a aula e mostrando-se interessados na resolução das questões.
Considerações finais
No trabalho realizado, a Robótica foi utilizada em prol do ensino de Matemática. Por meio do aplicativo TagBot para celular Android e do robô esteira, foram explorados os conceitos de construção das figuras planas triângulo e quadrado e seus ângulos internos por meio da Investigação Matemática. As respostas obtidas durante a aplicação da atividade demonstraram que a Robótica Educacional desempenhou papel importante como forma de comunicação e interação.
A partir da experiência realizada, podemos concluir que esses resultados foram positivos para os quatro momentos da Investigação Matemática. Afirmamos isso porque os alunos reconheceram a situação e buscaram informações que lhes ajudariam nos próximos passos. Além disso, os alunos formularam conjecturas sobre a soma dos ângulos internos de triângulos e quadrados. Fizeram, ainda, testes sobre as conjecturas formuladas. Por fim, os alunos argumentaram quanto aos resultados obtidos.
Ao longo do desenvolvimento da atividade, a comunicação estabelecida criou um ambiente pedagógico interativo, colaborativo e acolhedor. Esse espaço de comunicação proporcionou a interação e motivou os alunos a participar ativamente da atividade, condições essenciais para a enculturação matemática dos alunos (Bishop, 1991).
Os estudantes que estão atualmente nos anos finais do Ensino Fundamental são crianças com as quais a tecnologia está sempre presente. Portanto, ao utilizar a Robótica, foi possível aproximar os alunos da cultura da Matemática por meio das tecnologias digitais, motivando os alunos a participar das atividades propostas. Dessa forma, a Robótica, em conjunto com as atividades, desempenhou papel essencial no desenvolvimento de uma atitude positiva das crianças em relação à Matemática.
Com a realização das atividades, constatamos que a Robótica possui a capacidade de proporcionar discussões matemáticas sobre construção de figuras planas, instigar a curiosidade dos alunos, possibilitar a generalização matemática e motivar a interação entre alunos e professores em momentos de discussão das atividades. Além disso, a robótica contribuiu para que o aluno compreendesse o que foi trabalhado nas atividades, possibilitando o enriquecimento dos processos de ensino e de aprendizagem, favorecendo a construção de conhecimentos.
Referências
AQUINO, C. de. Como aprender: Andragogia e as habilidades de aprendizagem. São Paulo: Pearson Prentice Hall, 2007.
BISHOP, A. J. Mathematical enculturation: A cultural perspective on mathematics education. The Netherlands: Kluwer Academic, 1991.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, 2018.
BRAUMANN, C. Divagações sobre Investigação Matemática e o seu papel na aprendizagem da Matemática. In: PONTE, J. P.; COSTA, C.; ROSENDO, A. I.; MAIA, E.; FIGUEIREDO, N; DIONÍSIO, A. F. (eds.). Atividades de investigação na aprendizagem da Matemática e na formação de professores. Lisboa: SEM-SPCE, 2002.
D’AMBROSIO, U. Prefácio. In: Borba, M.; Araújo, J. (eds.). Pesquisa qualitativa em Educação Matemática. Belo Horizonte: Autêntica, 2004. p. 11-23.
DOLCE, O.; POMPEO, J. N. Fundamentos de Matemática Elementar. Vol. 9 – Geometria Plana. São Paulo: Atual, 2005.
FARIA, R. W. S, C.; MALTEMPI, M, V. Raciocínio proporcional na Matemática escolar. Revista Educação em Questão, Natal, v. 58, nº 57, p. 1-18, set. 2020.
MILL, D. (org.). Escritos sobre educação: desafios e possibilidades para ensinar e aprender com as tecnologias emergentes. São Paulo: Paulus, 2013.
MORAN, J. M.; MASETTO, M.; BEHRENS, M. Novas tecnologias e mediação pedagógica. São Paulo: Papirus, 2003.
PAPERT, S. A máquina das crianças: repensando a escola na era da informática. Porto Alegre: Artes Médicas, 2008.
PEREIRA, J. Robótica Educacional no ensino de Matemática nos anos finais do Ensino Fundamental. Monografia (Licenciatura em Matemática) - Universidade Federal de Viçosa, Viçosa, 2023.
PÓLYA, G. A arte de resolver problemas. Trad. H. L. Araújo. Rio de Janeiro: Interciência 1975. (Edição original de 1945.)
PONTE, J. P.; BROCARDO, J.; OLIVEIRA, H. Investigações Matemáticas na sala de aula. Belo Horizonte: Autêntica, 2003.
ROSALE, A. R. Argumentação e prova matemática na Educação Básica. Dissertação (Mestrado Profissional em Ensino de Matemática) - Universidade de São Paulo, São Paulo, 2018.
SAMPAIO, M. N.; LEITE, L. S. Alfabetização tecnológica do professor. Petrópolis: Vozes, 2011.
Publicado em 03 de setembro de 2024
Como citar este artigo (ABNT)
PEREIRA, Jéssica Maria; GRANDO, João Vitor Martins; BRANDÃO, Alexandre Santos; FARIA, Rejane Waiandt Schuwartz de Carvalho. Investigações Matemáticas e Robótica Educacional para o estudo de Geometria Plana nos Anos Finais do Ensino Fundamental. Revista Educação Pública, Rio de Janeiro, v. 24, nº 32, 3 de setembro de 2024. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/24/32/investigacoes-matematicas-e-robotica-educacional-para-o-estudo-de-geometria-plana-nos-anos-finais-do-ensino-fundamental
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
1 Comentário sobre este artigo
Deixe seu comentárioExcelente artigo! Estou utilizando como referência em vários projetos e nas minhas aulas na escola. O conteúdo é muito bem estruturado e claro, o que facilita bastante o aprendizado dos meus alunos. A abordagem dos temas é completa e atual, o que tem contribuído de forma significativa para o desenvolvimento dos nossos estudos. Com certeza continuarei usando este material como apoio nas minhas aulas. Parabéns pelo trabalho!
Este artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

