A Matemática e o som

Desenvolver conteúdos de Matemática com frações em sala de aula tem sido um desafio para docentes que trabalham no Ensino Fundamental. De acordo com Bertoni (2009), o ensino-aprendizagem a respeito do tema tem apresentado inúmeros problemas devido aos métodos de ensino que ainda são usados no espaço escolar.

Geralmente, o conceito de todo/parte é abordado por meio de figuras geométricas planas, divididas e pintadas. Muitas vezes, essas figuras são desenhadas no quadro e copiadas no caderno, tornando-se difícil respeitar as relações de distâncias, por exemplo. Consequentemente, é comum o aluno não compreender o conceito, comprometendo sua aprendizagem.

A notação de uma fração, assim como de suas operações básicas são de difícil aprendizagem para alunos do 6º ano. Com isso, os discentes acumulam dificuldades e chegam aos anos finais do Ensino Fundamental sem dominar as noções básicas desse conteúdo, o que para eles será uma dificuldade ao chegarem ao 9º ano quando irão estudar, por exemplo, razões, escalas e porcentagens. O problema traz também consequências para o Ensino Médio.

Corroborando Bertoni (2009) e Pereira (2009), a maioria dos alunos do Ensino Fundamental sai desse nível de ensino sem dominar as operações básicas com as frações e isso se torna um problema ao chegarem aos anos escolares posteriores, quando precisarão trabalhar com outros ramos da Matemática, como Estatística, Probabilidade, Matemática Financeira, entre outros.

Para tentar minimizar essa dificuldade de aprendizado, apresentamos neste trabalho uma proposta de integração entre a Matemática e a Música explorando os conceitos de razão e proporção existentes nos sons de uma escala musical. É uma proposta prática de aplicabilidade dos conceitos de fração no estudo da teoria musical e na construção de instrumentos, por meio de uma atividade pedagógica interdisciplinar.

De acordo com a Base Nacional Comum Curricular (Brasil, 2017),

a Matemática não se restringe apenas à quantificação de fenômenos determinísticos – contagem, medição de objetos, grandezas – e às técnicas de cálculo com os números e com as grandezas, pois também estuda a incerteza proveniente de fenômenos de caráter aleatório. A Matemática cria sistemas abstratos que organizam e inter-relacionam fenômenos do espaço, do movimento, das formas e dos números, associados ou não a fenômenos do mundo físico. Estes sistemas contêm ideias e objetos que são fundamentais para a compreensão de fenômenos, a construção de representações significativas e argumentações consistentes nos mais variados contextos (Brasil, 2017, p. 265).

Assim, percebe-se que a Matemática transcende à quantificação de fenômenos determinísticos e as técnicas de cálculo. Ela se aplica à compreensão de fenômenos, à construção de representações e às argumentações consistentes em diversos contextos da vida e do conhecimento humano.

Este artigo é parte da dissertação de conclusão do mestrado Profmat (PUC/Rio) que se encontra em fase de elaboração pelos mesmos autores.

A interdisciplinaridade como abordagem pedagógica

Segundo Paulo Freire (1996), a interdisciplinaridade deve ser pensada como um processo contínuo e inacabado de construção do conhecimento, permitindo que os professores trabalhem assuntos reais a fim de que os alunos possam discutir, analisar, questionar e verificar a veracidade dos fatos. Essa integração entre áreas do conhecimento ainda possibilita desenvolver a curiosidade dos estudantes e a realidade com os conteúdos, superando as dificuldades no processo de ensino-aprendizagem.

A interdisciplinaridade é uma abordagem pedagógica que busca integrar conhecimentos de diferentes disciplinas, promovendo uma aprendizagem mais significativa e contextualizada. No ensino de razão e proporção, a interdisciplinaridade entre a Matemática e a Música pode ser explorada mediante as relações existentes entre as diferentes frequências do som. Essa abordagem apresenta como vantagem a contextualização, pois ao utilizar a música como elemento de estudo os alunos podem compreender melhor os conceitos do tema.

O estudo dos fenômenos físicos, como as frequências das diversas notas musicais, também são fascinantes e despertam a curiosidade do educando e o seu interesse pela Matemática como uma ferramenta para entendê-los. A aplicação da Matemática para explicar e entender as frequências sonoras geradas pelos instrumentos musicais dão sentido ao seu estudo, que é fundamental para o avanço do conhecimento científico. Assim, as disciplinas se complementam e se beneficiam mutuamente, proporcionando uma compreensão mais profunda e precisa das três áreas de conhecimento.

Vale ressaltar que a música é uma forma de expressão cultural muito presente no cotidiano das pessoas. Ao trazê-la para a sala de aula, os alunos se sentem mais motivados e engajados com o tema, o que facilita a aprendizagem.

Observa-se, assim, que a interdisciplinaridade possibilita diversas conexões entre diferentes áreas do conhecimento, contribuindo para uma aprendizagem mais autônoma, crítica e duradoura. Incentivar o estudo de tópicos matemáticos com a música pode propiciar aos alunos uma melhor compreensão dos saberes envolvidos e uma visão mais globalizada das interseções e das transferências que podem ser realizadas inclusive com outras áreas do conhecimento.

Dessa forma, a utilização de metodologias diferenciadas com sentido lúdico estimula o aprendizado e contribui para a construção da autonomia acadêmica dos educandos. Essas metodologias de ensino colaboram para que o aluno adquira confiança em seu potencial, tornando-o protagonista do seu aprendizado (Pereira; Santos; Cruz, 2023). Segundo Thiesen (2008),

o que se pode afirmar no campo conceitual é que a interdisciplinaridade será sempre uma reação alternativa à abordagem disciplinar normalizadora (seja no ensino ou na pesquisa) dos diversos objetos de estudo. Independente da definição que cada autor assuma, a interdisciplinaridade está sempre situada no campo onde se pensa a possibilidade de superar a fragmentação das ciências e dos conhecimentos produzidos por elas e onde simultaneamente se exprime a resistência sobre um saber parcelado (Thiesen, 2008, p. 567).

Os ganhos da interdisciplinaridade são visíveis em relação à abordagem tradicional de ensino, pois permitem uma integração de saberes por meio de uma visão ampla do conhecimento, algo mais coerente e viável à aprendizagem do indivíduo.

A Música e os conceitos matemáticos

A relação entre Música e Matemática é profunda e fascinante. A primeira, em grande parte, é uma manifestação organizada de sons e ritmos e a segunda fornece a estrutura subjacente que permite essa organização. Segundo Stewart (2012), a Música é uma forma de arte e está intrinsecamente ligada à Matemática. Na arte musical, as relações matemáticas são utilizadas para criar harmonias, melodias e ritmos agradáveis ao ouvido humano.

Segundo Med (1996), três das principais maneiras pelas quais a Música e a Matemática estão relacionadas são:

1. Ritmo: é uma parte fundamental da música. A duração – das notas, das pausas e das batidas – é organizada em padrões rítmicos. A Matemática dos compassos musicais é um estudo que busca compreender a relação entre os tempos e os compassos da música, utilizando conceitos matemáticos para organizar e medir essas estruturas. De acordo com Med (1996), a fórmula de compasso é definida por uma fração na qual o numerador define a quantidade de notas e, o denominador, o tipo de nota de cada compasso. O compasso é a organização básica do ritmo na música e é composto por uma determinada quantidade de tempos. Cada tempo é uma unidade de duração que pode ser subdividida em partes menores, como semínimas, colcheias etc. A organização dos compassos e dos tempos é fundamental para a interpretação e execução correta de uma peça musical. A matemática dos compassos musicais envolve diversos conceitos, como frações, proporções e sequências. Por exemplo, o compasso 4/4, também chamado de quaternário, é um dos mais comuns na música ocidental e indica que cada compasso é composto por quatro tempos, ou seja, para preenchê-lo precisamos de quatro notas com duração de um tempo. Observamos que o desenho da duração do tempo das notas musicais segue uma progressão geométrica com razão 1/2 e o primeiro termo é igual a 4. A Tabela 1 mostra a distribuição das notas num compasso quaternário. Nesse caso, a Matemática é utilizada para medir e organizar os tempos dentro de um compasso.

Tabela 1: Duração do tempo de execução das notas musicais

2. Harmonia e acordes: uma nota musical é uma frequência de som que ouvimos pela propagação de uma onda pelo ar. A escala atual possui sete notas e doze sons. O símbolo # (sustenido) ou b (bemol) adicionado à esquerda da nota representa um deslocamento de um semitom para cima ou para baixo, respectivamente. As frequências das notas entre DÓ4 e DÓ5 estão na Tabela 2.

Tabela 2: Frequência em Hz das notas musicais entre DÓ4 e DÓ5

A melodia é uma combinação de sons de diferentes frequências, ritmos e altura dos sons (graves ou agudos). O resultado dessa sequência de frequências e ritmos chamamos de desenho melódico ou melodia (Med, 1996). A harmonia na música envolve a combinação de diferentes notas para criar acordes e progressões harmônicas.

De acordo com Guest (2020), o intervalo musical é a distância entre as notas (ou entre frequência de sons). Esses intervalos são nomeados de acordo com a quantidade de tons e semitons existentes entre eles, quando um tom equivale a dois semitons, conforme exemplificado na Tabela 3.

Tabela 3: Exemplificação de intervalos musicais

Os acordes são sons obtidos quando tocamos mais de uma nota musical simultaneamente. Eles são capazes de transmitir sensações diferentes ao ouvido humano. A Matemática é fundamental para se desenvolver musicalmente e está muito presente nos acordes e na harmonia. Vamos exemplificar um acorde composto por três sons, ou seja, três notas musicais, no qual, a partir da nota mais grave para a mais aguda, as notas estão separadas por intervalos de cinco semitons e quatro semitons. Essa sequência forma um acorde que chamamos de tríade (três sons) maior ou, simplesmente, um acorde maior.

3. Escalas musicais: Existe uma lenda de que Pitágoras (569 a.C.-480 a.C., aproximadamente) despertou sua curiosidade em relação à música quando, ao passar em frente à oficina de um ferreiro, ouviu o som de martelos batendo em uma bigorna e percebeu que os martelos soavam harmonicamente, exceto um. Curioso, ele estabeleceu uma relação entre os martelos que eram harmônicos e percebeu que a massa de cada martelo era de 12, 9, 8 e 6 unidades de peso.

Abdounur (2006) relata os experimentos de Pitágoras. Ele observou que os números que representam as massas dos martelos, ou seja, 6, 8, 9 e 12, formam as proporções 6/8 = 9/12 e 6/9 = 8/12. Além disso, 9 é a média aritmética entre 6 e 12 e 8, a média harmônica de 6 e 12. Pitágoras também experimentou as proporções entre os pesos 6=1/2×12; 8=2/3×12 e 9=3/4×12 e descobriu que os intervalos musicais proporcionais aos números 1/2; 2/3 e 3/4 eram agradáveis ao ouvido humano.

Tabela 4: Razão das frequências da escala de Pitágoras

Pitágoras dividiu a escala de maneira que a cada nota uma fração fosse associada, como pode ser visualizado na Tabela 4. Atualmente, a escala temperada criada por Bach – compositor, cantor, maestro, professor, organista, cravista, violista e violinista da Alemanha mundialmente conhecido – é uma escala musical que divide a oitava em 12 semitons de igual tamanho, não por meio de frações, como fez Pitágoras, mas por logaritmos.A escala foi desenvolvida para permitir que a música seja tocada em diferentes tonalidades sem a necessidade de ajuste da afinação dos instrumentos. É amplamente utilizada atualmente e é considerada o padrão de afinação na música ocidental.

Música e Matemática

Como a razão entre as frequências de duas notas do intervalo e de uma oitava é igual a 2 (observado na Tabela 2), o intervalo entre uma oitava possui 12 semitons (distribuição da escala temperada de Bach). Assim, podemos escrever as frequências das notas musicais como uma progressão geométrica conforme abaixo:

Considerando 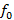 , a frequência do primeiro grau da escala e r razão entre duas frequências consecutivas. Então,

⇔

 ,

,

…

 ,

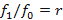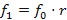
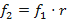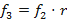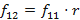e multiplicando os lados das equações, obtemos

. . . . . . . . . . . = . . . . . . . . . . . .

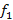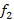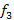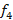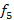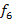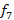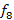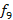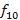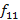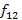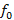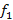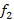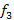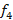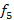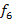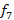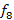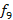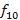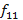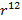
Simplificando os fatores comuns aos dois membros das equações, concluímos que 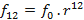. Além disso, como 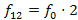(notas musicais com intervalo de uma oitava), temos que 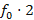=  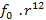, ou seja, .

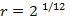Assim, as frequências de uma escala musical seguem uma progressão geométrica, na qual a razão 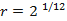 . Com isso, podemos definir a frequência de uma nota como uma função do tipo

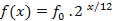(Equação 1),

em que x é a quantidade de semitons existentes entre a nota que se deseja encontrar a frequência e a nota padrão com frequência 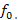 Note que x pertence ao conjunto dos números inteiros.

Em 1936, uma conferência internacional recomendou que o LÁ4, LÁ, que pertence à 4ª oitava do piano e se encontra à direita do dó central, fosse afinado na frequência igual a 440 Hz. Esse padrão foi adotado pela Organização Internacional para Padronização em 1955, como a norma ISO 16. Desde então, essa é a frequência de referência para a afinação de todos os instrumentos musicais.

Partindo da nota padrão LÁ4 com frequência 440 Hz, encontramos as frequências das notas que compõem o intervalo de uma oitava. Na tabela 2, foram calculadas as frequências da oitava DÓ4 a DÓ5 partindo da frequência do LÁ4 e considerando a razão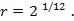

Música e Física

O estudo dos tubos sonoros faz parte da acústica, um dos ramos da Física. Esse ramo permite saber qual o comprimento e o diâmetro dos tubos necessários para produzir uma determinada frequência, gerando uma nota musical. Os tubos de PVC abertos ressoam em frequências bem definidas dependendo do seu comprimento e o som é emitido ao gerar a onda sonora da percussão na extremidade do tubo.

Abdounur (2006) declara que

tanto uma corda como coluna de ar em instrumentos de sopro possuem a característica de vibrar não apenas como um todo, mas ainda simultaneamente como duas metades, três terços, quatro quartos etc. Do ponto de vista matemático, observa-se que a força de cada harmônico contribuirá para a construção da forma da vibração periódica que, por sua vez, relaciona-se com o timbre do som (Abdounur, 2006, p. 91).

Dessa forma, a onda sonora gerada em um tubo tem a frequência calculada pelas equações:

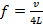(1) para tubos com uma extremidade fechada;

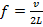(2) para tubos abertos,

em que a velocidade (v) da onda no tubo é aproximadamente igual a 342 m/s.

Partindo de (1), o comprimento do tubo fica, então, definido da seguinte forma:

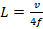(Equação 2)

Para se obter a frequência com o rigor das medidas de frequências obtidas por um osciloscópio, devemos “corrigir” subtraindo os comprimentos obtidos por 1/4 do diâmetro interno do tubo. Logo, a fórmula para encontrar o comprimento do tubo com correção:

)

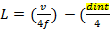A Tabela 2 mostra a frequência encontrada dos 12 semitons da escala a partir da frequência do LÁ4, em destaque as sete notas naturais.

Influência da Matemática na construção de instrumentos

Na atividade de construção de instrumentos musicais, os alunos podem realizar pesquisas de como a razão e a proporção são utilizadas nesse processo. Dessa forma, a atividade envolve a investigação a respeito da aplicação desses conceitos na confecção de instrumentos musicais. Isso permite que os estudantes compreendam a importância da Matemática na Música e na construção de instrumentos, como:

1. Comprimento das cordas: o comprimento das cordas dos instrumentos de corda, como violão e violino, afeta a altura das notas produzidas. A relação entre o comprimento da corda e a frequência da nota é inversamente proporcional. Por exemplo, se uma corda é dividida ao meio, a frequência da nota produzida será o dobro da frequência original. Quanto menor for o comprimento da corda, maior será a frequência do som emitido, ou seja, mais agudo será o som. Esse mesmo raciocínio se aplica ao tamanho dos tubos na confecção de instrumentos com tubos.
2. Tambores e instrumentos de percussão: o tamanho e as proporções dos tambores e de outros instrumentos de percussão também influenciam no som que é produzido. Por exemplo, o tamanho e o diâmetro do tambor afetam a ressonância e a frequência das notas produzidas quando ele é tocado.
3. Afinação dos instrumentos: a afinação dos instrumentos musicais é realizada por meio de ajustes das proporções entre as notas em relação a um padrão de referência, como o LÁ4.

Percursos metodológicos

Na busca de integrar as disciplinas Matemática, Música e Física, realizamos quatro encontros com duração de 50 minutos cada com alunos da turma do 8° ano do Ensino Fundamental de uma escola municipal do Rio de Janeiro. Participaram da atividade dez alunos voluntários, com idades entre 13 e 15 anos. Os encontros foram realizados em sala de aula e no auditório da escola durante o mês de outubro de 2023.

1º dia de oficina

No primeiro encontro, fizemos uma breve introdução a respeito das relações entre Matemática e Música. Em sala de aula, utilizando slides, apresentamos o experimento de Pitágoras com o desenho do monocórdio, demonstrando aos alunos como Pitágoras encontrou as frações que representam os intervalos entre as notas musicais na escala pitagórica. Durante este encontro, os alunos fizeram várias operações de adição e subtração com frações, reproduzindo os cálculos do experimento de Pitágoras. Os alunos ficaram muito curiosos e fascinados com a relação entre as frações e o som da escala musical. Nessas atividades exploramos as habilidades EF06MA08, EF06MA09, EF06MA10, EF06MA11 e EF69AR21 da BNCC (Brasil, 2017).

2º dia de oficina

O segundo encontro aconteceu no auditório da escola e os alunos assistiram ao filme Donald no país da Matemágica (Disney, 1959). Esse filme, além de mostrar a relação entre Música e Matemática, também traz muitas curiosidades da Geometria e a relação da Matemática com os jogos.

Após o filme, houve uma roda de discussão a respeito da presença da Matemática em diversas áreas do conhecimento. Falamos da possibilidade de aplicar conhecimentos matemáticos para desenvolver um instrumento e os alunos ficaram bastante motivados. Como os educandos não conheciam a teoria musical, foi necessário o planejamento de algumas explicações do tema, como os conceitos de escala e de intervalo. Nesse momento, foi enriquecedora a presença de um professor de Arte, com unidade temática em Música, explorando a habilidade EF15AR16 contida na BNCC (Brasil, 2017). A partir disso, decidimos que faríamos um instrumento utilizando tubos de PVC. Por fim, registramos as definições feitas pelo grupo e encerramos o encontro.

3º dia de oficina

Começamos a aula com os conceitos necessários de teoria musical e decidimos que nosso instrumento teria uma oitava na escala de dó Maior, por serem apenas de notas naturais. Assim, a partir da frequência padrão 440 Hz da nota LÁ4, utilizamos a equação 1 e encontramos a frequência da nota DÓ4, por meio da fórmula:

Frequência (DÓ4) = Frequência (LÁ4) x  ,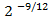

pois entre a nota LÁ4 e a nota DÓ4 existem nove semitons descendentes. Nesse momento, usamos a reta numérica para mostrar a distância de cada nota a partir do LÁ4.

Tabela 5: Memória de cálculo da construção do tubofone

A Tabela 5 possui, na primeira linha, o nome das notas e, na terceira linha, uma reta numérica que será usada para substituir o numerador do expoente, que representa a quantidade de semitons entre cada nota desejada e a nota padrão LÁ4-440. A partir da frequência encontrada na nota dó (261,63), cada aluno calculou a frequência do semitom superior multiplicando a frequência anterior por 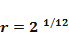, na qual utilizamos 1,05946 (encontrado na calculadora). As frequências encontradas foram registradas na segunda linha da Tabela 5. Com isso, falamos sobre sequência numérica, razão, potência com expoente fracionário, positivo e negativo, operações com números decimais e critérios de arredondamento. Foram exploradas as habilidades EF07MA03, EF07MA04, EF07MA05, EF07MA08, EF07MA09, EF08MA02, EF08MA02 e EF06MA11 da BNCC (Brasil, 2017).

A quarta linha da Tabela 5 foi preenchida com o comprimento do tubo necessário para emitir as frequências dos doze semitons existentes na escala musical de DÓ4 até DÓ5. Nesse momento, utilizamos a Equação 2 para esse cálculo. Com a escolha de construir apenas as notas naturais, as oito frequências das notas naturais foram destacadas. Registramos, na quarta linha da Tabela 5, o comprimento dos tubos necessários para emitir as notas desejadas.

A quinta linha da Tabela 5 foi preenchida com o comprimento calculado para o tubo após aplicação do ajuste. Essa regulagem foi necessária devido a alguns fatores, tais como: imprecisão do método, encaixes de peças com joelhos de 90 graus, cortes de tubos feitos manualmente, com serra e velocidade arbitrada em 342 m/s.

Nesse dia, foram exploradas as habilidades EF07MA04, EF07MA11, EF07MA12, EF09MA03, EF15AR14 e EF15AR15 da BNCC (Brasil, 2017).

4º dia de oficina

Para esse encontro, foi necessária a obtenção do material projetado no encontro anterior: 3m de tubo com 4cm de diâmetro, joelhos de 90 graus, serra para cortar o tubo, lixa para acabamento e ajuste. Como são crianças do 8°ano, para evitar algum acidente com os cortes do tubo, levamos para o momento os tubos já serrados nas medidas encontradas no 3º encontro na planilha de projeto, registradas na quarta linha da Tabela 5.

Montamos os tubos e testamos a afinação, utilizando o app no celular Turner T1 (software gratuito que indica a frequência do som emitido pelo tubo). Com a imprecisão dos cortes manuais dos canos e de encaixes de joelhos de 90 graus, alguns tubos não mediram as frequências exatas, sendo necessário um ajuste com a lixa até chegar à frequência desejada. O tubofone ficou afinado e conseguimos tocar algumas músicas simples, porém os canos não estavam fixados numa estrutura. Tivemos a ideia de adaptar uma peça de curva 90° para facilitar a execução nos tubos deitados sobre a mesa e uma peça que serviria como junção dividindo os canos em duas partes. Os alunos ficaram muito felizes e realizados por participarem da construção do instrumento. Com as adaptações, o tubofone ficou mais didático para trabalhar em sala de aula, pois pode ser apoiado na mesa do aluno (Figura 3). Nesse dia, foram exploradas as habilidades EF69AR06, EF69AR08, EF69AR20 e EF69AR22 da BNCC (Brasil, 2017).

Considerações finais

Este artigo é uma tentativa de mostrar que o uso de recursos didáticos adequados ao conteúdo permite aprimorar e diversificar a forma de ensino-aprendizagem. Adicionalmente, também permite ampliar as relações entre o professor e o estudante, estimulando a integração em favor da capacidade de abstração do educando, contribuindo para a sua evolução em diferentes áreas do conhecimento.

A Música, uma das principais formas de expressão cultural e de significativa presença no cotidiano dos adolescentes, motiva, engaja e dá significância aos conteúdos a serem transmitidos, facilitando a aprendizagem.

A interdisciplinaridade com a Matemática mostra que as disciplinas se complementam e se beneficiam mutuamente, proporcionando uma poderosa ferramenta ao professor e uma compreensão mais profunda e real aos alunos a respeito dos conceitos matemáticos.

Ao final da pesquisa, pode-se entender que a integração entre os conceitos da Matemática aplicados à Música podem ser uma oportunidade de ensino-aprendizagem com uma abordagem metodológica integrativa, em especial para os alunos que apresentam afinidade com a Música.

O presente trabalho foi realizado com o apoio da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Capes), código de financiamento 001.

Referências

ABDOUNUR, O. J. Matemática e música: pensamento analógico na construção de significados. São Paulo: Escrituras, 2006.

BERTONI, N. E. Educação e linguagem matemática. Brasília: Editora da Universidade de Brasília, 2009.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília: MEC, 2017. Disponível em: http://basenacionalcomum.mec.gov.br/documentos/bncc-2versao.revista.pdf. Acesso em: 29 ago. 2023.

DANTAS, J. D.; CRUZ, S. DA S. Um olhar físico sobre a teoria musical. Revista Brasileira de Ensino de Física, v. 41, n° 1, 2019. Disponível em: https://doi.org/10.1590/1806-9126-RBEF-2018-0099. Acesso em: 29 ago. 2023.

DISNEY, Walt. Donald no país da Matemágica. Diretor: Hamilton Luske. Produtor: Walt Disney. Hollywood: Walt Disney Productions, 1959. 27 min. Filme.

FREIRE, P. Pedagogia da Autonomia: saberes necessários à prática educativa. 25ª ed. São Paulo: Paz e Terra, 1996.

GUEST, Ian. Harmonia: método prático. São Paulo: Lumiar, 2020.

MED, Bohumil. Teoria da música. Brasília: Musimed,1996.

PEREIRA, G. M.; MOURA, S.; ORIOSVALDO, M. Avaliação do processo de ensino e aprendizagem em Matemática: contribuições da teoria histórico-cultural. Boletim de Educação Matemática, Rio Claro, v. 22, n° 33, p. 97-116, 2009. Disponível em: https://www.periodicos.rc.biblioteca.unesp.br/index.php/bolema/article/view/2960. Acesso em: 29 ago. 2023.

PEREIRA, G. M.; SANTOS, A. S.; CRUZ, J. M. F. S. Aplicação de metodologias diferenciadas no ensino de Ciências, Matemática e Química: da Educação Básica ao Ensino Superior. Revista Educação Pública, Rio de Janeiro, v. 23, n° 15, 25 de abril de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/23/15/aplicacao-de-metodologias-diferenciadas-no-ensino-de-ciencias-matematica-e-quimica-da-educacao-basica-ao-ensino-superior. Acesso em: Acesso em: 29 ago. 2023.

SILVA, Domiciano Corrêa Marques. Tubos sonoros. Mundo Educação. Disponível em: https://mundoeducacao.uol.com.br/fisica/tubos-sonoros.htm. Acesso em: 13 nov. 2023.

STEWART, I. Uma história da simetria na Matemática. Rio de Janeiro: ‏Zahar, 2012.

THIESEN J. S. A interdisciplinaridade como um movimento articulador no processo ensino-aprendizagem. Revista Brasileira de Educação, v. 13, n° 39, p. 545-598, set./dez. 2008. Disponível em: https://doi.org/10.1590/S1413-24782008000300010. Acesso em: 29 ago. 2023.