Do pomar às funções: uma abordagem matemática aberta e colaborativa no Ensino Médio
Maristela Santos Aguiar de Souza
Mestra em Educação (Unitau), especialista em Gestão Educacional (Unicsul), licenciada em Matemática (Unitau), professora do Ensino Médio na rede estadual de ensino de São Paulo e Anos Finais do Ensino Fundamental da rede municipal de São Luiz do Paraitinga/SP
Kátia Celina da Silva Richetto
Doutora em Engenharia de Materiais (EEL/USP), mestra em Engenharia Mecânica (Unesp – Guaratinguetá), especialista em Educação a Distância, graduada na Escola de Engenharia (EEL/USP – Lorena), professora titular da Unitau, com pesquisas na linha Práticas Pedagógicas para a Equidade
Willian José Ferreira
Doutor em Geofísica Espacial (Inpe), mestre em Ciências Ambientais (Unitau), licenciado em Física (Unesp), professor do Instituto Básico de Exatas da Unitau, docente do Mestrado Profissional em Educação da Unitau, com pesquisas na linha Práticas Pedagógicas para a Equidade
Somando vozes: colaboração, problemas abertos e equidade em Matemática
A dificuldade em engajar os estudantes nas aulas de Matemática tem levado educadores a buscar práticas pedagógicas inovadoras, entre as quais a aprendizagem colaborativa se destaca como uma estratégia promissora. De acordo com Santos e Souza (2024), a aprendizagem deve ser compreendida como um processo contínuo de reflexão, no qual a colaboração e a cooperação favorecem tanto a autonomia quanto o engajamento ativo dos estudantes.
Nesse contexto, o Programa de Especialização Docente (PED Brasil) regulamenta a organização do trabalho em grupo por meio da atribuição de papéis específicos aos integrantes, como facilitador, harmonizador, repórter, controlador do tempo e monitor de recursos, com o objetivo de assegurar a participação equitativa de todos (Canoa, 2025). Essa estrutura busca promover a equidade educacional ao desenvolver atividades que integram habilidades como criatividade, competências socioemocionais e raciocínio lógico, fortalecendo, assim, o processo de aprendizagem.
Nessa mesma direção, Cohen e Lotan (2017) ressaltam que a aprendizagem colaborativa potencializa o desenvolvimento de habilidades cognitivas complexas, como a formulação de hipóteses e a análise de padrões, aspectos considerados centrais nos currículos contemporâneos e em propostas de atividades desafiadoras desenvolvidas em grupo.
A Matemática, quando abordada de forma significativa, permite que os estudantes compreendam sua relevância. Para atingir esse objetivo, é essencial promover atividades de resolução de problemas que apresentem múltiplas soluções, incentivando o uso diversificado de habilidades intelectuais e estimulando o potencial dos alunos. Boaler (2018) reforça que a matemática é uma disciplina rica em ideias e conexões, capaz de inspirar os estudantes ao promover uma experiência de aprendizado mais profunda e interativa.
Foi desenvolvida uma atividade estruturada como um problema aberto, com múltiplas possibilidades de resolução. Esse formato convida os estudantes à reflexão crítica, incentivando-os a aplicar seus conhecimentos sobre sequências e funções, ao mesmo tempo em que promove a integração de diversos tópicos matemáticos. Van de Walle (2009, p. 57) observa que, “quando os alunos se envolvem em tarefas bem elaboradas baseadas na resolução de problemas, com foco nos métodos de solução, o resultado é uma nova compreensão da matemática embutida na tarefa”. Dessa forma, essa abordagem não apenas incentiva o raciocínio lógico como também favorece o desenvolvimento de habilidades investigativas e colaborativas, essenciais para a formação acadêmica dos estudantes.
Além disso, a atividade foi adaptada a partir das ideias de proporcionalidade e interdependência, conceitos essenciais que permeiam diversos conteúdos curriculares e encontram ampla aplicação em situações do cotidiano. Nesse contexto, Machado (2015) destaca que essas ideias são frequentemente retomadas em diferentes abordagens ao longo do estudo de variados temas, criando conexões que tornam a aprendizagem mais significativa e relevante para os alunos. Essas noções, conforme previsto na Base Nacional Comum Curricular (BNCC), são trabalhadas de maneira a promover o desenvolvimento de competências essenciais ao longo do bimestre letivo (Brasil, 2017), fortalecendo o vínculo entre o conteúdo matemático e as experiências práticas dos estudantes.
Em consonância com discussões recentes sobre equidade em aulas de matemática, entendemos que promover participação justa exige reconfigurar rotinas de interação e de avaliação para que os diferentes repertórios culturais dos estudantes tenham valor epistêmico na atividade e não sejam invisibilizados (Ferreira; Richetto, 2025).
À luz dessas referências, apresentamos a seguir o desenho da atividade, seus procedimentos e evidências de aprendizagem dos estudantes.
Explorando funções, padrões e proporcionalidade na Matemática
Relatamos uma experiência pedagógica desenvolvida com uma turma de 30 alunos da segunda série do Ensino Médio em uma Escola Estadual no Vale do Paraíba, São Paulo, utilizando a metodologia do Programa de Especialização Docente (PED Brasil). Os estudantes foram organizados em grupos de cinco integrantes, com funções específicas distribuídas entre os membros, e receberam uma situação-problema adaptada para alinhar-se à habilidade prevista pela BNCC (EM13MAT302), que envolve a resolução e a elaboração de problemas cujos modelos são as funções polinomiais de 1º e 2º graus, em contextos diversos, incluindo ou não tecnologias digitais (Brasil, 2017).
A situação-problema relacionava-se às ideias fundamentais de proporcionalidade e interdependência, explorando o crescimento proporcional entre sequências de macieiras e pinheiros e a inter-relação dessas grandezas. O objetivo central da atividade foi oferecer aos estudantes a oportunidade de explorar padrões e conectá-los ao estudo de funções, promovendo a observação e comparação de diferentes padrões de crescimento, bem como sua representação por meio de figuras, expressões algébricas e gráficas. Além disso, o desenvolvimento do raciocínio lógico-matemático e a promoção da equidade nas interações entre alunos organizados em grupos heterogêneos foram aspectos centrais da proposta.
Segundo Van de Walle (2009), o desenvolvimento do pensamento proporcional é promovido por atividades que envolvem comparações e identificação de padrões, aspectos fundamentais em todas as áreas da matemática. Ele ressalta a importância de ensinar os estudantes a buscar, descrever, traduzir e expandir padrões, habilidades que são essenciais tanto para o raciocínio matemático quanto para o pensamento algébrico. Nessa perspectiva, a análise do crescimento das sequências de macieiras e pinheiros permitiu que os alunos comparassem e identificassem relações proporcionais, ao mesmo tempo em que exploravam diferentes formas de expressar suas respostas, utilizando diversas habilidades cognitivas para aprofundar o aprendizado.
A atividade foi realizada ao longo de duas aulas de 50 minutos cada, totalizando 100 minutos, organizados em três etapas. Na primeira etapa, com duração de 30 minutos, ocorreu a formação dos grupos, a definição das funções de cada integrante, a explanação sobre o desenvolvimento da proposta e a entrega dos materiais. Para favorecer a realização da atividade, cada grupo recebeu um cartão de atividades, além de cartolinas, papéis coloridos, canetas coloridas e papel quadriculado para a confecção dos cartazes.
Na segunda etapa, com duração de 40 minutos, os estudantes desenvolveram a atividade enquanto a professora acompanhava o trabalho em grupo, atuando como mediadora do processo de aprendizagem. Por fim, a terceira etapa, com duração de 30 minutos, foi destinada à socialização das produções, momento em que cada grupo apresentou suas conclusões, finalizando a atividade.
A situação-problema (adaptada de Youcubed, 2020) envolveu o cenário de uma plantação de macieiras, cujo crescimento segue uma sequência de quadrados perfeitos (1, 4, 9, 16), e pinheiros plantados ao redor, cuja progressão baseia-se em múltiplos de oito (8, 16, 24, 32). A proposta permitiu que os estudantes identificassem e comparassem esses padrões, promovendo o reconhecimento de relações proporcionais e o entendimento mais aprofundado de funções. O objetivo principal foi demonstrar a relevância de reconhecer padrões em contextos práticos e aplicar esses conhecimentos na resolução de problemas que envolvem funções e crescimento proporcional. A Figura 1 ilustra os padrões de crescimento, auxiliando na visualização dessas relações e proporcionando uma abordagem mais contextualizada e significativa da Matemática.

Figura 1: Situação-problema
Fonte: Adaptado de https://www.youcubed.org/wp-content/uploads/2020/05/Semana-3-Pomar-de-Macieiras.docx.pdf.
No contexto da equidade educacional na Matemática, essa atividade representa uma abordagem inclusiva que permite a todos os alunos, independentemente de suas habilidades ou experiências prévias, se envolverem no aprendizado de conceitos fundamentais, como padrões e funções. Ao utilizar um cenário prático e acessível, como o crescimento de árvores, a atividade torna os conteúdos mais relevantes e próximos à realidade dos estudantes, conectando a matemática a situações do cotidiano.
A estrutura colaborativa da atividade incentiva a participação de todos, proporcionando um ambiente em que diferentes estilos de aprendizagem e níveis de compreensão se complementam. Isso promove a troca de ideias e a cooperação, garantindo que os estudantes se apoiem no processo de resolução, desenvolvendo habilidades matemáticas de forma coletiva. A proposta, ao integrar situações práticas e promover o diálogo, reforça o aprendizado significativo, ao mesmo tempo em que contribui para a redução das desigualdades educacionais, garantindo que cada estudante tenha oportunidade de desenvolver seu potencial.
Analisando resultados: criatividade e compreensão nas soluções
Os estudantes participaram de forma ativa e produtiva das atividades, engajando-se em discussões dentro de seus grupos. Inicialmente, diferentes estratégias foram empregadas para tentar descobrir a sequência numérica referente ao crescimento das macieiras e dos pinheiros. Alguns grupos focaram na análise das sequências, enquanto outros avançaram para a representação algébrica ou se dedicaram à elaboração de cartazes para apresentar suas conclusões.
As discussões em grupo foram fundamentais para a formulação de respostas coletivas, refletindo o consenso entre os membros. Como produto desse processo colaborativo, cada grupo elaborou um cartaz que sintetizava a solução proposta, a qual será analisada a seguir, considerando tanto os aspectos conceituais abordados quanto a criatividade na apresentação.
O primeiro grupo analisado demonstrou uma compreensão abrangente do problema, identificando corretamente o padrão de crescimento das macieiras e dos pinheiros e reconhecendo o ponto em que as quantidades de ambas se igualam no oitavo pomar, com 64 macieiras e 64 pinheiros, conforme ilustrado na Figura 2.

Figura 2: Cartaz do grupo 1
Essa análise prosseguiu com a consideração de como os demais grupos lidaram com o problema e quais foram as soluções propostas, explorando o uso de diferentes abordagens e estratégias.
O segundo grupo identificou corretamente o ponto de equilíbrio, no qual as quantidades de macieiras e pinheiros se igualam no oitavo pomar, com 64 exemplares de cada árvore, conforme apresentado na Figura 3. Além disso, o grupo desenvolveu uma representação algébrica do problema, porém não forneceu uma demonstração clara dos procedimentos algébricos utilizados para alcançar a solução, também ilustrada na Figura 3.

Figura 3: Cartaz do grupo 2
A escolha de representar o número de macieiras por x² e o número de pinheiros por 8x reflete a habilidade dos estudantes em identificar a natureza das funções envolvidas: uma função quadrática para as macieiras e uma função linear para os pinheiros. Embora o grupo não tenha apresentado uma representação gráfica, essa distinção demonstra uma compreensão algébrica e conceitual das diferentes taxas de crescimento entre as árvores. A associação do crescimento das macieiras a uma função quadrática e dos pinheiros a uma função linear revela uma capacidade de abstração importante, que vai além da mera identificação de padrões numéricos, possibilitando a generalização do problema.
Na sequência, a elaboração de um cartaz criativo para compartilhar suas descobertas reforçou as habilidades de comunicação e de trabalho colaborativo dos estudantes. Ao transmitir suas conclusões de forma visual e acessível, o grupo não só compreendeu o problema, como também conseguiu encontrar formas de comunicar esse entendimento aos colegas, integrando o raciocínio matemático à capacidade de socializar o conhecimento.
Como sugestão de aprofundamento, o grupo poderia explorar representações gráficas das funções envolvidas e investigar como o problema poderia ser resolvido algebricamente de maneira mais detalhada. Ainda assim, o desempenho demonstrado foi positivo, evidenciando uma compreensão avançada dos conceitos e uma abordagem criativa na apresentação dos resultados.
O terceiro grupo, por sua vez, também demonstrou uma compreensão clara do padrão de crescimento das macieiras e dos pinheiros, apresentando a sequência numérica correta e desenvolvendo uma representação algébrica para descrever essas relações, conforme ilustrado na Figura 4.

Figura 4: Cartaz do grupo 3
Ao identificarem a "lei de formação" (Pinheiros = 8n e Macieira = 1 + (n-1) × (n+1)) para ambas as quantidades, eles demonstraram uma habilidade importante de generalização e reconhecimento de padrões numéricos. No entanto, o grupo não conseguiu reconhecer o quadrado perfeito relacionado ao crescimento das macieiras, nem associar essa relação a uma função quadrática, o que indica uma lacuna no entendimento da estrutura algébrica mais profunda do problema. Uma percepção importante foi o Estudante A ressaltar a diferença de crescimento entre as duas sequências:
O número de macieiras aumenta de maneira mais rápida do que o número de pinheiros, por isso mesmo os pinheiros começando com um número maior do que as macieiras eles vão se encontrar no oitavo pomar (Estudante A).
A observação feita pelo Estudante A sobre a diferença de crescimento entre as duas sequências foi relevante, destacando corretamente que o número de macieiras aumenta mais rapidamente do que o de pinheiros, mesmo com o número inicial de pinheiros sendo maior. A previsão de que as duas sequências se encontrariam no oitavo pomar reflete uma tentativa promissora de identificar o ponto de interseção entre os padrões, o que representa um avanço na construção de uma compreensão algébrica. Esse progresso foi confirmado pela sequência numérica representada no cartaz do grupo, que demonstra o crescimento das macieiras e dos pinheiros.
No entanto, o grupo apresentou dificuldades em reconhecer o formato quadrático do crescimento das macieiras, o que impediu uma formulação precisa da função. Uma intervenção pedagógica adequada poderia auxiliar os estudantes a visualizar a relação entre o arranjo das macieiras em forma de quadrado e sua expressão matemática, ajudando-os a associar esse padrão à função quadrática que melhor descreve o crescimento. Ao enfatizar a conexão entre o formato geométrico e sua representação algébrica, os alunos poderiam expandir sua compreensão, reconhecendo com mais clareza como se formam as sequências de crescimento.
O quarto grupo, por sua vez, demonstrou uma compreensão intuitiva sobre o conceito de área e a proporcionalidade entre o número de macieiras e pinheiros. O cartaz produzido foi criativo, incorporando imagens que ajudaram a representar visualmente a resposta, conforme ilustrado na Figura 5. Essa abordagem visual facilitou a comunicação dos conceitos abordados e promoveu uma maior interação entre os membros do grupo.

Figura 5: Cartaz do grupo 4
Os estudantes demonstraram perceber que o número de pinheiros aumenta à medida que mais macieiras são plantadas e a área do pomar se expande, o que revela uma noção de crescimento espacial e de interdependência entre os elementos envolvidos. Essa compreensão é evidenciada na fala da Estudante B:
Cada vez que mais macieiras são plantadas, a área aumenta já os pinheiros são plantados ao redor das macieiras, seu número consequentemente aumenta. [...]
O número de pinheiros não será igual ao de macieiras, pois sempre o número de pinheiros será maior do que o das macieiras (Estudante B).
Embora o grupo tenha identificado corretamente o crescimento no número de árvores, apresentou uma resposta incorreta ao determinar a quantidade exata de macieiras e pinheiros na sequência dos pomares. No pomar 5, por exemplo, indicaram 20 macieiras e 80 pinheiros, o que está em desacordo com o padrão matemático estabelecido. Na tentativa de resolver o problema, o grupo aplicou a regra de três, o que evidencia uma falha na compreensão das diferentes taxas de variação entre as duas sequências.
A análise demonstra que os estudantes ainda não desenvolveram plenamente a habilidade de identificar padrões algébricos ou de formular sequências numéricas claras a partir dessas relações. Embora tenham demonstrado uma compreensão prática da proporcionalidade, conectando o aumento da área ao aumento do número de árvores, carecem de um entendimento mais profundo de como essas quantidades se relacionam matematicamente dentro de uma sequência.
Nesse contexto, é importante destacar que os erros fazem parte do processo de aprendizagem, incentivando uma mentalidade de crescimento nos estudantes. Como Boaler (2018) afirma, "quando a Matemática é ensinada como uma disciplina aberta e criativa, baseada em conexões, aprendizagem e crescimento, e os erros são incentivados, coisas incríveis acontecem". Dessa forma, a análise do erro pode ser uma oportunidade pedagógica para o aprimoramento da compreensão.
Nesse caso, o uso da regra de três diante de taxas não constantes evidenciou um obstáculo conceitual típico de proporcionalidade, que demanda explicitação do modelo adequado (linear × quadrático) e comparação por tabelas/curvas para sustentar a revisão da hipótese do grupo.
Para esse grupo, uma intervenção mais individualizada com foco em padrões e sequências numéricas pode ser extremamente benéfica. Ao abordar de forma mais explícita a estrutura algébrica subjacente ao problema, os estudantes teriam a oportunidade de formalizar melhor a relação entre macieiras e pinheiros, compreendendo os conceitos de interdependência e equivalência nas sequências.
Segundo Munson (2016), o tempo em que os alunos estão envolvidos em atividades práticas pode ocupar uma parte significativa da aula, e saber como utilizar essas interações para promover um ensino responsivo pode ampliar o impacto das práticas pedagógicas dos professores. Nenhum dos grupos realizou uma representação gráfica inicialmente, mas, após a socialização das soluções, foi feita uma intervenção pedagógica para orientar os estudantes a representar a convergência do crescimento das duas árvores em um gráfico no plano cartesiano.
Como parte dessa intervenção, os alunos foram desafiados, em uma atividade de avaliação individual, a resolver a equação algébrica encontrada e construir um gráfico em seus cadernos que ilustrasse a solução proposta, como exemplificado na Figura 6.
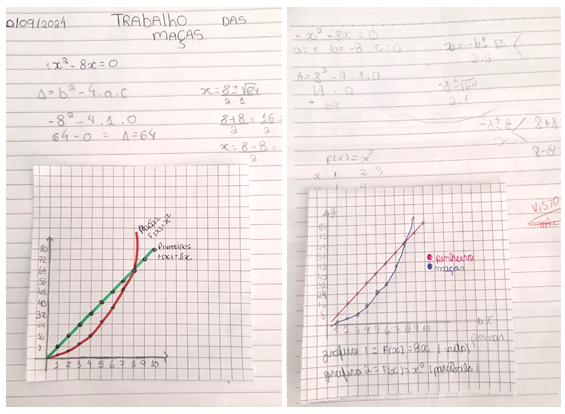
Figura 6: Representação gráfica
A atividade avaliativa mostrou-se bastante exitosa, proporcionando aos alunos uma oportunidade de refletir sobre o trabalho realizado, além de explorar abordagens alternativas para sua resolução. Conforme argumenta Boaler (2018), avaliações bem estruturadas criam momentos significativos de aprendizado. Quando acompanhadas de devolutivas claras, essas atividades contribuem para o desenvolvimento de uma mentalidade de crescimento, incentivando os estudantes a acreditar em sua capacidade de atingir altos níveis de aprendizagem e a compreender os caminhos para alcançar esses objetivos. Esse processo promove uma relação mais consciente e ativa com o próprio aprendizado, possibilitando um avanço significativo na compreensão dos conceitos matemáticos trabalhados.
Considerações finais
A atividade colaborativa atingiu os objetivos de conectar padrões e funções em tarefa aberta, com participação equitativa e múltiplas representações. Os cartazes e as discussões públicas tornaram visíveis as estratégias e os pontos de virada conceitual, sobretudo na distinção entre crescimento linear e quadrático.
Um aspecto de destaque foi o comportamento das sequências, que aumentavam gradualmente e convergiam para um ponto comum, o oitavo pomar, reforçando a compreensão dos conceitos de função. Embora a aula tenha sido positiva, uma análise reflexiva sugere aprimoramentos para futuras aplicações, como a inclusão de mais informações contextuais e uma expectativa mais clara sobre representações algébricas ou gráficas. Esses ajustes podem aprofundar o entendimento dos conceitos matemáticos e aumentar sua aplicabilidade.
Tais aprimoramentos fortaleceriam a atividade, promovendo o desenvolvimento de habilidades matemáticas avançadas e o pensamento crítico. O feedback contínuo e a reflexão sobre o processo de aprendizagem são essenciais para o avanço das competências dos estudantes. Além de facilitar a compreensão dos conceitos, a atividade colaborativa estimulou o interesse dos alunos pela matemática. A continuidade dessa abordagem pode contribuir significativamente para o engajamento e o desenvolvimento das habilidades críticas e criativas dos alunos.
Referências
BOALER, Jo. Mentalidades matemáticas: estimulando o potencial dos estudantes por meio da Matemática criativa, das mensagens inspiradoras e do ensino inovador. Trad. Daniel Bueno, rev. técnica Fernando Amaral Carnaúba, Isabele Veronese e Patricia Cândido. Porto Alegre: Penso, 2018.
BRASIL. Ministério da Educação. Secretaria de Educação Básica. Base Nacional Comum Curricular. Brasília: MEC, 2017.
COHEN, Elisabeth G.; LOTAN, Rachel A. Planejando o trabalho em grupo: estratégias para salas de aula heterogêneas. Trad. Luís Fernando Marques Dorvillé, Mila Molina Carneiro e Paula Márcia Schumaltz Ferreira Rozin; rev. técnica Mila Molina Carneiro e José Ruy Lozano. 3ª ed. Porto Alegre: Penso, 2017.
FERREIRA, Willian José; RICHETTO, Kátia Celina da Silva. Educação em prol da equidade: a adaptação de práticas avaliativas no contexto multicultural do ensino de Matemática. Educar em Revista, Curitiba, v. 41, e93725, 2025. DOI: 10.1590/1984-0411.93725.
INSTITUTO CANOA. O Programa de Especialização Docente (PED Brasil). [S. l.]: Instituto Canoa. Disponível em: https://institutocanoa.org/ped-brasil/. Acesso em: set. 2025.
MACHADO, Nilson José. Sementes 1 # Matemática: ideias fundamentais. São Paulo, 14 out. 2015. Disponível em: https://www.nilsonjosemachado.net/sementes-1-matematica-ideias-fundamentais/. Acesso em: set. 2025.
MUNSON, J. Conferring in the Elementary Mathematics Classroom: A framework. In: NCTM RESEARCH CONFERENCE, 2016, San Francisco, California. [Anais...]. San Francisco, 2016.
SANTOS, Décio Oliveira dos; SOUZA, José Clécio Silva de. Aprendizagem colaborativa e Taxonomia de Bloom em sala de aula. Revista Educação Pública, Rio de Janeiro, v. 24, nº 6, 4 out. 2024. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/24/6/aprendizagem-colaborativa-e-taxonomia-de-bloom-em-sala-de-aula. Acesso em: set. 2025.
VAN DE WALLE, John. Matemática no Ensino Fundamental: formação de professores e aplicações em sala de aula. Trad. Paulo Henrique Colonese. 6ª ed. Porto Alegre: Artmed, 2009.
YOUCUBED. Semana 3 – Pomar de Macieiras. In: YOUCUBED. YouCubed. Stanford: YouCubed, 2020. Disponível em: https://www.youcubed.org/wp-content/uploads/2020/05/Semana-3-Pomar-de-Macieiras.docx.pdf. Acesso em: set. 2025.
Publicado em 19 de novembro de 2025
Como citar este artigo (ABNT)
SOUZA, Maristela Santos Aguiar de; RICHETTO, Kátia Celina da Silva; FERREIRA, Willian José. Do pomar às funções: uma abordagem matemática aberta e colaborativa no Ensino Médio. Revista Educação Pública, Rio de Janeiro, v. 25, nº 44, 19 de novembro de 2025. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/25/44/do-pomar-as-funcoes-uma-abordagem-matematica-aberta-e-colaborativa-no-ensino-medio
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

