Quadriláteros em ação: uma aventura colaborativa nos anos finais do Ensino Fundamental
Samyra Faria Fontes Aljbaae
Mestranda em Educação (Unitau), professora de matemática na rede estadual de São Paulo
Kátia Celina da Silva Richetto
Doutora em Engenharia de Materiais (EEL/USP), mestra em Engenharia Mecânica (Unesp - Guaratinguetá), especialista em Educação a Distância e graduada em Engenharia (EEL/USP), professora titular da Unitau na Graduação, EaD e no Mestrado Profissional em Educação
Willian José Ferreira
Doutor em Geofísica Espacial (INPE), mestre em Ciências Ambientais (Unitau), licenciado em Física (Unesp – Guaratinguetá), professor da Unitau no Instituto Básico de Exatas, nos cursos de Física e Matemática do EaD e no Mestrado Profissional em Educação
O ensino de quadriláteros nos anos finais do Ensino Fundamental é uma oportunidade para fortalecer o conhecimento geométrico dos estudantes, permitindo que compreendam e avaliem formas com base em suas propriedades. Nesse estágio, a Geometria vai além da simples identificação de figuras, envolvendo uma análise mais detalhada dos atributos dos quadriláteros, como os tipos de ângulos, lados congruentes e relações de paralelismo e perpendicularidade. Essa abordagem permite que os alunos desenvolvam habilidades de observação e raciocínio lógico, promovendo uma compreensão mais profunda das relações espaciais e estruturais. Este relato descreve uma experiência com estudantes do 7º ano do Ensino Fundamental de uma escola da rede estadual de São Paulo, na qual foram desenvolvidas atividades colaborativas em grupo.
Além de fornecer uma base para estudos mais aprofundados em Geometria, o estudo dos quadriláteros possibilita que os alunos realizem conexões com situações do cotidiano. Figuras como quadrados, retângulos e trapézios estão presentes em diversos contextos, desde a construção civil até o design de objetos, o que reforça a relevância prática e a aplicabilidade desses conceitos. É fundamental que o ensino de quadriláteros inclua metodologias ativas – como a resolução de problemas e o trabalho em grupo colaborativo – para engajar os estudantes e incentivar a aplicação prática do conteúdo.
A Base Nacional Comum Curricular (BNCC) prevê, entre as habilidades a serem desenvolvidas, a capacidade de identificar e classificar quadriláteros com base em seus lados e ângulos, além de explorar as relações de inclusão e intersecção entre suas classes. Para atingir esses objetivos, é necessário que os professores promovam um ambiente de aprendizagem que valorize a exploração, a colaboração e o pensamento crítico, possibilitando que os alunos não apenas memorizem fórmulas e definições, mas também construam uma compreensão significativa da geometria dos quadriláteros (Brasil, 2017).
Para enriquecer o ensino nos anos finais do Ensino Fundamental, o Programa de Especialização Docente (PED Brasil) tem sido uma referência importante ao propor práticas pedagógicas que promovem a equidade e a aprendizagem colaborativa. Esse programa, desenvolvido em parceria com o Instituto Canoa, visa formar professores capazes de criar ambientes de aprendizagem inclusivos e desafiadores, onde habilidades como raciocínio lógico, colaboração e resolução de problemas são fomentadas (Canoa, 2024).
Nesse contexto, Van de Walle (2009) destaca que o ensino de Geometria deve ir além do reconhecimento de formas. Ele sugere que a compreensão das relações entre os atributos dos quadriláteros, como ângulos e lados, é fundamental para o desenvolvimento do cálculo geométrico dos estudantes. O autor defende que, ao explorar essas propriedades em atividades que promovam a resolução de problemas e o trabalho em grupo, os alunos têm a oportunidade de construir uma base sólida para o entendimento das inter-relações entre diferentes figuras geométricas. Segundo ele, essa abordagem promove um aprendizado mais ativo e significativo, uma vez que incentiva a análise crítica e a formulação de hipóteses.
O presente relato tem como objetivo principal investigar e implementar práticas pedagógicas colaborativas que promovam a equidade e a resolução de problemas, com o intuito de desenvolver uma compreensão significativa das propriedades geométricas entre os estudantes.
Um aspecto central dessa experiência é a questão: de que maneira as práticas pedagógicas podem favorecer a compreensão e a classificação de quadriláteros pelos alunos dos anos finais do Ensino Fundamental, levando em conta as diversas habilidades e os contextos sociais? Essa indagação é primordial, pois um ambiente escolar inclusivo deve proporcionar a todos os alunos a chance de se envolver no processo de aprendizagem.
Apesar da relevância desse tema, percebemos uma lacuna na literatura sobre a integração específica de metodologias ativas e colaborativas no ensino de quadriláteros. Essa ausência de estudos que abordem essa intersecção pode limitar a eficácia das práticas pedagógicas na promoção de um aprendizado significativo e inclusivo. Este relato visa não apenas preencher essa lacuna, mas também contribuir para a formação de professores capacitados a criar ambientes que estimulem o raciocínio lógico, a colaboração e a resolução de problemas.
Ao conectar o objetivo da nossa experiência com as questões levantadas e as lacunas identificadas, buscamos enriquecer o ensino da Geometria no Ensino Fundamental. Nossa abordagem valoriza a exploração, a colaboração e o pensamento crítico, proporcionando aos alunos uma compreensão mais profunda das relações espaciais e estruturais presentes nas figuras geométricas.
Explorando quadriláteros
O relato descreve a aplicação de uma atividade de classificação de quadriláteros em uma turma de 7º ano do Ensino Fundamental de uma escola estadual do Programa de Ensino Integral (PEI) do Vale do Paraíba paulista. A atividade fez parte do planejamento reverso de uma unidade de Geometria que abrangeu os temas de triângulos, quadriláteros, plano cartesiano e simetria elaborado com base nas habilidades previstas na BNCC e no material didático digital do Centro de Mídias de São Paulo (CMSP) (São Paulo, 2024).
O planejamento reverso, conforme proposto por Wiggins e McTighe (2019), é uma abordagem pedagógica que orienta os professores a planejar a aula a partir dos objetivos de aprendizagem que desejamos alcançar. Esse modelo se concentra inicialmente nos resultados esperados, definindo o que os alunos devem compreender e ser capazes de fazer ao final da unidade.
No planejamento da unidade, o trabalho em grupo desempenhou papel central, conforme os princípios de Cohen e Lotan (2017) sobre aprendizagem colaborativa. As autoras enfatizam a importância do trabalho em grupo intencionalmente estruturado, em que os alunos são incentivados a colaborar, compartilhar conhecimentos e apoiar o aprendizado mútuo em ambientes heterogêneos.
Metodologia
A atividade foi desenvolvida em duas aulas de Matemática seguidas, totalizando 1h30min. Os estudantes foram organizados em grupos de quatro membros, sorteados aleatoriamente, com atribuição de papéis. Cohen e Lotan (2017) destacam que a formação de grupos heterogêneos é essencial para combater desigualdades de status entre os alunos, oferecendo oportunidades de interação e colaboração com colegas com diferentes habilidades, o que promove uma experiência de aprendizado mais inclusiva. Além disso, os autores enfatizam a importância da atribuição de funções dentro dos grupos. A definição de funções específicas para cada membro – como facilitador, repórter, harmonizador, monitor de recursos e controlador do tempo – garante a participação ativa e a responsabilidade de todos.
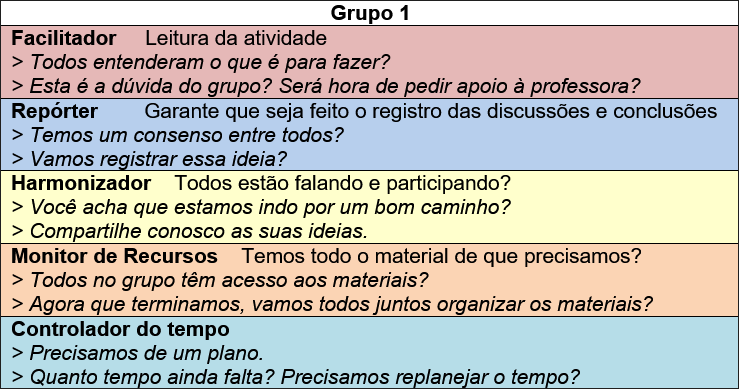
Figura 1: Cartão de papéis dos membros dos grupos
Fonte: Adaptado de Cohen e Lotan (2017, p. 112).
A escolha dos grupos e a atribuição de papéis ajudaram a criar um ambiente de equidade, onde cada aluno pudesse se envolver de forma significativa e explorar suas capacidades. Para o desenvolvimento da atividade, foi elaborado um cartão de recursos, que incluiu uma síntese do material didático estudado anteriormente e apresentou os principais pontos abordados sobre quadriláteros.

Figura 2: Cartão de recursos sobre quadriláteros
Fonte: Aulas 25 a 28 do material digital do CMSP, 7º ano, 3º bimestre.
Para a dinâmica do trabalho em grupo, foi planejado um cartão de atividades. A tarefa consistia em construir modelos de quadriláteros que representassem características específicas. Cohen e Lotan (2017) defendem que as atividades de trabalho em grupo devem ser cuidadosamente estruturadas para fomentar uma participação ativa e igualitária entre todos os estudantes. Os autores afirmam que essas atividades devem ser suficientemente complexas e desafiadoras para promover a interdependência positiva, em que cada aluno precisa colaborar para alcançar o objetivo coletivo.
Jo Boaler (2018) complementa essa visão ao afirmar que as atividades matemáticas devem ser criativas e estimular o pensamento crítico dos estudantes, promovendo uma aprendizagem rica e significativa. Ela ressalta a importância de encorajar os alunos a explorar ideias e fazer conexões, afirmando que a Matemática deve ser vista como uma disciplina aberta e criativa, em que os erros são oportunidades de crescimento e a compreensão se aprofunda por meio de atividades que envolvem desafios e trabalho em conjunto. Nesse contexto, foi proposta uma atividade em que os estudantes deveriam discutir sobre os quadriláteros com base em seus conhecimentos prévios, utilizando papel quadriculado, régua e outros materiais para desenhar suas compreensões.

Figura 3: Cartão de atividade sobre quadriláteros
Resultados e análise das produções dos estudantes
Durante a atividade, enquanto os estudantes desenvolviam suas produções em grupo, a autora circulava pela sala mediando as interações e observando como cada grupo aplicava os conceitos de forma única. Cohen e Lotan (2017) destacam que o papel do professor é essencial para apoiar e monitorar as interações, garantindo que todos os alunos estejam engajados e que a dinâmica do grupo seja equilibrada. Dessa forma, as atividades em grupo promovem não apenas o aprendizado acadêmico como também desenvolvem habilidades de comunicação, resolução de problemas e cooperação, fundamentais para construir uma sala de aula inclusiva e colaborativa.
Entre os nove grupos formados durante a aula, três produções foram selecionadas para análise: as dos grupos 1, 3 e 7.
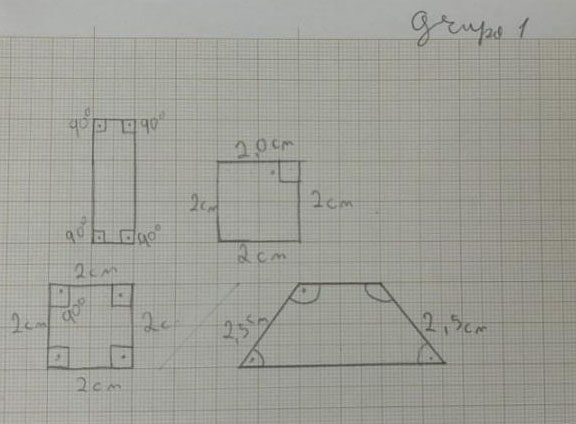
Figura 4: Produção do Grupo 1
O grupo 1 enfrentou dificuldades para completar o desenho de todos os quadriláteros e não rotulou as figuras conforme as instruções. No entanto, indicou ângulos retos e lados iguais, revelando um entendimento parcial das características geométricas.
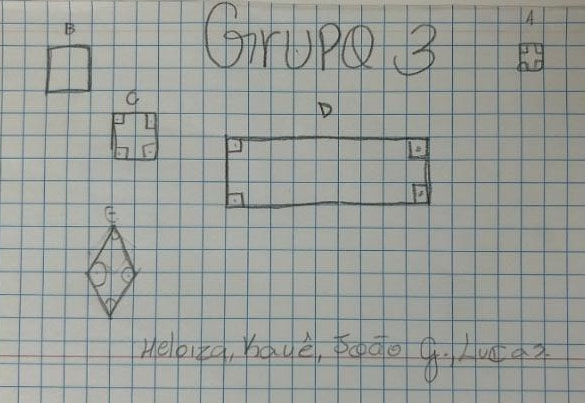
Figura 5: Produção do Grupo 3
O grupo conseguiu desenhar todos os quadriláteros e iniciou sua discussão sobre as propriedades do quadrado, considerando sua aplicabilidade em várias classificações. Essa reflexão sobre os atributos comuns entre as figuras foi uma oportunidade valiosa para consolidar o conhecimento.
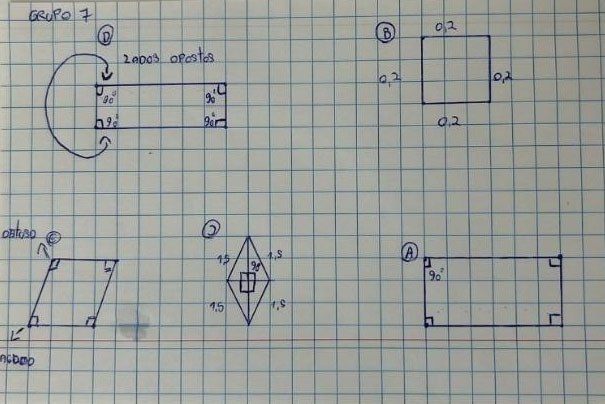
Figura 6: Produção do Grupo 7
Este grupo apresentou organização e completou a atividade dentro do tempo estipulado, inclusive passando caneta sobre os desenhos para maior clareza. Os alunos identificaram corretamente as relações entre os lados opostos e angulares, evidenciando uma compreensão aprofundada.
Essa experiência destaca a importância da ludicidade, como observa Rezende (2022), que assinala o crescente desenvolvimento de pesquisas nessa área, especialmente no segundo segmento do Ensino Fundamental. Ao incorporar o aspecto lúdico, atividades como essa incentivam os alunos a explorar a Matemática de maneira interativa e envolvente, promovendo um aprendizado mais profundo e significativo.
Considerações finais
Este relato de experiência atingiu seu objetivo principal ao explorar e implementar práticas pedagógicas colaborativas que promovem a equidade e a resolução de problemas no ensino de quadriláteros. Com as atividades realizadas, conseguimos responder à pergunta central da pesquisa, considerando a investigação das diversas habilidades e contextos sociais que os alunos apresentam.
As atividades colaborativas e a abordagem voltada para a resolução de problemas apresentados são estratégias para envolver os alunos, criando um ambiente propício para discussão rica sobre as propriedades geométricas. A análise de erros comuns, como a confusão entre paralelismo e congruência, foi importante para aprimorar futuras intervenções pedagógicas. Essa experiência destacou a importância de metodologias que garantam equidade, permitindo que todos os alunos, independentemente de suas habilidades, participem ativamente do processo de aprendizagem; além disso, observamos um desenvolvimento significativo em habilidades como comunicação, cooperação e pensamento crítico entre os grupos. Ao refletir sobre o tempo dedicado à revisão teórica e à divisão de tarefas, planejamos aprimorar as atividades futuras, garantindo mais espaço para investigação e produções coletivas.
Em resumo: a experiência reafirma a importância de integrar práticas pedagógicas que favoreçam a construção de conhecimentos aplicáveis em Matemática, pois, ao priorizar a exploração, a colaboração e o pensamento crítico, conseguimos oferecer aos alunos uma compreensão mais profunda das relações espaciais e estruturais nas figuras geométricas. Assim, esperamos não apenas enriquecer o conhecimento matemático dos estudantes, mas também prepará-los para enfrentar desafios futuros com confiança e habilidades essenciais.
Referências
BOALER, J. Mentalidades matemáticas: estimulando o potencial dos estudantes por meio da matemática criativa, das mensagens inspiradoras e do ensino inovador. Trad. Daniel Bueno; rev. técnica: Fernando Amaral Carnaúba, Isabele Veronese e Patricia Cândido. Porto Alegre: Penso, 2018.
BRASIL. MEC. Base Nacional Comum Curricular. Brasília: MEC/SEB, 2017.
COHEN, Elisabeth G.; LOTAN, Rachel. A. Planejando o trabalho em grupo: estratégias para salas de aula heterogêneas. Trad. Luís Fernando Marques Dorvillé, Mila Molina Carneiro e Paula Márcia Schumaltz Ferreira Rozin; rev. técnica: Mila Molina Carneiro e José Ruy Lozano. 3ª ed. Porto Alegre: Penso, 2017.
INSTITUTO CANOA. O Programa de Especialização Docente (PED Brasil). s/d. Disponível em: https://institutocanoa.org/ped-brasil/. Acesso em: maio 2024.
REZENDE, Christiano Henrique. Estudo do lúdico no ensino de Matemática: uma pesquisa bibliográfica exploratória. Revista Educação Pública, Rio de Janeiro, v. 22, nº 46, 13 de dezembro de 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/46/estudo-do-ludico-no-ensino-de-matematica-uma-pesquisa-bibliografica-exploratoria Acesso em: 13 out. 2024.
SÃO PAULO (Estado). Secretaria da Educação. Centro de Mídias de São Paulo. s/d. Disponível em: https://centrodemidiasp.educacao.sp.gov.br Acesso em: 13 out. 2024.
VAN DE WALLE, John. Matemática no Ensino Fundamental: formação de professores e aplicações em sala de aula. Trad. Paulo Henrique Colonese. 6ª ed. Porto Alegre: Artmed, 2009.
WIGGINS, G. J.; MCTIGHE, J. Planejamento para a compreensão: alinhando currículo, avaliação e ensino por meio da prática do planejamento reverso. 2ª ed. Porto Alegre: Penso, 2019.
Publicado em 03 de dezembro de 2025
Como citar este artigo (ABNT)
ALJBAAE, Samyra Faria Fontes; RICHETTO, Kátia Celina da Silva; FERREIRA, Willian José. Quadriláteros em ação: uma aventura colaborativa nos anos finais do Ensino Fundamental. Revista Educação Pública, Rio de Janeiro, v. 25, nº 46, 3 de dezembro de 2025. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/25/46/quadrilateros-em-acao-uma-aventura-colaborativa-nos-anos-finais-do-ensino-fundamental
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

