O jogo Trilha dos Restos: uma metodologia para o ensino de Matemática utilizando material concreto
Cristiane de Mello
UNIRIO
Daniela Mendes Vieira da Silva
Coordenadora do Projeto Laboratório Sustentável de Matemática (Seeduc/RJ), professora universitária (UCB e Cecierj), consultora do Sesi Nacional
Loisi Carla Monteiro Pereira
UNIRIO
Luzia da Costa Tonon Martarelli
UNIRIO
Mara Neves Lima Freire
UNIRIO
Marcelo Leonardo dos Santos Rainha
UNIRIO
O ensino teórico através de aulas expositivas ou a prática de exercícios repetitivos são ações apontadas por D’Ambrosio (2011, p. 119) como modelos ultrapassados que têm contribuído para o baixo rendimento no aprendizado da matemática e desmotivação dos alunos em sala de aula. Buscar experiências novas, que sejam capazes de modificar essa realidade, tem sido o desafio constante do professor na sua prática docente.
É notório que não existe um único ou melhor caminho para o ensino da Matemática, porém, conhecer metodologias que podem ser adotadas em sala de aula com a finalidade de obter um melhor aproveitamento do conteúdo por parte do aluno é de fundamental importância para que o professor construa sua prática em sala de aula. Contudo, esta ferramenta quando utilizada, não pode ser apresentada em caráter de passatempo, é necessário um planejamento adequado para obtenção dos resultados pretendidos.
Sendo assim, visando contribuir para a mudança deste cenário, elaboramos um questionário com o objetivo de fazer uma interação entre o lúdico e o conteúdo matemático trabalhado no jogo Trilha dos Restos, o qual será apresentado em detalhes na seção 3 deste artigo. Este questionário, elaborado para aplicação dessa metodologia, é de fundamental importância para que o aluno consiga perceber e compreender alguns conceitos matemáticos, como por exemplo: critérios de divisibilidade.
Este trabalho se justifica pela escassez de literatura acerca da importância e do papel do uso de questionários após a aplicação de jogos para a aprendizagem de Matemática e uma vez que a equipe Jogos & Matemática tem ampla experiência nesse tipo de metodologia.
O objetivo geral deste artigo é o de discutir a importância da elaboração e aplicação de um questionário voltado ao aprendizado decorrente da vivência de um jogo para aprender Matemática. Como objetivos específicos pretende-se aqui fazer uma discussão: do papel dos jogos na aprendizagem de Matemática, do jogo trilha dos restos e da construção de um questionário a partir da aplicação deste jogo visando generalizar a importância do questionário para os demais jogos tendo em vista a aprendizagem matemática.
Ao longo deste artigo, apresentamos: algumas definições de jogo, encontradas na literatura; as vantagens de usar jogos em um programa matemático; o jogo Trilha dos Restos; justificaremos a escolha dos números dispostos no tabuleiro deste jogo - apontando, em particular, a relevância didática dos números 0 e 60 – e listamos algumas metas que podem ser alcançadas com a aplicação dele; exibimos os problemas que constituem o questionário relacionado à proposta lúdica que utiliza o jogo Trilha dos Restos, fundamentamos a escolha deles e fazemos um relato sucinto dos objetivos que cercam cada um deles, discutindo a importância do uso de um questionário especialmente elaborado para consolidar o aprendizado ocorrido durante a aplicação do jogo supracitado, assim como generalizamos esta ideia para a aplicação de jogos para aprender Matemática.
O que é jogo e as vantagens de usar jogos no processo de ensino-aprendizagem
Sabemos que na literatura encontramos muitas definições de jogo. Apresentamos duas delas:
- “Um jogo é uma representação formal de uma situação em que vários indivíduos interagem em um ambiente de interação estratégica. Com isso, queremos dizer que a dinâmica de bem-estar dos indivíduos envolvidos depende não apenas de suas próprias ações, mas também das ações de outros indivíduos” (Mas-Colell, 1995, p. 219, tradução nossa);
- “O jogo é um tipo de atividade que alia raciocínio, estratégia e reflexão com desafio e competição de uma forma lúdica muito rica. Os jogos de equipe podem ainda favorecer o trabalho cooperativo” (Currículo Nacional do Ensino Básico, s/d, p. 68).
Essas são apenas algumas definições de jogo; existem muitas outras matematicamente mais rigorosas que envolvem problemas como o famoso Dilema do Prisioneiro (Poundstone, 1993), que tentam modelar situações sociais de tomadas de decisão, que não é o objetivo deste trabalho. No livro Homo Ludens: o jogo como elemento da cultura, Huizinga reflete sobre o jogo como elemento da cultura e não apenas como elemento na cultura (Huizinga, 2004). Trata-se de entender o jogo em si, enquanto fenômeno cultural e sua importância fundamental para o desenvolvimento das culturas e civilizações, tendo o elemento jogo como forma significante da função social.
Tais preceitos vão ao encontro a amalgamar o interacionismo de Vygotsky (1995), em que o homem sofre influência da cultura e da história na qual está mergulhado. O jogo então, como objeto, está inserido em qualquer comunidade e devemos encará-lo como prática social que tem como último fim promover o desenvolvimento humano cognitivo. Cabe ainda ao mediador, que traz o jogo a ser desenvolvido em sua pequena sociedade, ter a sensibilidade de adaptá-lo, aproximando a experiência histórico-cultural dos participantes. Isso também corrobora ao interacionismo de Paulo Freire (1999, 2005), em que o homem deve ser compreendido como uma totalidade e não como um sujeito isolado. Durante a prática do jogo, ainda é possível fazer uma série de avaliações subjetivas; é possível analisar a forma de agir e pensar criticamente em um ambiente controlado, analisar a aptidão ao risco e o amadurecimento das capacidades lógica e emocional.
Independentemente do que sejam precisamente os jogos ou da forma como cada sociedade se organiza para jogar, o jogo está presente. Mesmo nas salas de aula ditatoriais, existem jogos não declarados sendo jogados.
Para Barros (2019),
os jogos didáticos têm grande importância no desenvolvimento cognitivo dos alunos, pois atuam no processo de apropriação do conhecimento, permitindo o desenvolvimento de competências, o desenvolvimento espontâneo e criativo, além de estimular capacidades de comunicação e expressão, no âmbito das relações interpessoais, da liderança e do trabalho em equipe. De maneira lúdica, prazerosa e participativa o estudante irá relacionar-se com o conteúdo escolar, levando esse aluno a uma maior apropriação dos conhecimentos envolvidos.
Diante do quadro escolar em que o nosso país se encontra, o projeto Jogos & Matemática oferece aos indivíduos, através de jogos tanto digitais quanto de material concreto, uma acentuada interação olho no olho, o que reforça o ato de troca, contribuindo assim para o processo de ensino-aprendizagem. Com alto grau de criatividade e baixo custo de confecção, os jogos acabam por promover a tão desejada motivação nas salas de aula.
Os Parâmetros Curriculares Nacionais de Matemática (Brasil, 1998, p. 46), do Ministério da Educação (MEC), em relação à inserção de jogos no ensino de Matemática, pontuam que eles constituem uma forma interessante de propor problemas, pois permitem que:
sejam apresentados de modo atrativo e favorecem a criatividade na elaboração de estratégias de resolução de problemas e busca de soluções. Propiciam a simulação de situações-problema que exigem soluções vivas e imediatas, o que estimula o planejamento das ações.
Segundo Wiersum (2012, p. 24), “as vantagens de usar jogos em aulas de Matemática foram resumidas em um artigo de Davies (1995)”. Listamos a seguir alguns dos pontos mais relevantes para a equipe.
- Situações significativas para a aplicação de habilidades matemáticas.
- Os jogos oferecem oportunidades para construir autoconhecimento e desenvolver atitudes positivas em relação à Matemática, reduzindo o medo de falhas e erros.
- Em comparação com atividades mais formais, uma melhor aprendizagem pode ocorrer através de jogos devido à maior interação entre crianças e ao maior número de oportunidades para testar ideias intuitivas e estratégias de resolução de problemas.
- Os jogos podem permitir que as crianças operem em diferentes níveis de pensamento e aprendam umas com as outras. Em um grupo de crianças que jogam um determinado jogo, uma criança pode estar encontrando um conceito pela primeira vez, outra pode estar desenvolvendo sua compreensão do conceito, uma terceira consolidando conceitos previamente aprendidos.
- O pensamento das crianças muitas vezes se torna aparente através das ações e decisões que elas fazem durante um jogo, então o professor tem a oportunidade de realizar o diagnóstico e a avaliação do aprendizado em uma situação não ameaçadora.
- As crianças podem trabalhar independentemente do professor. As regras do jogo e a motivação das crianças geralmente as mantêm em tarefa.
- Um benefício adicional torna-se evidente quando crianças de culturas diferentes estão envolvidas. As estruturas básicas de alguns jogos são comuns a muitas culturas e os procedimentos de jogos simples podem ser rapidamente aprendidos através da observação. Crianças que são relutantes em participar de outras atividades matemáticas, por causa das barreiras culturais, frequentemente se juntam em um jogo, e assim ganham acesso à aprendizagem matemática, além de se engajarem em uma interação social estruturada (tradução nossa).
O trabalho com jogos educacionais desenvolve habilidades como avaliação e senso moral de si e do grupo ao qual a criança está inserida, incentivando a cooperação e competições sadias entre os pares. Além do teor teórico envolvido em cada jogo, são trabalhadas, em diversas camadas de entendimento, a interpretação e as dificuldades através de um questionário para o aluno, elaborado cuidadosamente pela equipe para induzir o mesmo a alcançar o objetivo proposto em cada atividade. Na sequência, apresentaremos a descrição do jogo Trilha dos Restos e a metodologia utilizada.
O jogo Trilha dos Restos
Trata-se de um jogo que pode ser facilmente acessado na internet. Para este trabalho, consideramos o formato de tabuleiro proposto no site da Diretoria de Ensino Fundamental - Matemática da Prefeitura Municipal de São Vicente/SP. Também conhecido como Trilha do Resto, Avançando com o resto, Caminhando com o resto, Jogo do resto, o jogo Trilha dos Restos é destinado a alunos que já tenham sido apresentados aos conceitos de multiplicação e divisão.
Como as ideias de divisão entre números naturais começam a aparecer no segundo ano do Ensino Fundamental I, ainda que de maneira não formalizada, seguindo recomendações dos Parâmetros Curriculares Nacionais (Brasil, 1998), e se prolongam nos demais anos, esse jogo é um jogo indicado para os alunos deste ciclo, mas, devido à realidade que enfrentamos atualmente no ensino de Matemática, dos 79 países avaliados, o Brasil ficou em 70ª posição em Matemática no PISA 2018 (Todos pela Educação, 2018). Só pra lembrar, o Pisa – Programa Internacional de Avaliação de Alunos – é uma avaliação internacional que mede o nível educacional de jovens de 15 anos por meio de provas de Leitura, Matemática e Ciências.
Conforme mencionado, embora as ideias de divisão entre números naturais comecem a aparecer no segundo ano do Ensino Fundamental I, dependendo do objetivo que se deseja alcançar, este jogo pode ser aplicado em diferentes anos do Ensino Básico e até mesmo no Ensino Superior, com outra perspectiva de ensino. O que diferencia o público-alvo a ser atingido é a abordagem do questionário do aluno.
O material necessário para a confecção do jogo consiste em um tabuleiro feito em um pedaço de papel-cartão (ou cartolina), um dado de seis faces e dois marcadores que representarão a movimentação dos jogadores, os chamados peões. Tais marcadores podem ser feitos de papel, EVA ou de material reciclável, como tampas de garrafas plásticas.
O jogo Trilha dos Restos foi confeccionado pela equipe Jogos & Matemática, da Universidade Federal do Estado do Rio de Janeiro (UNIRIO), que é composta por professores do Departamento de Matemática (DMAT) da universidade, professores colaboradores, da UNIRIO e de outras universidades, e por alunos do curso de Licenciatura em Matemática da UNIRIO, sendo alguns bolsistas e outros voluntários; a equipe era formada inicialmente pelos professores Cristiane de Mello, Loisi Carla, Luzia Tonon e Marcelo Rainha, com os respectivos projetos de Extensão: Divulgando os jogos matemáticos nas mídias digitais; Curiosidades e passatempos: o outro lado da Matemática; Jogos para o ensino de contagem e A Geometria contra-ataca, que tinham um objetivo comum: apresentar novas metodologias de aprendizagem no ensino de Matemática, não só para licenciandos de Matemática como também para professores que lecionam no Ensino Básico das redes públicas e privadas do Estado do Rio de Janeiro.
Na Figura 1 apresentamos o jogo Trilha dos Restos.
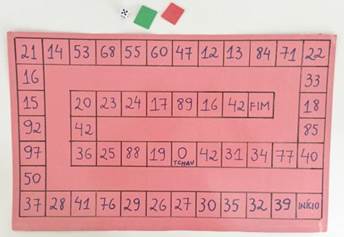
Figura 1: Tabuleiro do jogo Trilha dos Restos
O jogo Trilha dos Restos pode ser disputado entre equipes ou individualmente. Para iniciar o jogo, os peões posicionam-se na casa Início. O professor pede que cada equipe lance o dado e mova seu peão no tabuleiro de acordo com o número sorteado no dado. Em seguida, o professor explica que as próximas movimentações dos peões corresponderão aos restos obtidos nas divisões que serão efetuadas no jogo e apresenta as regras.
Regras
De acordo com Borim (2004), as regras do jogo Trilha dos Restos são:
- Duas equipes jogam alternadamente.
- Na primeira rodada, cada equipe posiciona seu peão na casa Início, lança o dado e movimenta seu peão de acordo com o número sorteado no dado.
- A partir da segunda rodada, cada equipe lança o dado e faz uma divisão em que:
- o dividendo é o número da casa onde seu peão está;
- o divisor é o número sorteado no dado.
- Em seguida, cada equipe calcula o resultado da sua divisão e movimenta seu peão o número de casas igual ao resto dessa divisão.
- A equipe que efetuar um cálculo errado perde a sua vez de jogar.
- Cada equipe deverá obter um resto que faça seu peão chegar exatamente à casa Fim sem ultrapassá-la, mas se isso não for possível, ela perde a vez de jogar e seu peão fica no mesmo lugar.
- Vence a equipe que chegar primeiro com seu peão à casa Fim.
Por que jogar Trilha dos Restos?
O jogo Trilha dos Restos é rico em conhecimentos matemáticos e pode ser bastante explorado. Além de desenvolver no aluno atitudes de interação, colaboração e troca de experiências em grupo, o jogo estimula o aluno a aprender o conteúdo matemático abordado nele para tentar atingir a tão desejada vitória. A relação entre o divisor e o número de possibilidades para o resto em uma determinada divisão é avaliada e discutida neste jogo. Como o peão anda de acordo com o resto das divisões e vence a equipe que chegar primeiro na casa Fim, é de interesse comum obter o maior resto possível nas divisões. Nesse sentido, confrontamos a tradição de que uma divisão para ser boa tem que ser exata, ou seja, dar resto zero, do ponto de vista do jogo isso não se aplica, uma divisão exata não é esperada porque não ajuda a alcançar a vitória. Ultrapassamos, assim, a primeira barreira: o aluno desenvolve seus cálculos sem temer um resultado não exato; na verdade, ele está à procura dele.
Dentre os muitos objetivos que podem ser alcançados com a aplicação do jogo Trilha dos Restos estão:
- Aumentar a concentração e desenvolver habilidades de raciocínio;
- Exercitar cálculos mentais que envolvem multiplicação e divisão;
- Entender a importância do resto em uma divisão;
- Identificar o número 1 como divisor de qualquer número (quando o número 1 é sorteado no dado, o peão não anda, independente da casa onde ele esteja);
- Observar que todo número par é divisível por 2 (quando o número 2 é sorteado no dado, o peão não anda se estiver em uma casa com um número par);
- Descobrir que todo número possui uma quantidade finita de divisores (quando o aluno perceber a desvantagem de ter seu peão em uma casa com muitos divisores, por exemplo, na casa 12: a possibilidade de sortear no dado o único número que não divide 12, ou seja, o número 5, é baixa e provavelmente seu peão ficará parado por algumas rodadas);
- Reforçar a definição de número primo (quando o aluno perceber a vantagem de ter seu peão em uma casa com um número primo, pois, neste caso, como só temos os primos 2, 3 e 5 no dado e todas as casas são maiores do que 11, o peão avançará independente do número sorteado no dado, diferente de 1);
- Reconhecer e aplicar os critérios de divisibilidade por 2, 3, 4, 5 e 6;
- Entender que o resto de uma divisão é sempre menor que o divisor, observando que o número sorteado no dado é sempre maior que a movimentação do peão.
A importância da Casa 60 e da Casa 0 Tchau
O tabuleiro do jogo Trilha dos Restos pode ser confeccionado utilizando diversos números aleatórios. A escolha desses números pode ser alterada dependendo do ano escolar em que o jogo será aplicado. O professor pode escolher números maiores ou menores, primos ou não, levando em consideração o nível da sua turma. Para os números que colocamos no tabuleiro da última figura, dois, em especial, merecem a nossa atenção: 0 e 60. Na verdade, existe uma razão especial para ambos pertencerem à nossa escolha, e é disso que trataremos neste tópico.
- Casa 60: Quando algum peão cai na Casa 60 pela primeira vez no jogo, os alunos costumam seguir o jogo normalmente sem darem muita importância a esse fato. Lançam o dado uma, duas, três, até mais vezes e só então começam a perceber que seu peão não se move! A partir deste momento, começam a surgir os questionamentos: “Será que o peão não vai sair dessa casa?”, “Qual número deve ser sorteado no dado para que o peão se mova?” etc. O professor é então chamado e deve provocar ainda mais essa discussão. Não dar a resposta imediatamente é essencial porque o intuito é exatamente este: incentivar os alunos a pensarem e a tirarem suas próprias conclusões. Depois de devidamente analisados os questionamentos, os alunos finalmente desvendam o mistério da casa 60: todos os números do dado são divisores de 60 e, independente do número sorteado no dado, o peão não irá se mover! Aí logo vem a pergunta da equipe representada pelo peão: “Então, perdemos?”. Neste instante, o professor pode, e deve, revelar a ‘regra oculta’ do jogo: “Não. Seu peão andará 6 casas!”. Agora, satisfeitos e aliviados, todos voltam a jogar normalmente. A missão da Casa 60 foi cumprida com louvor.
- Casa 0 Tchau: Se tem uma casa que chama a atenção antes mesmo de qualquer explicação desse jogo, essa é, sem dúvida, a Casa 0 Tchau. Ela nem é citada nas regras, mas pelo “Tchau” em seu nome, todos automaticamente entendem a mensagem: ‘Se cair na Casa 0 Tchau, está fora do jogo! Perdeu!’. A partir daí, todos lançam o dado torcendo muito para que seu peão não caia na Casa 0 Tchau. À medida que o peão se aproxima da Casa 0 Tchau, a tensão aumenta e só passa quando o peão escapa da Casa 0 Tchau. Ao término do jogo, o alívio é geral porque nenhum peão da turma caiu na tão temida casa! Alguns até arriscam um palpite: “É sorte!”, mas a verdade é que isso é pura Matemática! Nenhum peão cairá na Casa 0 Tchau (esta é a razão pela qual a mesma não é citada nas regras!) e o professor deve aproveitar esse interesse dos alunos para explicar o porquê. Como o maior número que pode ser sorteado no dado é 6, o maior resto possível nesse jogo é 5. Assim, temos que avaliar os possíveis restos das casas de número 40, 77, 34, 31 e 42:
- Os restos das divisões de 40 por 1, 2, 3, 4, 5 e 6 são, respectivamente: 0, 0, 1, 0, 0 e 4;
- Os restos das divisões de 77 por 1, 2, 3, 4, 5 e 6 são, respectivamente: 0, 1, 2, 1, 2 e 5;
- Os restos das divisões de 34 por 1, 2, 3, 4, 5 e 6 são, respectivamente: 0, 0, 1, 2, 4 e 4;
- Os restos das divisões de 31 por 1, 2, 3, 4, 5 e 6 são, respectivamente: 0, 1, 1, 3, 1 e 1;
- Os restos das divisões de 42 por 1, 2, 3, 4, 5 e 6 são, respectivamente: 0, 0, 0, 2, 2 e 0.
Em qualquer um dos casos avaliados, o peão não cai na Casa 0 Tchau. Desse modo, o professor aproveita a oportunidade causada pela curiosidade dos alunos para apresentar e debater conceitos que envolvem divisibilidade e resto. Este era o principal objetivo da Casa 0 Tchau, e o mesmo foi atingido com sucesso.
Cabe ressaltar que os números alocados nas cinco casas antes da Casa 0 Tchau são de suma importância para que o peão não caia na mesma. Sendo assim, o professor que fizer alterações nos números dispostos no tabuleiro deve estar atento a este fato.
Questionário do aluno
Entende-se ser importante que se traga à discussão questionários elaborados a partir da junção entre teoria, prática e Matemática, e que esse recurso metodológico seja aplicado a fim de deixar claro para os alunos os conceitos matemáticos abordados no jogo e até mesmo auxiliar na construção do conhecimento matemático por parte do aluno.
A Base Nacional Comum Curricular (Brasil, 2017)
orienta-se pelo pressuposto de que a aprendizagem em Matemática está intrinsecamente relacionada à compreensão, ou seja, à apreensão de significados dos objetos matemáticos, sem deixar de lado suas aplicações. Os significados desses objetos resultam das conexões que os alunos estabelecem entre eles e os demais componentes, entre eles e seu cotidiano e entre os diferentes temas matemáticos. Desse modo, recursos didáticos como malhas quadriculadas, ábacos, jogos, livros, vídeos, calculadoras, planilhas eletrônicas e softwares de Geometria dinâmica tem um papel essencial para a compreensão e utilização das noções matemáticas. Entretanto, esses materiais precisam estar integrados a situações que levem à reflexão e à sistematização, para que se inicie um processo de formalização.
Diante do exposto, constatamos que faz-se necessário refletir sobre o que se busca com o jogo, pois, “quando bem elaborados, eles podem ser vistos como uma estratégia de ensino que poderá atingir diferentes objetivos que variam desde o simples treinamento até a construção de determinado conhecimento” (Lara, 2007, p. 21).
No entanto, percebemos que, inicialmente, o jogo era aplicado sem o questionário do aluno, pois o mesmo não existia; aplicava-se apenas o jogo do tabuleiro. Porém, após inúmeras aplicações, com licenciandos em Matemática de diferentes lugares, identificamos que os mesmos não estavam atentos ao que ocorria na casa de número 60, conforme explicado no item anterior; ficavam parados por, pelo menos, quatro rodadas sem conseguir perceber que 60 é um número múltiplo de todos os números do dado e, consequentemente, era impossível sair de tal casa.
Nesse momento, foi constatada a necessidade de criar um questionário do aluno com essa finalidade, ou seja, fazer com que o aluno compreenda os conceitos inseridos no jogo. Após essa análise, também confirmamos a necessidade de inserir uma discussão referente à Casa 0 Tchau, pois, até então, os alunos acreditavam ser possível cair na mesma.
Ao inserir no questionário uma questão com o objetivo de discutir o que ocorre na casa de número 60, os alunos passaram a ficar mais atentos e, consequentemente, conseguiam responder também à questão referente à Casa 0 Tchau. Isso confirma a extrema importância da elaboração do questionário do aluno.
O questionário do aluno é apresentado na Figura 1.

Figura 1: Questionário do aluno
A seguir, apresentaremos os objetivos específicos de cada questão proposta no questionário do aluno.
- O objetivo desta questão é reforçar que o número sorteado no dado (neste caso, o 5) é sempre maior que a movimentação do peão. Além de enfatizar que quanto mais próximo de um múltiplo de 5, menos casas o peão andará.
- O objetivo dessa questão é fazer com que o aluno observe que todos os números do dado são divisores de 60, pois o mesmo é o único número presente em todas as listas acima (todos os números do dado são divisores de 60).
- Após a análise feita na questão anterior, o aluno consegue responder a este item. Além disso, conseguimos chamar a atenção para este fato do aluno cujo peão não tenha caído na casa de número 60 durante o jogo e este número tenha passado despercebido.
- Após a realização das questões anteriores, o aluno neste ponto já consegue identificar a impossibilidade de o peão cair na Casa 0 Tchau, conforme explicado.
Considerações finais
Ao longo do artigo, discutimos a importância da inserção de uma metodologia que utiliza material concreto para auxiliar a aprendizagem matemática. Após aplicarmos algumas vezes o jogo de tabuleiro Trilha dos Restos, com licenciandos em Matemática de diferentes lugares, constatamos a necessidade da confecção de um novo recurso que deixasse mais claro para o aluno, o que ocorria com algumas casas importantes no jogo.
O questionário do aluno foi confeccionado com o objetivo de inserir uma discussão sobre o que ocorre com a Casa 60 e a Casa 0 Tchau no jogo. Esse questionário é aplicado logo após os alunos terem contato com o jogo. E a partir dele, os alunos começaram a ficar mais atentos ao que acontecia com as referidas casas durante o jogo - o que confirmou a extrema importância da elaboração do questionário do aluno.
O trabalho com jogos educacionais desenvolve habilidades como avaliação e senso moral de si e do grupo ao qual a criança está inserida, incentivando a cooperação e competições sadias entre os pares. Além do teor teórico envolvido em cada jogo, são trabalhadas, em diversas camadas de entendimento, a interpretação e as dificuldades através de um questionário para o aluno, elaborado cuidadosamente pela equipe para induzir o mesmo a alcançar o objetivo proposto em cada atividade.
Nosso objetivo com este trabalho, mais do que mostrar a importância da utilização de jogos de material concreto no ensino de Matemática, é revelar os efeitos positivos e imediatos da aplicação de um questionário, que contenha problemas relacionados aos conteúdos matemáticos velados no jogo, como complemento da proposta lúdica que envolve o jogo, para a aprendizagem do aluno.
A experiência desta equipe percebe que o ensino de Matemática está em mutação: a nova sala de aula coloca o professor como um mediador da aprendizagem, isto é, o professor passa a ser o fomentador de perguntas para as quais cada aluno deve procurar suas próprias respostas. Essa nova sala de aula propõe uma aula que, apesar de coletiva, viabiliza o entendimento e a aprendizagem singular de cada indivíduo. Neste contexto, o jogo Trilha dos Restos surge como uma ferramenta exemplar. Apesar de não ter sido criado pela equipe, experimentamos sua aplicação em diversos níveis: para professores da rede que ensinam Matemática, alunos de licenciatura em Matemática e Pedagogia, alunos do ensino médio e fundamental. O jogo Trilha dos Restos sempre teve uma ótima receptividade. Acreditamos que uma das razões para tal sejam suas muitas camadas, que permitem sua aplicação com as mesmas regras para todos os públicos.
Contudo, como o jogo pelo jogo não é o foco desta equipe – ao contrário, desejamos lograr ao máximo suas potencialidades como ferramenta de ensino –, elaboramos um questionário “personalizado” para o aluno. Diferente da aplicação do jogo em si, a resolução deste questionário depende do nível de conhecimento matemático que o aluno possui e, portanto, cabe ao professor diagnosticar a viabilidade de aplicá-lo ou não para os seus alunos. Independente do jogo considerado, é irrefutável a importância de um questionário como complemento da atividade que o envolve porque é através do questionário que se revelam as habilidades matemáticas “escondidas” nas regras e na dinâmica do jogo.
No caso específico do jogo Trilha dos Restos, o questionário induz o aluno a desvendar os mistérios dos números dispostos no tabuleiro. A professora Loisi Carla explica isso didaticamente em detalhes nos vídeos Jogo Trilha dos Restos – Parte 1 e Jogo Trilha dos Restos – Parte 2, disponíveis no canal Jogos & Matemática UNIRIO no YouTube.
Como trabalhos futuros, faremos a análise das respostas dos questionários aplicados para alunos da rede pública e particular do estado do Rio de Janeiro. Este trabalho também visa contribuir para a área de metodologia de aplicação de jogos juntamente com questionários para a verificação da aprendizagem matemática por parte do aluno, que convive com uma escassez de pesquisa no momento.
Referências
BARROS, M. G. F. B.; MIRANDA, J. C.; COSTA, R. C. Uso de jogos didáticos no processo ensino-aprendizagem. Educação Pública, v. 19, n. 23, out. 2019. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/19/23/uso-de-jogos-didaticos-no-processo-ensino-aprendizagem. Acesso em: 10 jun. 2020.
BORIM, J. Jogos e resoluções de problemas: uma estratégia para as aulas de Matemática. 5ª edição. São Paulo: CAEM/IME-USP, 2004.
BRASIL. Base Nacional Comum Curricular. Brasília: MEC/Consed/Undime, 2017.
BRASIL. Parâmetros Curriculares Nacionais – Introdução. Ensino Fundamental. Brasília: MEC/SEF, 1998.
CURRÍCULO NACIONAL DO ENSINO BÁSICO. Disponível em: https://alvarovelho.net/attachments/article/39/LivroCompetenciasEssenciais.pdf.Acesso em: 15 jun. 2020.
DAVIES, B. The role of games in mathematics. Square One, v. 5, nº 2, 1995.
D’AMBROSIO, Ubiratan. Educação Matemática: da teoria à prática. 22ª ed. Campinas: Papirus, 2011.
DIRETORIA DE ENSINO FUNDAMENTAL. Matemática. Disponível em: http://fundamentalmatsv.blogspot.com/2010/05/trilha-da-divisao.html. Acesso em: 7 jul. 2020.
FERREIRA, R. J. da S. O uso do jogo do varal dos números racionais como metodologia de ensino de Matemática em sala de aula. Educação Pública, v. 20, nº 1, jan. 2020. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/20/1/o-uso-do-jogo-do-varal-dos-numeros-racionais-como-metodologia-de-ensino-de-matematica-em-sala-de-aula. Acesso em: 10 jul. 2020.
FREIRE, Paulo. Educação como prática da liberdade. 23ª ed. Rio de Janeiro: Paz e Terra, 1999.
FREIRE, Paulo. Pedagogia do Oprimido. 41ª ed. Rio de Janeiro: Paz e Terra, 2005.
HUIZINGA, J. Homo Ludens: o jogo como elemento da cultura. 4ª ed. Trad. João Paulo Monteiro. São Paulo: Perspectiva, 2007.
JOGOS. Jogos & Matemática. Rio de Janeiro, s/d. Disponível em: https://jogosmatunirio.wordpress.com/jogos. Acesso em: 10 jun. 2019.
LARA, I. C. M. Exames nacionais e as ‘verdades’ sobre a produção do professor de Matemática. 248 f. Tese (Doutorado), Programa de Pós-Graduação em Educação, Faculdade de Educação, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2007.
MAS-COLELL, A.; WHINSTON, M.; GREEN, J. Microeconomic theory. New York: Oxford University Press, 1995.
PETRONI, A. P.; SOUZA, V. L. T. de. Vygotsky e Paulo Freire: contribuições para a autonomia do professor. Rev. Diálogo Educ., Curitiba, v. 9, nº 27, p. 351-361, 2009.
POUNDSTONE, W. Prisoner`s Dilemma. New York: Anchor Books, 1993.
TODOS PELA EDUCAÇÃO. Pisa 2018: para voltar a avançar, Brasil precisa investir na profissionalização e no prestígio da carreira dos professores. Disponível em: https://www.todospelaeducacao.org.br/conteudo/Pisa-2018. Acesso em: 03 ago. 2020.
VÍDEOS. Jogos & Matemática UNIRIO. Disponível em: https://www.youtube.com/channel/UCxIt7eDsp6w2q-DrYDkSk6Q. Acesso em: 10 jul. 2020.
VYGOTSKY, L. S. Obras escogidas III: problemas del desarrollo de la psique. Madrid: Visor, 1995.
WIERSUM, E. G. Teaching and learning Mathematics through games and activities. Acta Electrotechnica et Informatica, v. 12, nº 3, p. 23-26, 2012. doi: 10.2478/v10198-012-0026-2.
Publicado em 02 de fevereiro de 2021
Como citar este artigo (ABNT)
MELLO, Cristiane de; SILVA, Daniela Mendes Vieira da; PEREIRA, Loisi Carla Monteiro; MARTARELLI, Luzia da Costa Tonon; FREIRE, Mara Neves Lima; RAINHA, Marcelo Leonardo dos Santos. O jogo Trilha dos Restos: uma metodologia para o ensino de Matemática utilizando material concreto. Revista Educação Pública, v. 21, nº 4, 2 de fevereiro de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/4/o-jogo-itrilha-dos-restosi-uma-metodologia-para-o-ensino-de-matematica-utilizando-material-concreto
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

