Explorando funções afins a partir do jogo dos palitos
Rogério César dos Santos
Doutor em Educação
Wescley Well Vicente Bezerra
Doutor em Educação
Nas discussões educacionais atuais, tem-se refletido amplamente sobre formas de reorganizar o ensino da Matemática, buscando implementar práticas pedagógicas que tratem os conteúdos de maneira menos mecânica e mais significativa. Nesse contexto, o uso de jogos em sala de aula pode ser uma estratégia promissora para o desenvolvimento de habilidades matemáticas essenciais.
Um tema relevante para ser explorado por meio de jogos são as funções, especialmente as funções afins. Esse conteúdo é de grande importância na Educação Básica e possui aplicações em diversas áreas da ciência, principalmente em problemas relacionados à quantificação e variação de fenômenos naturais. Em outras palavras: trata-se de um tema que aborda grandezas que variam e podem ser representadas por um modelo matemático. No entanto, como apontado por Booth (1995), Radford (1996) e Ursini e Trigueros (2000), muitos estudantes enfrentam dificuldades na compreensão do conceito de variável e no trabalho com expressões algébricas e generalizações, o que torna necessário o uso de abordagens alternativas, como a aplicação de jogos, para o ensino desse conteúdo.
Diante disso, o jogo educativo ou pedagógico se apresenta como uma estratégia eficaz que motiva o ensino matemático das funções lineares, conciliando o aspecto lúdico aos objetivos pedagógicos. Azevedo (2015, p. 30) explica que
o século XX é marcado por uma discussão entre liberdade de expressão (que remete ao lúdico), promovida pelo jogo, versus atividade dirigida e orientada para objetivos e resultados estabelecidos. Buscando conciliar esses dois aspectos – o prazer e a aquisição de conteúdos –, temos um tipo de jogo específico, o jogo pedagógico ou educativo.
Com isso, considerando a necessidade de deixar o modelo tradicional de ensino da Matemática, este artigo tem como objetivo demonstrar uma alternativa para trabalhar o conteúdo de funções afins por meio da utilização do jogo dos palitos.
Jogos matemáticos em sala de aula
O uso de jogos nas aulas de Matemática pode romper com as abordagens tradicionais dessa disciplina, contribuindo para o desenvolvimento de diversas habilidades nos estudantes. Como apontam Smole, Diniz e Cândido (2007, p. 11),
em se tratando de aulas de Matemática, o uso de jogos implica uma mudança significativa nos processos de ensino e aprendizagem, que permite alterar o modelo tradicional de ensino, o qual muitas vezes tem no livro e em exercícios padronizados seu principal recurso didático. O trabalho com jogos nas aulas de matemática, quando bem planejado e orientado, auxilia o desenvolvimento de habilidades como observação, análise, levantamento de hipóteses, busca de suposições, reflexão, tomada de decisão, argumentação e organização, que estão estreitamente relacionadas ao chamado raciocínio lógico.
De acordo com os mesmos autores (Smole; Diniz; Cândido, 2007, p. 17-21), o uso de jogos em sala de aula exige dos professores um planejamento que contemple a apresentação do jogo aos alunos, a organização da classe para sua realização, o planejamento do tempo de jogo e a exploração dos conteúdos matemáticos envolvidos.
Além disso, Ciríaco (2022) destaca que os jogos nas aulas de Matemática oferecem uma oportunidade para os estudantes aprenderem de maneira descontraída, fortalecendo o vínculo entre professor e estudante. Essa abordagem também permite que os educadores identifiquem as eventuais dificuldades enfrentadas pelos alunos.
No entanto, é importante salientar que o jogo, por si só, não garante a aprendizagem matemática. Ele precisa ser inserido em um contexto escolar que promova a reflexão e a discussão, com o professor desempenhando o papel imprescindível de mediador. Sobre essa questão, Fiorentini e Miorim (1990) alertam que o professor não deve privilegiar um determinado material apenas por ser atraente ou lúdico, negligenciando sua metodologia de ensino.
Funções afins
Segundo Lima (2013, p.79), “uma função f:R→R chama-se afim quando existem constantes a, b ∈ R tais que f(x)=ax+b para todo x ∈ R". É importante ressaltar que as funções afins também são conhecidas como funções polinomiais do primeiro grau. Além disso, quando b=0, essas funções são conhecidas como funções lineares e estão associadas a problemas de proporcionalidade. O gráfico da função afim é uma linha reta; ‘a’ é conhecido como coeficiente angular da reta e ‘b’, o coeficiente linear, é a ordenada do ponto onde o gráfico da função f(x) intersecta o eixo OY (Lima, 2013, p. 81).
Devido à sua relevância, o tema das funções afins, ou funções polinomiais de primeiro grau, está presente na Base Nacional Comum Curricular (BNCC). Entre as habilidades relacionadas a esse conteúdo, destacam-se:
(EM13MAT302) Construir modelos empregando as funções polinomiais de 1º ou 2º graus, para resolver problemas em contextos diversos, com ou sem apoio de tecnologias digitais.
(EM13MAT401) Converter representações algébricas de funções polinomiais de 1º grau em representações geométricas no plano cartesiano, distinguindo os casos nos quais o comportamento é proporcional, recorrendo ou não a softwares ou aplicativos de álgebra e geometria dinâmica (Brasil, 2018, p. 543).
Dessa forma, o estudo das funções afins, por ser um tipo de função simples, pode favorecer a compreensão dos estudantes sobre o conceito de funções, domínio e imagem, especialmente sobre a relação de dependência entre duas variáveis e suas representações algébricas, numéricas e gráficas.
Descrição do jogo dos palitos
O jogo dos palitos é um recurso desenvolvido para uma única pessoa, proposto inicialmente por Vignatti e Brito (2014) e posteriormente generalizado por Cerqueira, Santos e Porto (2023). Neste artigo, será apresentada uma abordagem para utilizar o jogo como ferramenta para ensinar ou reforçar o conceito de função polinomial do primeiro grau a estudantes que estejam entrando em contato com funções pela primeira vez. Além disso, será explorado como trabalhar os conceitos de domínio e imagem de uma função por meio dessa atividade lúdica. Caso não haja palitos disponíveis, podem ser utilizadas cartas de baralho.
O jogo dos palitos é executado com uma quantidade q par de palitos: q=4n+4, sendo n qualquer número natural positivo. A execução do jogo se dá da seguinte maneira: fixado n natural positivo, dispõem-se os 4n+4 palitos sobre uma mesa, um ao lado do outro. O objetivo é movimentar um palito de cada vez para formar pares. Para isso, as seguintes regras devem ser observadas:
- Cada palito deve pular sobre t=2n palitos em cada movimento, para fazer par com o próximo palito;
- Uma vez formado o par, o mesmo não poderá mais ser mexido;
- Deve-se pular sobre t=2n palitos, seja sobre palitos individuais, seja sobre aqueles já formados em pares;
- O jogo termina quando todos os palitos estiverem em pares.
Uma estratégia vencedora apresentada por Cerqueira, Santos e Porto (2023), com n=1, começando com q=4n+4=4.1+4=8 palitos e saltos de tamanho t=2n=2.1=2, está ilustrada na Figura 1, em quatro passos. Os quatro palitos do centro pulam, um de cada vez, invertendo o sentido do salto em cada etapa. A numeração romana I, II, III e IV indica qual palito está pulando na respectiva etapa.
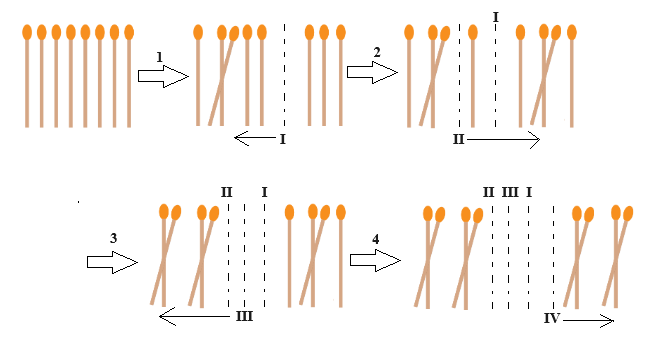
Figura 1: Uma estratégia vencedora do jogo, com q=8 palitos e saltos de tamanho t=2, em quatro movimentos
Fonte: Figura construída a partir do trabalho de Vignatti e Brito, 2014.
Observa-se que, nos primeiros dois passos, os dois saltos são sobre palitos individuais, enquanto nos dois últimos saltos, estes são dados sobre pares de palitos já formados.
A estratégia geral de sucesso, dado n natural positivo, com q=4n+4 palitos, e saltos de tamanho t=2n, é semelhante à usada acima. Essa estratégia consiste em deixar, inicialmente, npalitos individuais à esquerda do primeiro par formado, e npalitos individuais à direita do segundo par formado, após o primeiro par de saltos. Em seguida, vão se formando pares com os palitos individuais da ponta, de dentro para fora, de modo que os últimos pares formados são os das duas extremidades.
Observa-se na Figura 1, em que n=1, que, no primeiro par de movimentos, foi deixado n=1 palito individual à esquerda e n=1 palito individual à direita, conforme a estratégia vencedora descrita acima. E, em seguida, formou-se par com os palitos da ponta, concluindo o jogo. O trabalho de Cerqueira, Santos e Porto (2023) traz uma demonstração matemática de que essa estratégia é vencedora para qualquer quantidade q=4n+4 de palitos e saltos de tamanho t=2n.
Aplicação do jogo em sala de aula
Para a utilização do jogo em sala de aula com o objetivo de trabalhar o conteúdo de funções afins, a seguir será apresentada uma sequência de aplicação, incluindo os tempos estimados para cada passo. O tempo total previsto para a atividade é de aproximadamente 55 minutos.
- Apresentação do jogo e objetivo didático: O professor apresenta o jogo e seu propósito pedagógico para a turma, distribuindo 12 palitos para cada aluno ou grupo, conforme a decisão do docente sobre a realização da atividade de forma individual ou em grupos (tempo estimado: 5 minutos)
- Tentativa com 4 e 6 palitos: Os alunos são convidados a tentar concluir o jogo com 4 palitos, até perceberem que essa quantidade torna o jogo impossível. Em seguida, devem tentar com 6 palitos, constatando que, nesse caso, também não há solução. O mínimo necessário para que o jogo possa ser finalizado é de 8 palitos, conforme demonstrado por Cerqueira, Santos e Porto (2023). Não é necessário apresentar a demonstração matemática à turma (tempo estimado: 10 minutos).
- Tentativa com 8 palitos sem auxílio: Os alunos devem tentar finalizar o jogo com 8 palitos para que, sozinhos, possam estabelecer uma estratégia vencedora (tempo estimado: 10 minutos).
- Apresentação da estratégia: O professor apresenta a estratégia vencedora descrita neste artigo e permite que os alunos a reproduzam (tempo estimado: 10 minutos).
- Construção da função afim: O professor solicita aos alunos que construam a função afim f(x) na qual x=2 ou x=4 é a quantidade de pulos aos pares e f(x) é a quantidade de palitos individuais restantes entre os pares já formados após x saltos. Deseja-se que os alunos obtenham os coeficientes dessa função afim (tempo estimado: 10 minutos). Esse passo será explicado na sequência.
- Verificação da construção da função: O professor mostra no quadro a construção passo a passo da função f(x) estabelecida no passo 5 para os alunos, e verifica se algum estudante chegou na função afim corretamente, avaliando, assim, os alunos e a sua própria conduta na execução da aula (tempo estimado: 10 minutos). Fim da atividade.
Para o passo 4, o aluno, orientado pela Figura 1 (reproduzida na Figura 2 para melhor compreensão), deve considerar os seguintes valores da função:
- após x=2 saltos, observa-se que f(x)=f(2)=2 palitos individuais restam entre os pares formados;
- após x=4 saltos, observa-se que f(x)=f(4)=0 palitos individuais restam entre os pares formados.
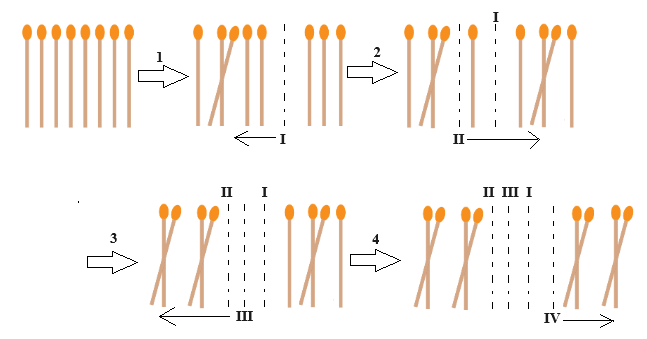
Figura 2: Visualização dos saltos para formação da função afim.
Fonte: Figura construída a partir do trabalho de Vignatti e Brito, 2014.
Ou seja, a função é tal que f(2)=2 e f(4)=0, com domínio={2, 4} e imagem={2, 0}.
Agora, o professor pode solicitar aos alunos que obtenham os coeficientes da função afim f(x)=ax+b. O seguinte sistema deve ser montado:
2a+b=2,
4a+b=0.
Assim, subtraindo a primeira da segunda, tem-se 2a=-2, a=-1. Logo, -2+b=2, b=4.
Enfim, f(x)=-x+4, domínio={2, 4} e imagem={2, 0}.
Verificação: f(2)=-2+4=2, f(4)=-4+4=0.
Concluídos os seis passos, caso haja mais tempo na aula ou na aula seguinte, o jogo pode ser proposto utilizando uma maior quantidade de palitos. A Figura 3 ilustra o jogo em que n=3, com q=4n+4=4.3+4=16 palitos e com saltos de tamanho t=2n=2.3=6:
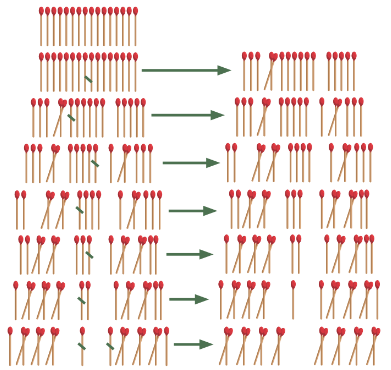
Figura 3: Realização do jogo com 16 palitos e saltos de tamanho 6.
Fonte: Figura retirada do artigo de Cerqueira, Santos e Porto, 2023.
Observa-se que, neste caso, a seguinte tabela de valores deve ser construída para a obtenção da função afim respectiva, sendo que serão necessários 8 saltos ao todo:
- f(2)=6 palitos centrais individuais entre os pares formados;
- f(4)=4 palitos centrais individuais entre os pares formados;
- f(6)=2 palitos centrais individuais entre os pares formados;
- f(8)=0 palitos centrais individuais entre os pares formados.
Domínio: {2, 4, 6, 8}. Imagem: {6, 4, 2, 0}.
Dessa forma, o aluno terá de montar a função afim f(x)=ax+b tal que f(2)=6 e f(4)=4, por exemplo. Ou seja,
2a+b=6,
4a+b=4.
Subtraindo a primeira da segunda, tem-se 2a=-2, a=-1. Desta forma, -2+b=6, b=8.
Logo, f(x)=-x+8. Verificação:
f(2)=-2+8=6,
f(4)=-4+8=4,
f(6)=-6+8=2 e
f(8)=-8+8=0.
Já com 12 palitos, o jogo é tal que 4n+4=12, isto é, n=2. Dessa forma, os saltos são de tamanho 2n=4. E assim sucessivamente. Cada n natural positivo enseja um jogo com 4n+4 palitos e saltos de tamanho 2n, e cada variação dessas fornece uma função afim diferente, cuja construção pode ser proposta aos alunos.
É interessante notar que outras funções afins podem ser criadas a partir do jogo dos palitos, como por exemplo:
- a função g(q) que dá a quantidade de saltos necessários, em função da quantidade q de palitos. No caso de q=8 palitos (n=1), observando a figura 2, nota-se que 4 saltos são necessários para se formarem todos os pares, isto é, g(8)=4. Para q=12 palitos (n=2), 6 saltos são necessários para se formarem os 6 pares de palitos. Para q=16 palitos (n=3), 8 saltos, como ilustra a figura 3. Logo, g(q)=q/2. Domínio={8,12,16,...} e imagem={4,6,8,...}.
- a função h(x) que dá a quantidade de palitos individuais, em função de x saltos, x=2,4,... aos pares, que restam à direita do último par formado. Assim, com 8 palitos, observando a figura 2, tem-se f(2)=1 e f(4)=0, sendo, portanto, 2a+b=1 e 4a+b=0, isto é, b=-4a, 2a-4a=1, a=-½ e b=2, portanto, h(x)=-x/2+2. Domínio={2,4} e imagem={1,0}. Já com 16 palitos, observando a figura 3, tem-se h(2)=3, h(4)=2, h(6)=1 e h(8)=0. Logo, 2a+b=3 e 4a+b=2. Subtraindo, 2a=-1, a=-½ e b=4 e, portanto, h(x)=-x/2+4. Domínio={2,4,6,8} e imagem={3,2,1,0}.
Percebe-se, dessa forma, que o jogo dos palitos pode proporcionar uma variedade significativa de funções afins distintas para serem exploradas em sala de aula de maneira lúdica. Caso não haja palitos disponíveis, cartas de baralho podem ser utilizadas como alternativa.
Conclusões
Conclui-se que o jogo dos palitos pode ser bastante útil nas aulas de Matemática da Educação Básica, tornando essas aulas versáteis e inovadoras. Por se tratar de uma atividade lúdica de manipulação, o jogo tem o poder de capturar a atenção dos estudantes. Além disso, ao associar o jogo ao tema das funções, é possível que os alunos, movidos pelo interesse e curiosidade, compreendam de forma mais efetiva e divertida esse conteúdo.
O jogo dos palitos permite trabalhar o conceito de funções polinomiais do primeiro grau, domínio e imagem de funções. O professor pode fornecer diversas funções distintas, todas afins, dependendo da quantidade de palitos utilizados e dos respectivos tamanhos dos saltos, e dependendo também de qual grandeza está sendo observada: seja a quantidade de palitos individuais centrais restantes após x saltos, seja a quantidade de palitos individuais restantes à direita da última dupla de palitos formada após x passos, ou seja a quantidade de movimentos totais necessários para a conclusão satisfatória do jogo, que depende da quantidade de palitos. Cada uma dessas funções afins possui seu domínio, imagem e coeficientes angular e linear, que devem ser encontrados pelos alunos, após a execução das atividades orientadas pelo professor.
O jogo pode ser aplicado em atividades sobre funções para diferentes públicos, pois pode ser utilizado tanto para iniciar o estudo de funções polinomiais do primeiro grau quanto para reforçar conceitos desses temas, que são abordados em todos os anos a partir do nono ano do Ensino Fundamental até o terceiro ano do Ensino Médio, e até mesmo em disciplinas de Matemática Básica do Ensino Superior. Nesse contexto, o professor universitário pode empregar o jogo para que os estudantes relembrem o conceito de funções.
Caso haja tempo para atividades além das apresentadas nesse artigo, o professor pode ainda revelar que o jogo com 8 palitos e saltos de tamanho 2 pode ser concluído também com qualquer quantidade q de palitos acima de 8, com q par e salto de tamanho fixo em 2. Ele pode sugerir aos estudantes que tentem uma estratégia vencedora com 10 palitos e depois com 12 palitos, com tamanho fixado do salto igual a 2 para ambos os casos. Após as tentativas, o professor pode revelar a estratégia vencedora, que consiste em, primeiramente, fazer par com algum palito da extremidade, seja a extremidade da esquerda, seja da direita; assim, esse par não será mexido e o problema se reduzirá a q-2 palitos. Se for com 10 palitos, o problema se reduzirá a 8 palitos após o primeiro par formado com um dos palitos de qualquer uma das extremidades. Já com 12 palitos, o problema se reduzirá à 10, que, posteriormente, se reduzirá à 8, cuja solução já é conhecida. Dessa forma, o jogo dos palitos se mostra muito rico quando se pensa nas possibilidades de aplicação ao ensino de Matemática, em particular, de funções afins.
Referências
AZEVEDO, Kleber Tuxen Carneiro. Por uma memória do jogo: a presença do jogo na infância de octogenários e nonagenários. 2015. 260f. Tese (Doutorado) – Faculdade de Ciências e Letras, Universidade Estadual Paulista Júlio de Mesquita Filho, Araraquara, 2015.
BOOTH, R. L. Dificuldades das crianças que se iniciam em álgebra. In: COXFORD, A. F.; SHULTE, A. P. (ed.). As ideias da Álgebra. São Paulo: Atual, 1995. p. 23-37.
BRASIL. MEC. Base Nacional Curricular Comum (BNCC). Brasília: MEC, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 30 out. 2023.
CERQUEIRA, Elisângela Fernandes; SANTOS, Rogério César; PORTO, Katarina Silva. O Teorema dos Palitos Saltitantes. Revista Professor de Matemática, Rio de Janeiro, v. 106, 2023.
CIRÍACO, Flávia Lima. Utilizando jogos para ensinar Matemática. Revista Educação Pública, Rio de Janeiro, v. 22, nº 34, 13 set. 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/34/utilizando-jogos-para-ensinar-matematica. Acesso em: 30 out. 2023.
FIORENTINI, D.; MIORIM, M. A. Uma reflexão sobre o uso de materiais concretos e jogos no ensino da Matemática. Boletim da SBEM, São Paulo, ano 4, nº 7, 1990.
LIMA, Elon Lages. Números e funções reais. Rio de Janeiro: SBM, 2013. Coleção Profmat.
RADFORD, L. Some reflections on teaching algebra through generalization. In: BEDNARZ, N.; KIERAN, C.; LEE, L. (eds.). Approaches to algebra. Dordrecht: Kluwer, 1996. p. 107-111.
SMOLE, K. S.; DINIZ, M. I.; CÂNDIDO, P. Jogos de matemática de 1º a 5º ano. Porto Alegre: Artmed, 2007. Série Cadernos do Mathema – Ensino Fundamental.
URSINI, S.; TRIGUEROS, M. La conceptualización de la variable en la enseñanza media. Educación Matemática, México, v. 12, nº 2, p. 27-48, 2000.
VIGNATTI, A.; BRITO, P. F. Jogos de palito e indução finita. Revista Professor de Matemática, Rio de Janeiro, v. 84, 2014.
Publicado em 15 de janeiro de 2025
Como citar este artigo (ABNT)
SANTOS, Rogério César dos; BEZERRA, Wescley Well Vicente. Explorando funções afins a partir do jogo dos palitos. Revista Educação Pública, Rio de Janeiro, v. 25, nº 2, 15 de janeiro de 2025. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/25/2/explorando-funcoes-afins-a-partir-do-jogo-dos-palitos
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

